シグモイド関数の数理

「シグモイド関数」は科学的に重要な関数の一つであり、入試問題の題材としてもよく見かけるが、高校（大学も？）においてその具体的な性質について学ぶ機会はあまり無いと思われる。或いは、そのような関数を目にしていても、それがシグモイドと呼ばれているとは知らない人も居るかもしれない。そこで本稿ではシグモイド関数の性質について解説していくことにする。

---

「シグモイド」という語

大学入試問題にシグモイド関数が登場していても、それに気付かない（存在を知らなければ「気付けない」）学生は多いと思われる。また、エンジニアなどの方であれば、人工知能の分野に触れて初めてシグモイド関数の存在を知ったという人も多いのではないだろうか。

シグモイド関数$$\varsigma(x)=\dfrac{1}{1+e^{-x}}$$はニューラルネットワークの活性化関数として用いられることの多い関数であり、エンジニアにとっては比較的馴染みのある関数であろう。

生化学の分野でもアロステリックタンパク質や酵素の活性を論じる際の飽和曲線として登場し、また医学や環境工学などにおいて用量反応関係を説明する数式にシグモイド関数が現れることも珍しくない。

酸素とヘモグロビンの結合に関する協同効果を説明する経験式として知られる「ヒルの式」(Hill equation)や、個体群成長モデルを記述する関数の一つとして知られる「ロジスティック関数」などの「S字型」の関数はすべて「シグモイド型」の関数であり、シグモイド曲線に属する。

「シグモイド」という言葉の意味は嚙み砕いて言えば「シグマっぽい」という意味合いのもので、曲線の形がギリシャ文字の「シグマ」に似ていることから、そのように呼ばれている。ただしシグマといっても$\sigma$の方ではなく、語末形の$\varsigma$に由来している。

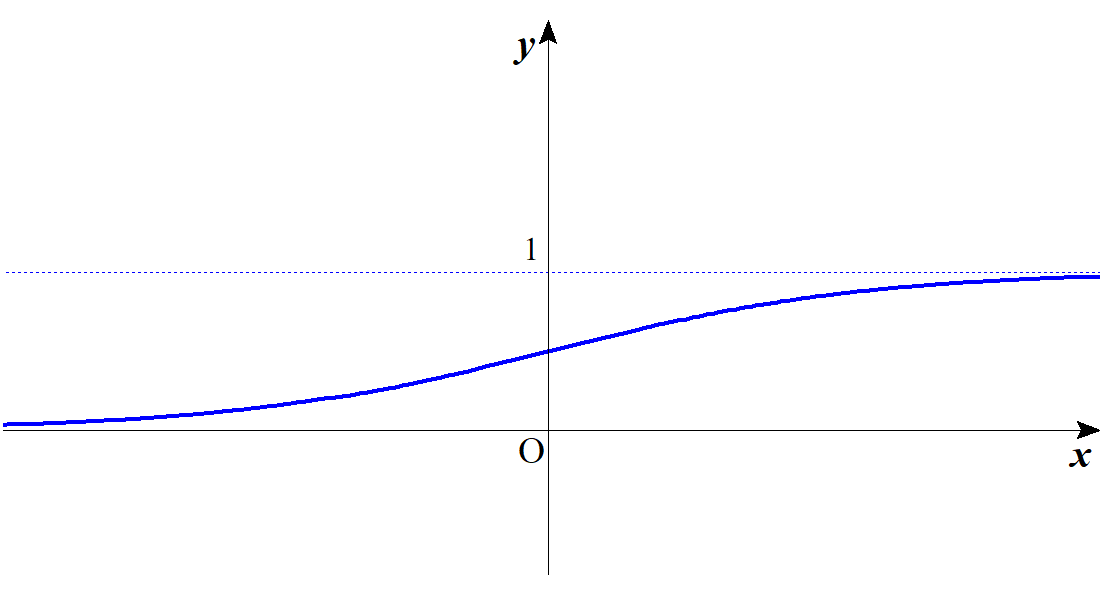
以下に $y=\varsigma(x)$ のグラフを示す。やや扁平ではあるが、S字型の関数であることが分かるだろう。

---

$\varsigma(x)$の基本的な性質

冒頭で示した形の関数$$\varsigma(x)=\dfrac{1}{1+e^{-x}}\tag{1}$$は「標準シグモイド関数」と呼ばれており、より一般に「シグモイド関数」と言えば$$\varsigma_a(x)=\dfrac{1}{1+e^{-ax}}\tag{2}$$という形の関数群を指す。標準シグモイド関数とは、一般のシグモイド関数において $a=1$ とした特殊な場合と言える。

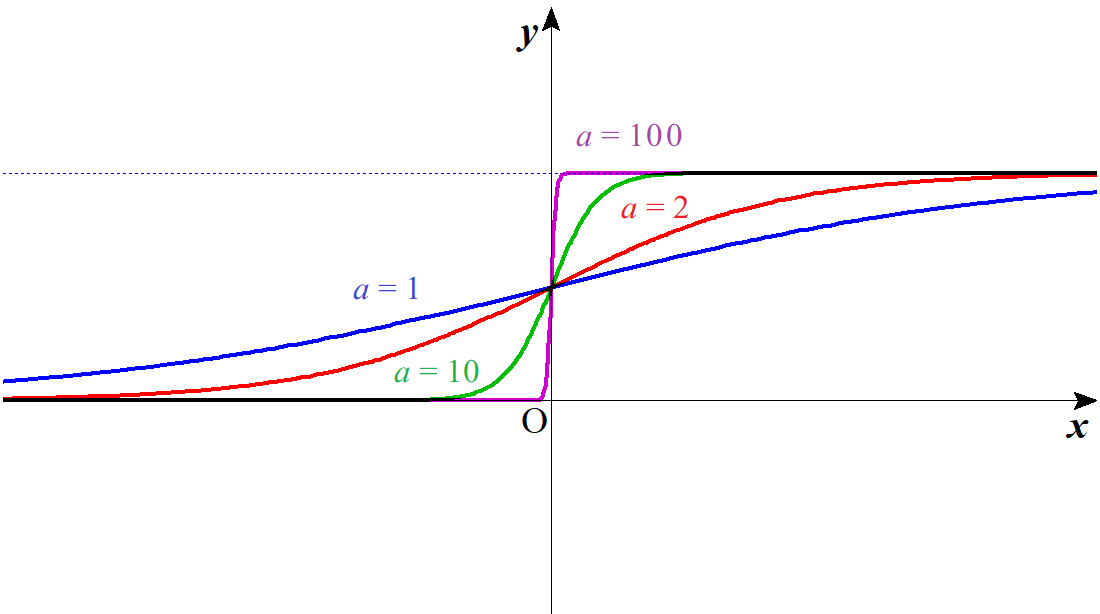
シグモイド関数を係数$a$を変化させながら描くと以下のようになる。

これを見て分かる通り、シグモイド関数は単調増加で変曲点は $\left(0,\,\dfrac{1}{2}\right)$ にのみ存在する。シグモイド関数は変曲点に関して点対称であり、$\varsigma_a(x)-\dfrac{1}{2}$ は奇関数なので$$\varsigma_a(-x)=1-\varsigma_a(x)\tag{3}$$という関係式が成立する。

係数$a$を大きくしていくと曲線のS字の曲り方は次第に直角に近付いていき、$a$を無限大にするとほとんどヘヴィサイド関数（※注）のような形となる。

※注：ヘヴィサイド関数$H(x)$は正の引数に対して$1$を、負の引数に対して$0$を返す階段関数の一種である。具体的に書き表すと、$$H(x)=\begin{cases} 1\ \ \ (x>0) \\ 0 \ \ \ (x<0) \end{cases}$$となる。

また、$\varsigma_a(x)$ は双曲線正接関数 $\tanh x=\dfrac{e^{x}-e^{-x}}{e^{x}+e^{-x}}$ によって$$\varsigma_a(x)=\dfrac{1}{2}\left(\tanh \dfrac{ax}{2}+1\right)\tag{4}$$と表すことができる。

---

$\varsigma(x)$の逆関数

係数$a$は「ゲイン」（gain）と呼ばれるが、これは恐らくシグモイド関数の逆関数に関連する用語と思われる。シグモイド関数 $y=\dfrac{1}{1+e^{-ax}}$ を$x$について解けば、$$x=-\dfrac{1}{a}\log\left(\dfrac{1-y}{y}\right)$$となるので、シグモイド関数の逆関数$\varsigma_a^{-1}(x)$は$$\varsigma_a^{-1}(x)=\dfrac{1}{a}\log\left(\dfrac{x}{1-x}\right)\tag{5}$$と求められる。ここで$\log\left(\dfrac{x}{1-x}\right)$には「ロジット関数」という名前が付いている。ロジット関数は $0<x<1$ の範囲で定義される関数で、$\text{logit}(x)$と表記される。ロジット関数は確率論における「オッズ」（odds）に対数をとったものと解釈でき、統計学や心理学にも応用される関数である。$\dfrac{x}{1-x}$は$x$を「ある事象$A$が起こる確率」と読み替えれば、$A$が起こる確率と$A$が起こらない確率の比になっていることが理解できるだろう。オッズは賭け率とも呼ばれ、事象$A$が「ギャンブルに勝つこと」だとすると、そのギャンブルがどれだけの勝率であるかの指標となる。単純化されたギャンブルなどはロジスティック回帰の適当なモデルとなる。

---

$\varsigma(x)$の導関数

シグモイド関数$\varsigma_a(x)$を$x$について微分すると$$\varsigma_a^{\,\prime}(x)=\dfrac{ae^{-ax}}{(1+e^{-ax})^2}\tag{6}$$となり、これは元の$\varsigma_a(x)$を用いて$$\varsigma_a^{\,\prime}(x)=a\varsigma_a(x)\{1-\varsigma_a(x)\}\tag{7}$$と表せる。途中の式変形はそれほど難しくないので、まずは各自で確認して頂きたい。

また、二次導関数は$(7)$式を微分すればよいだけなので、$$\varsigma_a^{\prime\prime}(x)=a^2\varsigma_a(x)\{1-\varsigma_a(x)\}\{1-2\varsigma_a(x)\}\tag{8}$$と表せる。

このように導関数が元の関数を用いて再帰的に表現できるため、プログラミングと相性が良い場合がある。この関係式の存在が、深層学習においてシグモイド関数が活性化関数として利用されている所以である。

因みに三次導関数はあまりすっきりした式にはならず、$$\varsigma_a^{\prime\prime\prime}(x)=a^3\varsigma_a(x)\{1-\varsigma_a(x)\}\{1-6\varsigma_a(x)+6\varsigma_a^2(x)\}\tag{9}$$となるが、再帰的に表記することは一応可能である。

また、$\varsigma_a(x)$に対数をとった関数の導関数も、以下のように再帰的に表せることが知られている。

$$\dfrac{d}{dx}\log\varsigma_a(x)=a\varsigma_a(-x)=a\{1-\varsigma_a(x)\}\tag{10}$$

---

$\varsigma(x)$の積分

$$\begin{align}&\ \ \ \ \displaystyle \int \dfrac{dx}{1+e^{-ax}} \\ &=\displaystyle \int \dfrac{e^{ax}}{1+e^{ax}}dx \\ &=\int \left(\dfrac{(1+e^{ax})’}{1+e^{ax}}\right)dx \\ &=\dfrac{1}{a}\log(1+e^{ax})+C \end{align}$$となり、$$\begin{align}&\ \ \ \ \log(1+e^{ax}) \\ &=-\log\left(\dfrac{1}{1+e^{ax}}\right) \\ &=-\log\left(\dfrac{e^{-ax}}{1+e^{-ax}}\right) \\ &=-\log\left(1-\dfrac{1}{1+e^{-ax}}\right) \\ &=-\log(1-\varsigma_a(x)) \end{align}$$となるので、シグモイド関数の積分は$$\displaystyle \int \varsigma_a(x) dx = -\dfrac{1}{a}\log(1-\varsigma_a(x))+C$$と求められる。これより、$y=1$ と $y=\varsigma_a(x)$ 及び$y$軸で囲まれた部分の面積は、広義積分の知識を使うことにより $\dfrac{1}{a}\log 2$ であることが分かる（$y=\varsigma_a(x)$ 及び$x$軸、$y$軸で囲まれた部分の面積も同様）。

このように、シグモイド関数の原始関数もまた導関数と同様に、再帰的に表現できる。

---

---

シグモイドに関する入試問題

それでは折角なのでシグモイドを題材とした入試問題を１問だけ示しておこう。2017年の横浜市立大の小問にシグモイドの導関数に関する至ってシンプルな出題がある。

---

《問題》

関数$f(x)$を$$y=\dfrac{1}{1+e^{-x}}$$とする。このとき、導関数$f^{\prime}(x)$の最大値を求めよ。

---

さて、シグモイドの導関数はいわゆる「ガウシアン型」の関数となり、必ず最大値をもつ。これはシグモイドの接線の傾きが変曲点において最大となることを意味している。

関数 $y=f(x)$ を微分すると、$$\begin{align} \dfrac{dy}{dx} &=\dfrac{d}{dx}\left(\dfrac{1}{1+e^{-x}}\right) \\ &=\dfrac{d}{dx}(1+e^{-x})^{-1} \\ &=-(1+e^{-x})'(1+e^{-x})^{-2} \\ &=\dfrac{e^{-x}}{(1+e^{-x})^{2}} \end{align}$$となる。ここで$$\begin{align} \dfrac{e^{-x}}{(1+e^{-x})^{2}} &= \dfrac{e^{-x}}{1+e^{-2x}+2e^{-x}} \\ &=\dfrac{1}{e^{x}+e^{-x}+2} \end{align}$$と変形できることを利用すれば、分母について相加相乗平均の不等関係が利用でき、$$e^{x}+e^{-x} \geqq 2 \sqrt{e^{x} \cdot e^{-x}}=2$$（等号成立は $x=0$）が成り立つので、$$\begin{align} f^{\prime}(x) &=\dfrac{1}{e^{x}+e^{-x}+2} \\ &\leqq \dfrac{1}{2+2} \\ &= \dfrac{1}{4} \end{align}$$となる。故に導関数$f^{\prime}(x)$の最大値は $\dfrac{1}{4}$ と求められる。

---

この問題は相加相乗平均の不等式が利用できるところがポイントである。勿論、更に微分しても良いのだが、計算はより煩雑になってしまう。

本問は非常に易しい部類の問題であるが、他にもシグモイド関数が題材となっている入試問題はちらほら見掛ける。試験対策というほどでもないが、問題を見たときに予備知識があると何かと見通しが良くなることがある。これを機にシグモイド関数を知って頂ければ幸いである。