前回の記事で扱った各位の数字にゼロが現れない数 “zeroless number” から派生する話題です。
zeroless数
各位の数字にゼロが現れない数を「zeroless数」と呼ぶことにします。特に断りの無い限り十進法表記の場合について考えます。例えば $1234$ はzeroless数で、$1024$ は非zeroless数です。
前回のエントリで紹介しましたが、$k^n$（$k \in \mathbb{N}$、$n \in \mathbb{N}$）の十進展開にゼロが現れないような$n$には最大値が存在することが予想されています。例えば $k=2$ の場合、$2^n$をzeroless数にするような$n$で$86$より大きなものは存在しない（最大値が$86$である）と予想されています。厳密には証明されていないので、あくまでも予想（未解決問題）です。
また、フィボナッチ数列$\{F_n\}$についても、第184項$F_{184}$がzeroless数となる最大のフィボナッチ数と予想されています。このようにzeroless数が頭打ちになる現象は、項番号が大きくなるほど桁数が増加するため、0～9のどの数字も均等に出現するようになることが理由だと考えられます。
そこで、0～9が実際に各位の数字として均等に出現しているか否かが気になります。
各位の数字のランダム性
$2^n$の各位の数字に0～9の10種類の数字が何個出現するかを「2^nの各位の数字の個数一覧」のページにまとめています。フィボナッチ数列$\{F_n\}$については「フィボナッチ数の各位の数字の個数一覧」のページにまとめています。（いずれのページもデータ量が非常に大きいので閲覧の際は注意して下さい）
これらのデータから、$n$が増大するにつれて$2^n$や$F_n$の各位には0～9の数字がほぼ均等に出現することが分かります。試しに、$0$の出現個数を桁数で割った値をプロットしてみると次のようになります。
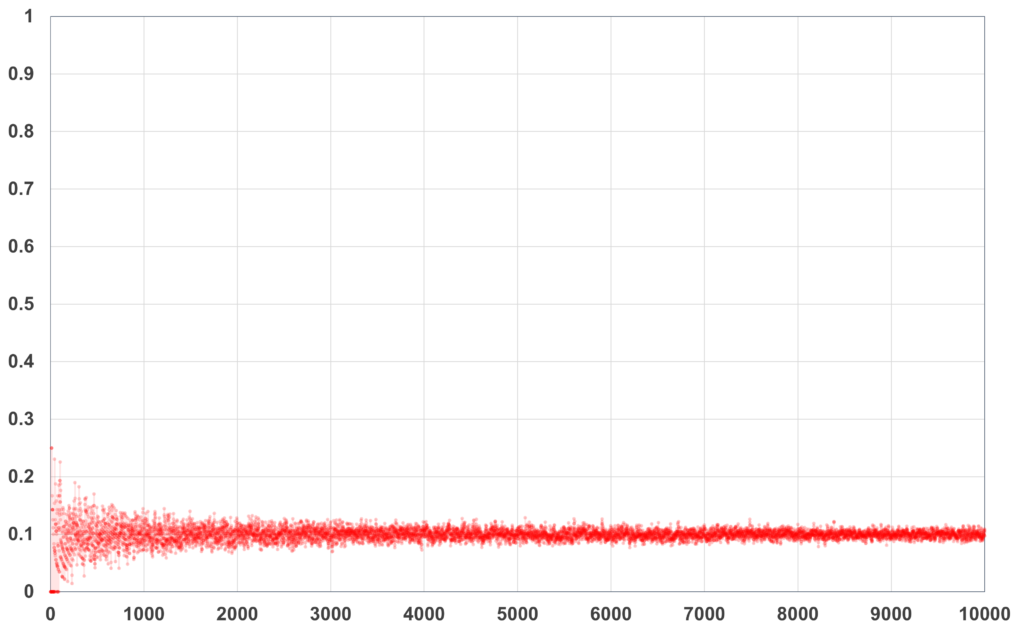図．$2^n$の各位に現れる「0」の個数$\div$桁数
（横軸は項番号$n$）
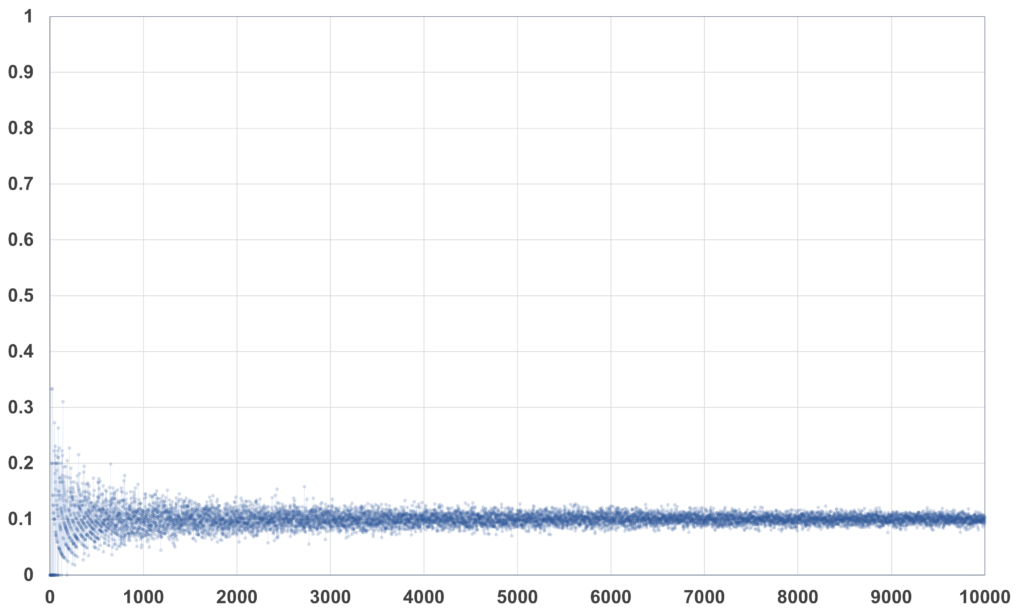図．フィボナッチ数$F_n$の各位に現れる「0」の個数$\div$桁数
（横軸は項番号$n$）
どちらも$0.1$に収束しているように見えます。実際に「0」以外の数字に対してプロットしてみても同じような結果が得られます。
各位の数字が0～9の10種類の数から均等に選ばれるとすれば、縦軸の値は$0.1$に近付くはずです。言い換えれば、縦軸の値が$0.1$付近になるということは各位の数字として0～9が均等に現れていることになります。
ただ、完全にランダムな配列になっているのかどうかを厳密に判定するのは（可能かもしれませんが）難しそうです。
※ここでは各数字が各位の数字として均等な割合で出現することを「ランダム」と表現しています。
その他の記数法の場合
$2^n$の各位の数字には0～9の10種類の数がほぼ均等に現れることが分かりましたが、10進法以外の記数法についても同様のことが成り立つのでしょうか？
3～10進法の場合について、$2^n$の各位の数字の個数をプロットすると次のようになります。0～9のそれぞれについて色分けし、$1 \leqq n \leqq 5000$ の範囲でカウントしています。
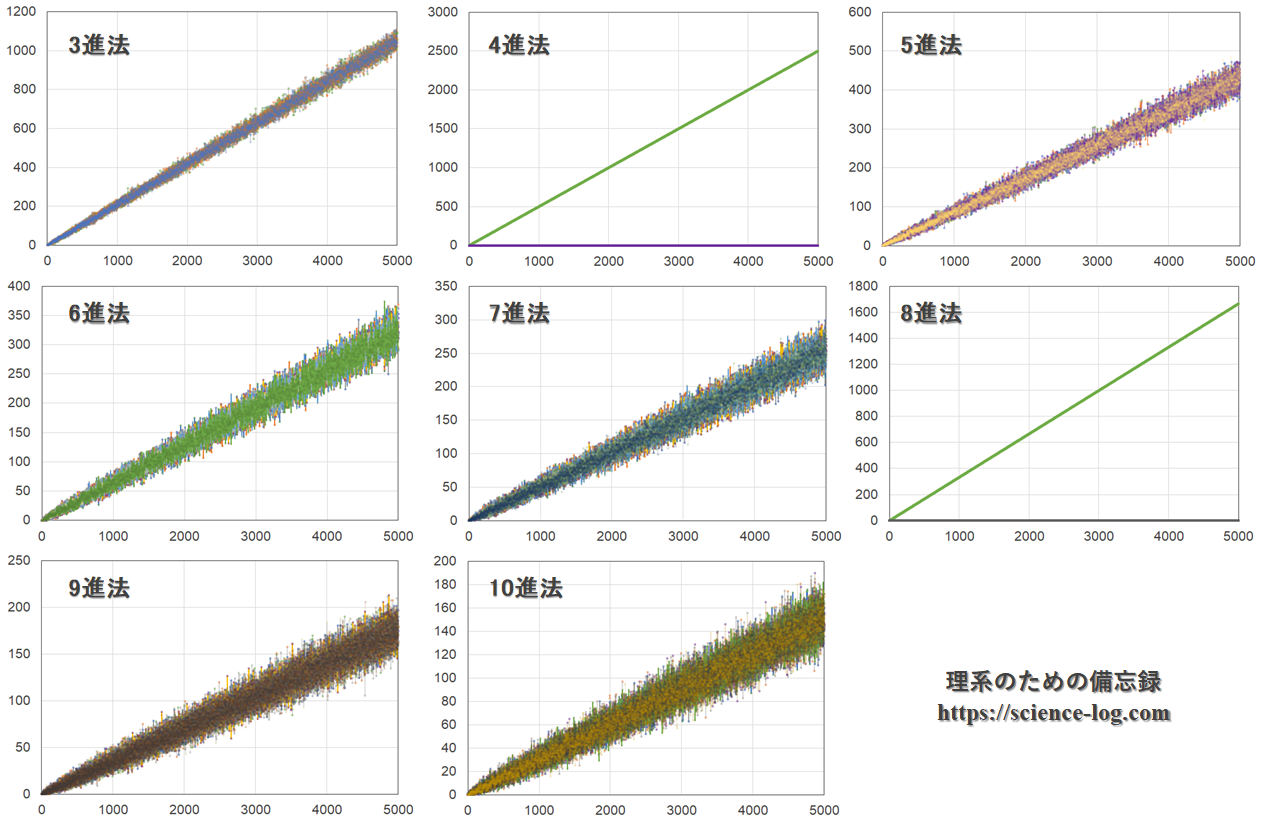図．$2^n$の各位に現れる数字の個数
（横軸は項番号$n$）
2のべき乗なので4進法や8進法ではつまらないグラフになっていますが、それ以外の記数法においては、どの数字もおおむね均等に出現しているようです。
基数が大きくなるほど折れ線の振れ幅が大きくなっているように見えますが、これは自然な現象なのでしょうか？ 何となくフラクタル構造が隠れているようにも見えます。
zero以外の場合
以上のことを踏まえれば、zeroless数に限らず “one-less数” や “two-less数” などについても同様に最大値が存在するであろうことは感覚的に理解できます。
少し調べてみると、$2^n$のone-less数は次の26個で全部のようです。
one-less数（26個）
$2^{1} = 2$
$2^{2} = 4$
$2^{3} = 8$
$2^{5} = 32$
$2^{6} = 64$
$2^{8} = 256$
$2^{11} = 2048$
$2^{12} = 4096$
$2^{15} = 32768$
$2^{16} = 65536$
$2^{19} = 524288$
$2^{23} = 8388608$
$2^{25} = 33554432$
$2^{28} = 268435456$
$2^{32} = 4294967296$
$2^{33} = 8589934592$
$2^{35} = 34359738368$
$2^{38} = 274877906944$
$2^{43} = 8796093022208$
$2^{52} = 4503599627370496$
$2^{56} = 72057594037927936$
$2^{59} = 576460752303423488$
$2^{63} = 9223372036854775808$
$2^{66} = 73786976294838206464$
$2^{73} = 9444732965739290427392$
$2^{91} = 2475880078570760549798248448$
以下、同様に調べてみます。（指数部分のみ）
two-less数（22個）
2, 3, 4, 6, 12, 14, 16, 20, 22, 23, 26, 34, 35, 36, 39, 42, 46, 54, 64, 74, 83, 168
three-less数（33個）
1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12, 13, 18, 19, 20, 21, 24, 26, 32, 34, 38, 40, 44, 48, 50, 53, 57, 60, 80, 91, 92, 102, 153
four-less数（23個）
1, 3, 4, 5, 7, 8, 9, 13, 15, 16, 17, 21, 23, 24, 29, 40, 41, 43, 55, 69, 75, 85, 107
five-less数（33個）
1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13, 14, 15, 17, 18, 22, 23, 24, 26, 27, 30, 31, 32, 34, 36, 38, 43, 46, 55, 62, 65, 66, 71
six-less数（27個）
1, 2, 3, 5, 7, 9, 10, 11, 13, 17, 19, 21, 22, 25, 27, 30, 33, 37, 39, 41, 45, 47, 53, 54, 57, 90, 93
seven-less数（29個）
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 16, 18, 19, 22, 23, 25, 28, 33, 41, 42, 49, 50, 54, 61, 71
eight-less数（25個）
1, 2, 4, 5, 6, 8, 9, 10, 12, 16, 17, 18, 21, 22, 24, 25, 32, 40, 41, 49, 52, 53, 56, 73, 78
nine-less数（36個）
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 14, 15, 16, 17, 18, 19, 20, 23, 24, 25, 26, 27, 28, 30, 31, 45, 46, 47, 57, 58, 59, 71, 77, 99, 108
これらは$2^n$を10進法で表した場合の指数ですが、$3^n$など他の累乗数についても○○-less数は有限個に限られ、10進法以外の記数法においても○○-less数は有限個しか存在しないと予想されます。
※ただし、$2^n$の4進数表記などの自明な場合を除きます。
この辺りの話題に詳しい方は是非コメントして頂けると幸いです。