ネイピア数eの値を評価する（横浜市立大学2010年理系数学第4問）

解答例

（１）

$y=e^x$ に対して$$y^{\prime }=e^x,y^{\prime \prime }=e^x$$となるから $y^{\prime \prime }>0$ であり $y=e^x$ のグラフは下に凸である。

したがって、この曲線上に2点 $A(a,e^a)$、$B(0,1)$ をとると、

(ⅰ) $B$における曲線の接線は、$B$を除き曲線より下側にあり、

(ⅱ) 線分$AB$は両端を除き曲線より上側にある。

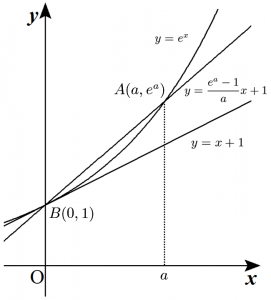
ここで、点$B$における接線の方程式は$$y=x+1$$であり、直線$AB$の方程式は$$y={\displaystyle \frac{e^a-1}{a}}x+1$$である。よって $0\leqq x\leqq a$ をみたす$x$に対して不等式$$1+x\leqq e^x\leqq 1+{\displaystyle \frac{e^a-1}{a}}x$$が成り立つ。

□

（２）

（１）の不等式は $0<x<a$ では等号が成り立たないことに注意すると、各辺を積分して$$\begin{array}{c}{\displaystyle {\int }_0^a(1+x)dx<{\int }_0^a{e}^{x}dx<{\int }_0^a(1+{\displaystyle \frac{e^a-1}{a}}x)dx}\\ \therefore {[x+{\displaystyle \frac{x^2}{2}}]}_0^a<{\left[e^x\right]}_0^a<{[x+{\displaystyle \frac{e^a-1}{2a}}{x}^2]}_0^a\\ \therefore a+{\displaystyle \frac{a^2}{2}}<e^a-1<a+{\displaystyle \frac{a}{2}}(e^a-1)\\ \therefore 1+a+{\displaystyle \frac{a^2}{2}}<e^a<1+{\displaystyle \frac{a}{2}}(e^a+1)\end{array}$$と示される。

□

（１）（別解）

$$\begin{array}{l}f(x)=e^x-(1+x)\\ g(x)=(1+{\displaystyle \frac{e^a-1}{a}}x)-e^x\end{array}$$と置く。
$$f^{\prime }(x)=e^x-1$$より、$f(x)$の増減は次のようになる。$$\begin{array}{|cccc|}\hline x& \cdots & 0& \cdots \\ f^{\prime }(x)& –& 0& +\\ f(x)& <img\; draggable="false"\; role="img"\; class="emoji"\; alt="\searrow "\; src="https://s.w.org/images/core/emoji/15.0.3/svg/2198.svg">& 0& <img\; draggable="false"\; role="img"\; class="emoji"\; alt="\nearrow "\; src="https://s.w.org/images/core/emoji/15.0.3/svg/2197.svg">\\ \hline\end{array}$$よって $f(x)\geqq 0\cdots \mathrm{①}$ となる。等号成立は $x=0$ のとき。

また、$$g^{\prime }(x)=\frac{e^a-1}{a}-e^x$$であり、これは単調減少である。ここで、$$\begin{array}{rl}{g}^{\prime }(0)& ={\displaystyle \frac{e^a-1}{a}}-1\\ & ={\displaystyle \frac{1}{a}}(e^a-1-a)\end{array}$$ $$\begin{array}{rl}{g}^{\prime }(a)& ={\displaystyle \frac{e^a-1}{a}}-e^a\\ & ={\displaystyle \frac{e^a}{a}}(1-e^{-a}-a)\end{array}$$となる。①より、$$\begin{array}{l}{g}^{\prime }(0)={\displaystyle \frac{1}{a}}f(a)>0\\ g^{\prime }(a)=-{\displaystyle \frac{e^a}{a}}f(-a)<0\end{array}$$これらと$g^{\prime }(x)$が単調減少であることから、$g^{\prime }(x)=0$ となる$x$が $0<2<a$ に１つだけ存在し、その値をとすると $g(x)$ の増減は次のようになる。$$\begin{array}{|cccccc|}\hline x& 0& \cdots & x_0& \cdots & a\\ g^{\prime }(x)& & +& 0& –& \\ g(x)& 0& <img\; draggable="false"\; role="img"\; class="emoji"\; alt="\nearrow "\; src="https://s.w.org/images/core/emoji/15.0.3/svg/2197.svg">& & <img\; draggable="false"\; role="img"\; class="emoji"\; alt="\searrow "\; src="https://s.w.org/images/core/emoji/15.0.3/svg/2198.svg">& 0\\ \hline\end{array}$$これより $0\leqq x\leqq a$ において $g(x)\geqq 0$ となる。よって $0\leqq x\leqq a$ において不等式$$1+x\leqq e^x\leqq 1+{\displaystyle \frac{e^a-1}{a}}x$$が成り立つ。

□

（２）（別解）

$$\begin{array}{l}F(x)=e^x-(1+x+{\displaystyle \frac{x^2}{2}})\\ G(x)=\{1+{\displaystyle \frac{x}{2}}(e^x+1)\}-e^x\end{array}$$と置くと、$$\begin{array}{rl}{F}^{\prime }(x)& =e^x-(1+x)\\ & =f(x)\\ G^{\prime }(x)& =\frac{1}{2}(e^x+1)+\frac{x}{2}{e}^x-e^x\\ & =\frac{e^x}{2}(-1+e^{-x}+x)\\ & =\frac{e^x}{2}f(-x)\end{array}$$よって（１）の別解の結果から $F^{\prime }(x)\geqq 0$ かつ $G^{\prime }(x)\geqq 0$ となる。等号は $x=0$ のときにのみ成立し、$F(x)$と$G(x)$はともに単調増加である。したがって$$\{\begin{array}{l}F(a)>F(0)=0\\ G(a)>G(0)=0\end{array}$$が言えるから$$1+a+{\displaystyle \frac{a^2}{2}}<e^a<1+{\displaystyle \frac{a}{2}}(e^a+1)$$の成立が示される。

□

（３）

（２）の不等式に $a={\displaystyle \frac{1}{2}}$ を代入すると$$1+\frac{1}{2}+\frac{1}{8}<e^{\frac{1}{2}}<1+\frac{1}{4}(e^{\frac{1}{2}}+1)$$ $$\therefore \frac{13}{8}<e^{\frac{1}{2}}<\frac{5}{3}$$この各辺は正なので二乗して、$$\frac{169}{64}<e<\frac{25}{9}$$を得る。ここで、${\displaystyle \frac{169}{64}}=2.640\dots$、${\displaystyle \frac{25}{9}}=2.777\dots$ より、$$2.64<e<2.78$$が示される。

□