本稿では「フィボナッチ数列の加法定理」について解説します。
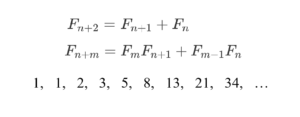
フィボナッチ数列とは
「フィボナッチ数列」とは、初項が $F_1=1$、$F_2=1$ であり$$F_{n+2}=F_{n+1}+F_{n}$$という漸化式で与えられる数列の名前です。各項を書き下すと、
1, 1, 2, 3, 5, 8, 13, 21, 34, …
と続きます。黄金比との関係から自然界に現れることも多く(※注)、これまで数多くの数学者によって研究されてきた世界で最も有名な数列の一つです。
フィボナッチ数列の一般項は$$\small F_{n}=\frac{1}{\sqrt{5}}\left(\frac{1+\sqrt{5}}{2}\right)^{n}-\frac{1}{\sqrt{5}}\left(\frac{1-\sqrt{5}}{2}\right)^{n}$$で与えられます。ここで黄金比$$\varphi = \dfrac {1+ {\sqrt {5}}} {2} \approx 1.61803 \ldots$$を用いれば$$F_{n}=\frac{\varphi^{n}-(-\varphi)^{-n}}{\sqrt{5}}$$という非常に簡潔な式で与えることができます。
漸化式の代わりに行列を使って$$\left(\begin{array}{ll}
1 & 1 \\
1 & 0
\end{array}\right)^{n}=\left(\begin{array}{cc}
F_{n+1} & F_{n} \\
F_{n} & F_{n-1}
\end{array}\right)$$と表すこともできます。
(※注) フィボナッチ数は花びらの数に現れることが多く、パイナップルや松ぼっくり、ひまわりの種の螺旋などにも現れます。
一般フィボナッチ数列と加法定理
初項$G_1$、$G_2$をある整数として、$$G_{n+2}=G_{n+1}+G_{n}$$という漸化式で与えられる「一般フィボナッチ数列$\{G_n\}$」(generalized Fibonacci sequence)というものを考えてみます。
このとき$$\small \begin{aligned}
G_{n+3} &=G_{n+2}+G_{n+1} \\
&=\left(G_{n+1}+G_{n}\right)+G_{n+1} \\
&=\color{red}{2 G_{n+1}+G_{n}} \\
G_{n+4} &=G_{n+3}+G_{n+2} \\
&=\left(2 G_{n+1}+G_{n}\right)+\left(G_{n+1}+G_{n}\right) \\
&=\color{red}{3 G_{n+1}+2 G_{n}} \\
G_{n+5} &=G_{n+4}+G_{n+3} \\
&=\left(3 G_{n+1}+2 G_{n}\right)+\left(2 G_{n+1}+G_{n}\right) \\
&=\color{red}{5 G_{n+1}+3 G_{n}} \\
G_{n+6} &=G_{n+5}+G_{n+4} \\
&=\left(5 G_{n+1}+3 G_{n}\right)+\left(3 G_{n+1}+2 G_{n}\right) \\
&=\color{red}{8 G_{n+1}+5 G_{n}}
\end{aligned}$$となることから、フィボナッチ数列$\{F_n\}$と一般フィボナッチ数列$\{G_n\}$の間に$$\small G_{n+m}=F_{m} G_{n+1}+F_{m-1} G_{n} \quad \cdots (*)$$という関係式が見出されます。これを証明してみましょう。
証明
等式$$\small G_{n+m}=F_{m} G_{n+1}+F_{m-1} G_{n} \quad \cdots (*)$$が成り立つことを数学的帰納法により示す。
(ⅰ)$m=2,3$ のとき、$(*)$は成り立つ。
(ⅱ)$j$を$4$以上の整数として、$m \leqq j$ であるようなすべての$m$について$(*)$が成り立つと仮定する。このとき$$\small \begin{aligned}
G_{n+j}&=F_{j} G_{n+1}+F_{j-1} G_{n} \\
G_{n+(j-1)}&=F_{j-1} G_{n+1}+F_{j-2} G_{n}
\end{aligned}$$が成立し、これら2式を辺々加えると左辺は$$\small G_{n+j}+G_{n+(j-1)}=G_{n+(j+1)}$$となり、右辺は$$\small \begin{aligned}
& \quad \ \left(F_{j}+F_{j-1}\right) G_{n+1}+\left(F_{j-1}+F_{j-2}\right) G_{n} \\
&=F_{j+1} G_{n+1}+F_{j} G_{n}
\end{aligned}$$となるから$$\small G_{n+(j+1)}=F_{j+1} G_{n+1}+F_{j} G_{n}$$が成り立つ。よって$(*)$は $m=j+1$ のときも成り立つ。
以上(ⅰ)、(ⅱ)より、$(*)$は任意の正の整数$m$に対して成立する。
□
というわけで、等式$$\small G_{n+m}=F_{m} G_{n+1}+F_{m-1} G_{n}$$が成り立つので、$G_n$を$F_n$に入れ替えれば$$\small F_{n+m}=F_{m} F_{n+1}+F_{m-1} F_{n}$$を得ます。この関係式は「フィボナッチ数列の加法定理」と呼ばれるもので、この等式からフィボナッチ数列の様々な性質を導くことができます。
加法定理の応用
フィボナッチ数列の加法定理$$\small F_{n+m}=F_{m} F_{n+1}+F_{m-1} F_{n}$$において$m$に代入する正の整数は何でもOKです。
例えば $m=n$ とすれば$$\small F_{2n}=F_{n} F_{n+1}+F_{n-1} F_{n}$$ $$\small \therefore F_{2n}=F_{n}(F_{n-1}+F_{n})+F_{n-1} F_{n}$$ $$\small \therefore F_{2n}=F_{n}^2+2 F_{n-1} F_{n}$$といった関係式が得られます。これより、$F_{2n}$は常に$F_{n}$で割り切れることや、$n$が偶数のとき$F_{n}$は素数にならないことなどが分かります。
$m=n+1$ とすれば$$\small F_{2n+1}=F_{n+1}^2+F_{n}^2$$が得られます。これは前回の投稿で解説した2021年浜松医科大学前期数学第3問の(3)で導いた等式に他なりません。
先ほど$F_{2n}$が常に$F_{n}$で割り切れることを確認しましたが、加法定理を使えばより一般に「$n$が$m$で割り切れるなら、$F_n$は$F_m$で割り切れる」ことも証明できます。
$n$が$m$で割り切れるとき、ある整数$q$が存在して $n=mq$ と置けます。ここで$F_{mq}$が$F_m$で割り切れると仮定すると、加法定理より$$\begin{align} F_{m(q+1)} &=F_{mq+m} \\ &=\color{red}{F_{m}}\color{black}{F_{mq+1}+F_{m-1} }\color{red}{F_{mq}} \end{align}$$となるので、仮定も踏まえると赤字部分は$F_{m}$で割り切れることが言えます。
こうして「$n$が$m$で割り切れるなら、$F_n$は$F_m$で割り切れる」ことが帰納的に示されます。この系から、例えば$F_{2021}$が $F_{43}=433494437$ と $F_{47}=2971215073$ で割り切れることが直ちに従います。また、フィボナッチ数$F_n$が素数となるためには$n$もまた素数でなければならないことも分かりますし、任意の整数$k$に対して$k$の倍数となるようなフィボナッチ数$F_n$が(無数に)存在することも分かります。

“フィボナッチ数列の加法定理” への4件の返信