ヘッセ行列による多変数関数の極値判定

第2次偏導関数を成分とする「ヘッセ行列」の情報を使えば多変数関数の極値判定が可能です。今回は多変数関数の停留点に対する極値判定の方法について解説します。

3種類の停留点

勾配（1次微分）の値がゼロとなる点を「停留点」と呼びます。停留点には以下の3種類があります。

- - - 極大点
    - 極小点
    - 鞍点

いずれの点も勾配がゼロになっています。イメージとしては「平らになっている点」が停留点に相当します。例えば、2変数関数$$f(x,y)=\dfrac{1}{2}\sin x-\cos y$$を図示すると以下のようになります。

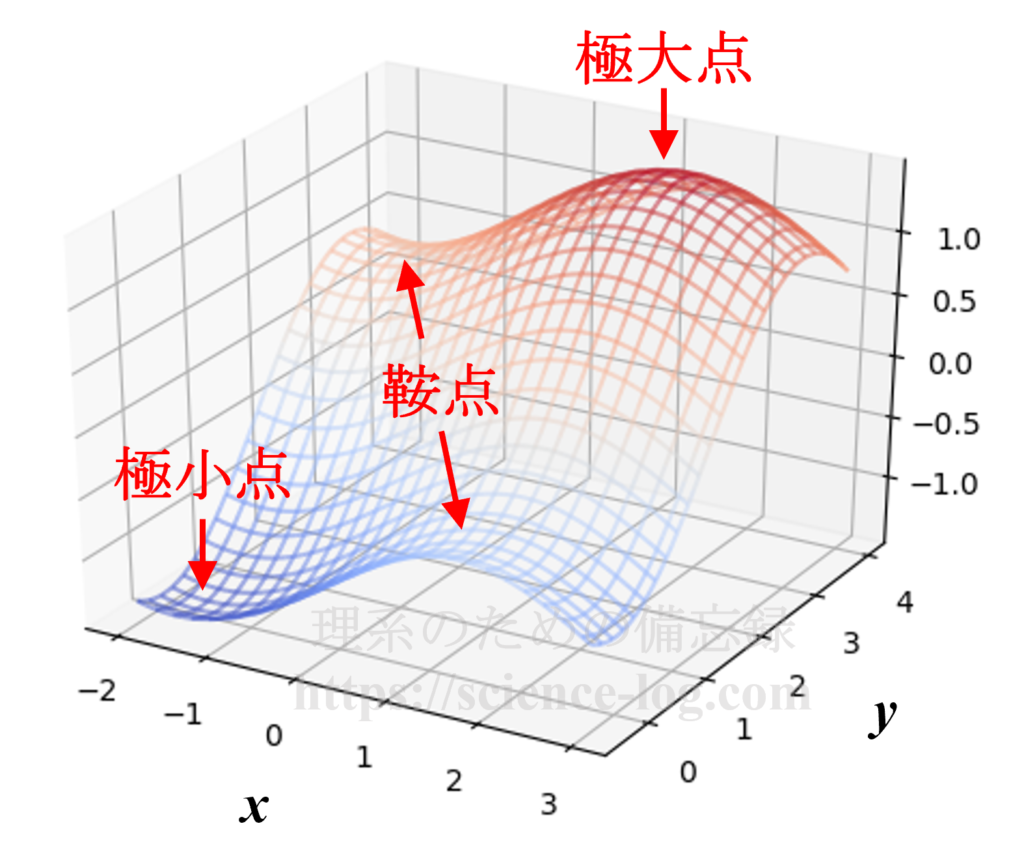
図示した範囲には極大点と極小点が１つずつ、鞍点が２つ存在しています。極大点と極小点はそのまま見た目から分かりますよね。鞍点というのは聞き慣れないかもしれませんが、その周辺が「馬の鞍くら」のような曲面になっていることから「鞍点」の名が付いています。

※「鞍」は英語で “Saddle” なので、英語で「鞍点」は “Saddle Point” と呼ばれています。

ヘッセ行列（ヘシアン）

$n$変数関数に対して2次微分を成分とする $n \times n$ の正方行列を「ヘッセ行列」または「ヘシアン」（Hessian）と呼びます。$$\mathbf{H} \equiv \left[\begin{array}{cccc}
\dfrac{\partial^{2} f}{\partial x_{1}^{2}} & \dfrac{\partial^{2} f}{\partial x_{1} \partial x_{2}} & \cdots & \dfrac{\partial^{2} f}{\partial x_{1} \partial x_{n}} \\
\dfrac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \dfrac{\partial^{2} f}{\partial x_{2}^{2}} & \cdots & \dfrac{\partial^{2} f}{\partial x_{2} \partial x_{n}} \\
\vdots & \vdots & \ddots & \vdots \\
\dfrac{\partial^{2} f}{\partial x_{n} \partial x_{1}} & \dfrac{\partial^{2} f}{\partial x_{n} \partial x_{2}} & \cdots & \dfrac{\partial^{2} f}{\partial x_{n}^{2}}
\end{array}\right]$$ヘッセ行列は2次微分であることを明示して$\nabla^2 f(\mathbf{x})$と表記されることもあります。

※「$\nabla$」は「ナブラ (nabla)」と呼ばれる「微分」を表す演算子です。また「ヘシアン」は「ヘッシアン」と呼ばれることもありますが、本質的に違いはありません。

※ここで「$\partial$」は偏微分の記号で「関数をある1種類の変数について微分していますよ」という意味の記号です。多変数関数に対してしか使いません。

⚠️偏微分の順序について

変数$x_{i}$で偏微分してから変数$x_{j}$で偏微分した第2次偏導関数と、変数$x_{j}$で偏微分してから変数$x_{i}$で偏微分した第2次偏導関数は一致します。第2次偏導関数はどちらの変数から先に偏微分して求めても変わらないので$$\dfrac{\partial^{2} f}{\partial x_{i} \partial x_{j}}=\dfrac{\partial^{2} f}{\partial x_{j} \partial x_{i}}$$が成り立ちます。つまりヘッセ行列は常に$n$次の対称行列となります。これより、ヘッセ行列の要素を計算する際は、下三角成分か上三角成分のいずれかを計算すれば十分です。

行列の正定値性と極値判定

以下のいずれかの条件を満たす行列 $A$ を「正定値行列」といいます。

1. 零ベクトルでない任意の列ベクトル$\mathbf{x}$に対して、二次形式 $\mathbf{x}^{\top}A\mathbf{x}$ が正
  　
2. $A$の固有値が全て正
  　
3. $A$のすべての首座小行列（左上側の $k \times k$ の正方行列）の行列式が全て正
  　　
4. $A$のすべての主小行列（第 $i$ 行と第 $i$ 列を除いて得られる小行列）の行列式が全て正
  　
5. ある正則行列$S$を用いて $A = SS^{\top}$ と書ける
  　
6. ある直交行列$Q$と対角要素が正の対角行列$D$を用いて $A = QDQ^{\top}$ と書ける

これらの条件は全て同値なので、どれか１つが成り立てば残りの５つも成り立ちます。行列 $-A$ が正定値のとき、元の行列 $A$ は負定値と定義されます。それ以外の場合、行列 $A$ は正定値でも負定値でもありません。

ヘッセ行列が正定値行列かどうかで極値判定ができるので、この行列の正定値性の判別は重要です。変数が少ない場合は条件３を使ってヘッセ行列の正定値性を調べるのが簡単です。

※$n$次正方行列は全部で$n$個の首座小行列を持ちます。例えば、$\left[\begin{array}{lll}1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9\end{array}\right]$の首座小行列は以下の通り。
1次：$\left[\begin{array}{l}1 \end{array}\right]$、2次：$\left[\begin{array}{ll}1 & 2 \\ 4 & 5 \end{array}\right]$、3次：$\left[\begin{array}{lll}1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9\end{array}\right]$

※主小行列とは「第 $i$ 行と第 $i$ 列を除いて得られる小行列」のことで、「対角成分を含む行と列を除いて得られる小行列」とも言い換えられます。詳しくは線形代数の教科書を参考にして下さい。$n$次正方行列の$k$次の主小行列は全部で${}_n \mathrm{C}_{k}$個存在します。例えば、$\left[\begin{array}{lll}1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9\end{array}\right]$の$2$次の主小行列は $\left[\begin{array}{ll}1 & 2 \\ 4 & 5 \end{array}\right]$、$\left[\begin{array}{ll}5 & 6 \\ 8 & 9 \end{array}\right]$、$\left[\begin{array}{ll}1 & 3 \\ 7 & 9 \end{array}\right]$ の$3$つです。

1変数関数の場合、以下のことが成り立ちます。

- 極値の必要条件： $x=a$ で極大 or 極小 $\Longrightarrow$ $f^{\prime}(a)=0$
- 極小の十分条件： $f^{\prime}(a)=0$ and $f^{\prime\prime}(a) > 0$ $\Longrightarrow$ $x=a$ で極小
- 極大の十分条件： $f^{\prime}(a)=0$ and $f^{\prime\prime}(a) < 0$ $\Longrightarrow$ $x=a$ で極大

これと同様のことが多変数関数でも成立します。

多変数関数の極値判定

- 極値の必要条件：
  $f(\mathbf{x})$が点$\mathbf{x}$で極値 $\Longrightarrow$ 点$\mathbf{x}$で偏導関数の値が全てゼロ
  　
- 点$\mathbf{x}$で偏導関数の値が全てゼロかつヘッセ行列が正定値
  $\Longrightarrow$ 点$\mathbf{x}$で極小
  　
- 点$\mathbf{x}$で偏導関数の値が全てゼロかつヘッセ行列が負定値
  $\Longrightarrow$ 点$\mathbf{x}$で極大

これを利用すれば微分可能な多変数関数$f(\mathbf{x})$の極値判定ができます。

極値判定してみる

実際に上記の公式を使って極値判定してみましょう。イメージしやすいように2変数関数の場合を考えます。2次のヘッセ行列は$$\mathbf{H}=\left[\begin{array}{cc}
\dfrac{{\partial}^2 f(\mathbf{x})}{\partial x^2} & \dfrac{{\partial}^2 f(\mathbf{x})}{\partial x \partial y} \\
\dfrac{{\partial}^2 f(\mathbf{x})}{\partial y \partial x} & \dfrac{{\partial}^2 f(\mathbf{x})}{\partial y^2}
\end{array} \right]$$と表されます。

例えば$$f(x,y)=x^2-3xy+y^2+y^3$$とすると、第1次偏導関数は$$\begin{cases} \dfrac{\partial f}{\partial x}=2x-3y \\ \dfrac{\partial f}{\partial y}=-3x+2y+3y^2 \end{cases}$$となり、第2次偏導関数は$$\begin{cases} \dfrac{\partial^2 f}{\partial x^2}=2 \\ \dfrac{\partial^2 f}{\partial x \partial y}=-3 \\ \dfrac{\partial^2 f}{\partial y^2}=6y+2 \end{cases}$$となります。よってヘッセ行列は$$\mathbf{H}=\left[\begin{array}{cc}
2 & -3 \\
-3 & 6y+2
\end{array} \right]$$で与えられ、行列式は$$\begin{align} \det(\mathbf{H})&=2(6y+2)-(-3)^2 \\ &=12y-5 \end{align}$$となります。

極値の必要条件を考えます。$\dfrac{\partial f}{\partial x}=\dfrac{\partial f}{\partial y}=0$ の連立方程式を解くと、偏導関数の値が全てゼロとなるのは$\left(0,\,0\right)$、$\left(\dfrac{5}{4},\,\dfrac{5}{6}\right)$の2点のみであることが分かるので、これらの点が極値の候補となります。この2点についてヘッセ行列で極値判定します。

まず点$\left(0,\,0\right)$について、ヘッセ行列の首座小行列を考えます。1次の首座小行列の行列式は$$2 \ (>0)$$で正ですが、2次の首座小行列の行列式は$$12 \cdot 0-5 =-5 \ (<0)$$と負になるので、ヘッセ行列は正定値でも負定値でもありません。したがって、点$\left(0,\,0\right)$は極値を与える点ではありません。（この場合は鞍点になっています）

次に点$\left(\dfrac{5}{4},\,\dfrac{5}{6}\right)$について、ヘッセ行列の首座小行列を考えます。1次の首座小行列の行列式は$$2 \ (>0)$$で正、2次の首座小行列の行列式も$$12 \cdot \dfrac{5}{6}-5 =5 \ (>0)$$と正になるので、ヘッセ行列は正定値です。したがって、点$\left(\dfrac{5}{4},\,\dfrac{5}{6}\right)$では偏導関数の値が全てゼロかつヘッセ行列が正定値なので、極小を与える点であることが分かります。

以上の結果が正しいことは、曲面を図示すると視覚的に理解できます。

このようにして、ヘッセ行列を用いた極値判定を行います。2変数関数の場合は「判別式」などを使って極値判定する方法もありますが、ヘッセ行列の正定値性を調べる方法の方が汎用性が高いと言えます。

鞍点と「虚の振動数」

ここからは数学を離れて、少し発展的な話に入ります。

多変数関数を一種のポテンシャル面と見なすとき、その偏微分はある次元における「力」のベクトルに対応します。つまり、ポテンシャル面上のある点における勾配は力という物理量に対応しているのです。

例えば以下のような「調和振動子」の場合、最低点から少しボールを動かすと、中心の位置に戻ろうとする力が働きます。これは物理学で「復元力」と呼ばれる力です。

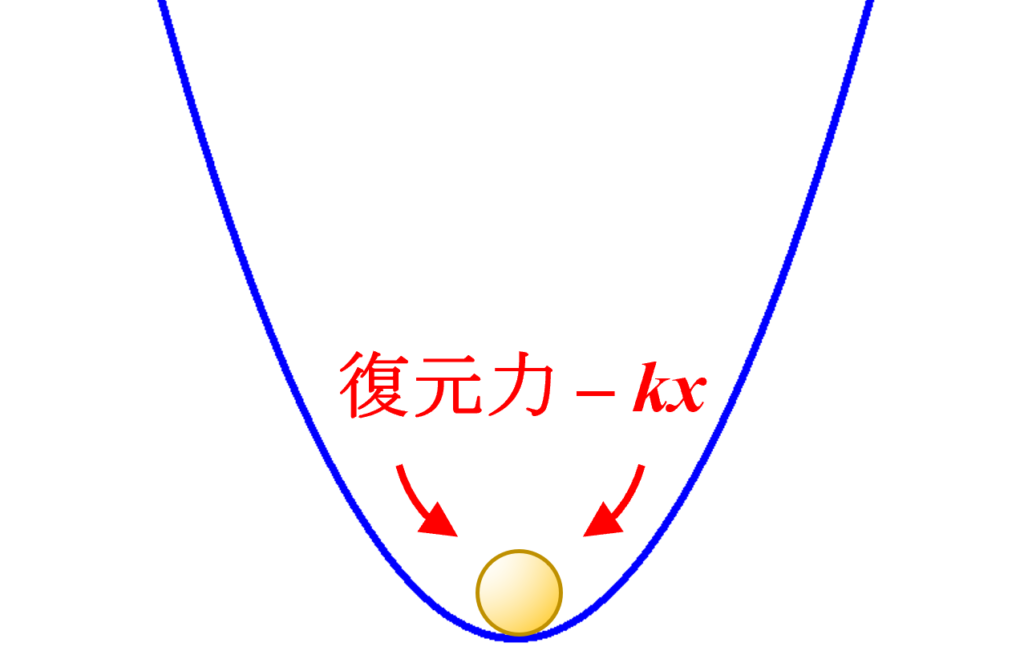
ここからは物理の内容になってしまうのですが、復元力$F$が変位$x$に比例して負方向に働くとすると、比例定数を$k\,(>0)$として$$F=-kx$$と書けます。ボールを質量$m$の質点とすれば運動方程式は$$m \ddot{x}=-kx$$となります。

※$\ddot{x}$は$x$の時間に関する2回微分、すなわち加速度を表します。

この両辺に速度$\dot{x}$を乗じて$x$に関して積分すると、$$\dfrac{1}{2}m \dot{x}^2=-\dfrac{1}{2}kx^2+C$$となります。ここで積分定数$C$を便宜上 $\dfrac{1}{2}kx_{0}^{2}$ と置くと、$$\dfrac{\mathrm{d} x}{\mathrm{d} t}=\sqrt{\dfrac{k}{m}\left(x_{0}^{2}-x^{2}\right)}$$となり、$\omega \equiv \sqrt{\dfrac{k}{m}}$ と置いて整理すると$$\omega \mathrm{~d} t=\dfrac{\mathrm{d} x}{\left(x_{0}^{2}-x^{2}\right)^{1 / 2}}$$となります。この両辺をそれぞれ積分して$$\omega t+\delta=\sin ^{-1} \dfrac{x}{x_{0}}$$ $$\therefore x=x_{0} \sin \left(\omega t+\delta\right)$$を得ます。

※式変形の途中で積分公式$$\displaystyle \int \dfrac{\mathrm{d} x}{\sqrt{a^2-x^{2}}}=\sin^{-1}\dfrac{x}{a}+C$$を用いました。これは大学教養レベルの解析学で学ぶ積分です。

結局、この一連の式変形から何が言いたいかと言うと「ボールは振動数$\omega$で振動運動をする」ということです。最初に変位（＝$x_{0} \sin \delta$）を与えられたボールは、振動数を $\omega \equiv \sqrt{\dfrac{k}{m}}$ として周期的な振動運動（単振動）をします。いま、$k$は正なので振動数$\omega$は実数ですが、$k$が負になる場合は振動数$\omega$は虚数となります。

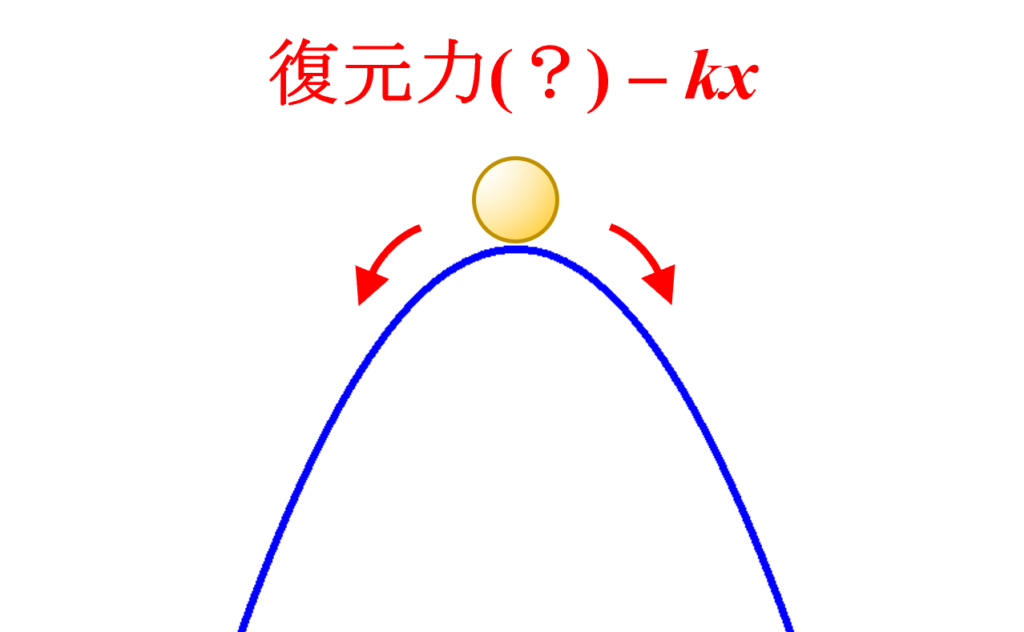
$k$が負になるケースというのは例えば、下図のようにポテンシャルの頂点にボールが設置してある場合に相当します。このボールに微小な変位を与えたら最後、転がりっぱなしで二度と初期位置に戻ってくることはありません。これは言うなれば、”負の” 復元力が働いているイメージです。このとき「振動数は虚である」とか「虚の振動数をもつ」という風に言います。

ここで、2変数関数の鞍点に立ち戻ってみましょう。上記の観点から、鞍点は「1方向にのみ虚の振動数を持っている停留点」と定義することができます。言い換えれば、鞍点ではある1方向以外の次元に対しては振動数が実数（固有値がただ1つを除いて正）となります。

これは以下の図を見れば何となく理解できると思います。確かに1方向にのみ虚振動（＝転がったボールが戻ってこない）していますよね。

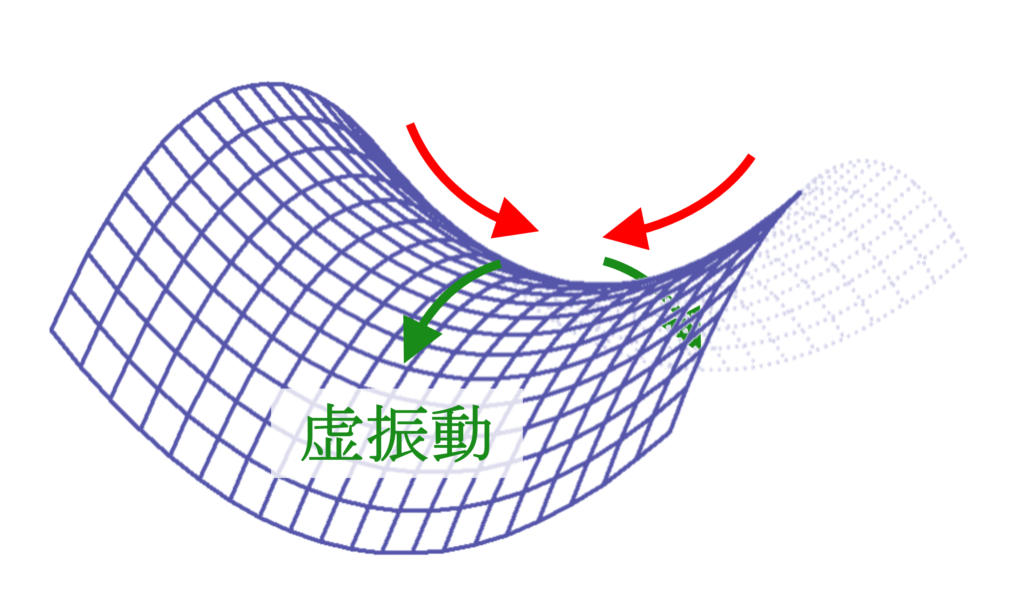
一般に、2次以上の関数上の鞍点ではヘッセ行列の固有値が一つだけ負になっています。これは鞍点がポテンシャル面上において1方向にのみ虚の振動数を持つ点であることに対応しています。

今は2変数関数を考えていたので非常に分かりやすかったのですが、より高次の多変数関数になると、ヘッセ行列の複数の固有値が負になることがあります。これは「高次の鞍点」と呼ばれるものに相当し、化学動力学などの理論化学の分野における研究対象になっています。化学反応における「遷移状態」は自由エネルギーポテンシャル面上の1次の鞍点として定義されており、ポテンシャル面上の鞍点をいかに効率よく収集するかが計算化学における課題の一つとなっています。

以上、余談でした。( ..)φ…ﾒﾓﾒﾓ