後期第1問目は一橋大学の整数問題です。問題はまたもTwitterから拾わせて頂きました。
《問題》
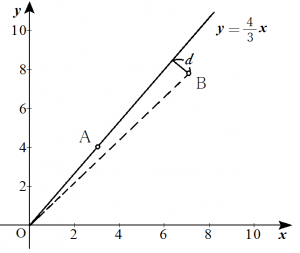
$m、n$を$1$以上$10$以下の整数とする。$3$点$\text{O}(0,0)$、$\text{A}(3,4)$、$\text{B}(m,n)$は同一直線上にないとする。
(1)$\triangle \text{OAB}$ の面積を最小にする$\text{B}(m,n)$を求めよ。
(2)$\angle \text{AOB}$ を最小にする$\text{B}(m,n)$を求めよ。
(一橋大学2017 後期第4問)
《考え方》
(1)は標準レベルの問題です。
$\triangle \text{OAB} = \dfrac{1}{2}|4m-3n|$ であり、$3$点は同一直線上にないから $4m-3n \ne 0$ です。故に $|4m-3n|=1$ のとき $\triangle \text{OAB}$ の面積は最小となります。$$4m-3n=\pm 1$$ $$\therefore \begin{cases} m=3k \pm 1 \\ n=4k \pm 1 \end{cases}$$ $1 \leqq m \leqq 10$、$1 \leqq n \leqq 10$ より、$$(m,n)=(1,1)、(2,3)、(4,5)、(5,7)、(7,9)$$を得ます。
(2)ですが、1変数化して微分を使うのかな?・・・と思いきや、(1)が利用できることに気付きました。しかし論理的なミスを誘発しやすい問題なので細心の注意を払う必要があります。
以下、$\angle \text{AOB}$ を考えるために取り敢えず $\sin \angle \text{AOB}$ を考えます(中には $\cos \angle \text{AOB}$ を考えた人もいると思いますが、これだと(1)の結果が活かせません(多分))。
$$\begin{align} \sin \angle \text{AOB} &= \dfrac{2 \cdot \triangle \text{OAB}}{\text{OA} \cdot \text{OB}} \\
&=\dfrac{|4m-3n|}{5 \sqrt{m^2+n^2}} \end{align}$$
となり、(1)によれば、ここから
$$\begin{align} \dfrac{|4m-3n|}{5 \sqrt{m^2+n^2}} & \geqq \dfrac{1}{5 \sqrt{m^2+n^2}} \\ & \geqq \dfrac{1}{5 \sqrt{7^2+9^2}} \\ &=\dfrac{1}{5 \sqrt{130}} \end{align}$$
となる・・・ということが言えそうですが、ここで解答を終了してしまうと(多分)$0$点です!なぜならこれが最小値である保証がどこにも無いからです。分子が最小値を取るときの $m、n$ の組が $\dfrac{|4m-3n|}{5 \sqrt{m^2+n^2}}$ を最小にするとは限りません。どういうことかというと、$|4m-3n| \geqq 1$ ではありますが、$|4m-3n|=1$ を満たす $m、n$ の組に制約がある(すべての $m、n$ の組が $|4m-3n|=1$ を満たす訳ではない)ため、$|4m-3n|=1$ のときではなく例えば $|4m-3n|=2$ のときに $\dfrac{|4m-3n|}{5 \sqrt{m^2+n^2}}$ が最小となるかもしれないからです。
ここで$|4m-3n|$について少し。
$3$と$4$は互いに素なので、基本的に$|4m-3n|$は任意の正の整数値を取ることができます。「基本的に」というのは、この問題設定では $1 \leqq m \leqq 10$、$1 \leqq n \leqq 10$ という制約があるために$|4m-3n|$が取り得る整数値がある程度制約される場合があることを踏まえて言っています。実際、$|4m-3n|$がある正の整数値$N$に等しくなるとき、この不定方程式を解いて$$\begin{cases} m=3k \pm N \\ n=4k \pm N \end{cases}$$を得ますから、このような $m、n$ の組を構成すれば$|4m-3n|$は任意の正の整数値を取ることができます。まずこのことは理解しておきましょう。
さて、先程は$\dfrac{1}{5 \sqrt{130}}$という値を得ましたが、これは一体何を表しているのでしょう?
・・・それを考える前に点$\text{B}(m,n)$と直線$\text{OA}$との距離$d$について考えておきます。点と直線の距離の公式から、$$d=\dfrac{|4m-3n|}{\sqrt{3^2+4^2}}=\dfrac{1}{\sqrt{5}}|4m-3n|$$と求められます。
$|4m-3n|$は任意の正の整数値を取る(さっきお話しした通りです)ので、$d$は $\dfrac{1}{5}、\dfrac{2}{5}、\dfrac{3}{5}、\cdots$ という値を取ることが分かりました。
いま、$\text{OB}=\sqrt{m^2+n^2}$ですから、$$\sin \angle \text{AOB}=\dfrac{d}{\text{OB}}=\dfrac{d}{\sqrt{m^2+n^2}}$$となります。つまり、先程求めたのは $d=\dfrac{1}{5}$ を満たすような点$\text{B}(m,n)$の集合の中で考えた時の$\sin \angle \text{AOB}$の最小値だった訳です。これがアヤシイというなら次に考えるべきなのは $d=\dfrac{2}{5}$ を満たす点$\text{B}(m,n)$の集合の中で考えた時の$\sin \angle \text{AOB}$の最小値ですよね。つまり、$$\dfrac{2}{5 \sqrt{m^2+n^2}}<\dfrac{1}{5 \sqrt{130}}$$を満たすような点$\text{B}(m,n)$が存在するのかしないのか、というのが最大の関心事ですから、これを解いてみます。すると、$$\sqrt{m^2+n^2}<2\sqrt{130}$$ $$\therefore m^2+n^2>520 \ \ \cdots \cdots (\ast)$$となりました。ここで、$1 \leqq m \leqq 10$、$1 \leqq n \leqq 10$という条件を思い出すと、$m^2+n^2$はどんなに頑張っても$200$までの値しか取れません。つまり$(\ast)$を満たすような点$\text{B}(m,n)$は存在しないことが分かりました。これは $|4m-3n| \geqq 2$ となるすべての場合について言えるので、$|4m-3n|=1$ となるときに最小値を取ることが分かりました。
よって $\sin \angle \text{AOB}$ の最小値は $|4m-3n|=1$ となるとき、つまり $d=\dfrac{1}{5}$ となるような点$\text{B}$のうち、$(m,n)=(7,9)$ のときに与えられるので、求める点$\text{B}$は$$(m,n)=(7,9)$$と決定することが出来ました。めでたしめでたし・・・。
(コメント)
さて、結局(2)答えは$\dfrac{1}{5 \sqrt{130}}$だったので、十分条件を全く確認しなくても正しい答えは得られてしまっていることになります。このこと、つまり点$\text{A}$がどこにあっても半直線$\text{OA}$との距離が最小となる点$\text{B}$を選べば $\angle \text{AOB}$ の最小値が得られることは一般的に成立するのでしょうか・・・?
見た目的に成り立ちそうな気もしますが、これは今後の研究課題ですね・・・。ともかく、(2)は難問とは言わないまでも、試験場で解くには(1)のヒント(?)が無いとなかなか難しい問題だったと思います。
因みに(1)で話題にしている $\triangle \text{OAB}$ の面積の最小値についてですが、格子点からなる三角形の面積の最小値は常に $\dfrac{1}{2}$ であることが知られています。まあこれは面積公式 $\dfrac{1}{2}|x_1 y_2 -x_2 y_1|$ を考えると自明と言えば自明なのですが・・・。