大阪医科大学の前期試験から三角形の辺に関連する整数問題をピックアップします。いわゆる「ナゴヤ三角形」とその仲間に関する問題です。
《問題》
$\triangle \mathrm{ABC}$は、3辺の長さ $\mathrm{BC}=a$、$\mathrm{CA}=b$、$\mathrm{AB}=c$ が整数で $\angle \mathrm{BAC}=\dfrac{\pi}{3}$ を満たすとする。
(1)$ab=21$ を満たすような$(a,b,c)$をすべて求めよ。
(2)$a+b+c=\dfrac{bc}{2}$ を満たすような$(a,b,c)$をすべて求めよ。
(大阪医科大学2019年 前期第1問)
《考え方》
角度が与えられているので、まずは余弦定理を用いて関係式を作りましょう。後は式変形で上手く絞り込みます。
解答例
(1)
$a,\,b,\,c$ は辺の長さなので正の整数であることに注意する。$\triangle \mathrm{ABC}$に対して余弦定理を適用すると$$\small \begin{align} & a^{2}=b^{2}+c^{2}-2 b c \cos \frac{\pi}{3} \\ \therefore & \,\, c^{2}-b c+b^{2}-a^{2}=0 \quad \cdots ① \end{align}$$を得る。①を$c$の二次方程式と見て判別式を考えると、$$\small \begin{align} D &=b^{2}-4\left(b^{2}-a^{2}\right)\\ &=4 a^{2}-3 b^{2} \geqq 0 \quad \cdots ② \end{align}$$となる。②を満たす$a$、$b$で $ab=21$ を満たすものは $(a,b)=(7,3),(21,1)$ のみである。
$(a,b)=(7,3)$ を①に代入して $c=8$ を得る。
$(a,b)=(21,1)$ を①に代入すると $c^2-c-440=0$ となり正の整数解をもたない。
以上より、$$\small (a,b,c)=\color{red}{(7,3,8)} \quad \cdots (\text{答})$$を得る。
※参考図: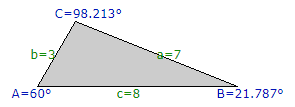
(2)
$\small a=\dfrac{b c}{2}-b-c$ の両辺を二乗すると$$\small a^{2}=\dfrac{b^{2} c^{2}}{4}-b^{2} c-b c^{2}+(a+b)^{2}$$となる。これを①に代入して整理すると$$\small b^{2} c^{2}-4 b^{2} c-4 b c^{2}+12 b c=0$$ $$\small \therefore (b-4)(c-4)=4 \quad (\because bc>0)$$と変形できる。これより$$\small (b,c)=(5,8),(6,6),(8,5)$$を得るので、$$\small \therefore (a,b,c)=\color{red}{(7,5,8),(6,6,6),(7,8,5)} \ \cdots (\text{答})$$と求められる。
※参考図:
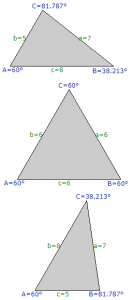
本問は整数問題としては基本レベルですが、題材は意外と奥深かったりします。1つの角が$60^{\circ}$で各辺の長さが整数であるような三角形の3辺は$$\small \begin{cases} a=m^2-mn+n^2 \\ b=2mn-n^{2} \\ c=m^2-n^2 \end{cases}$$で与えられることが知られています($m+n$ が$3$の倍数の場合については返信コメント欄を参照して下さい)。特に3辺が「7、5、8」の三角形を「ナゴヤ三角形」と俗称します。この名称は一松信先生の命名だそうです。遊び心がありますね(^▽^)
因みに、1つの角が$120^{\circ}$で各辺の長さが整数であるような三角形は「アイゼンシュタイン三角形」(Eisenstein triple) と呼ばれます。こちらの各辺は$$\small \begin{cases} a=m^{2}+m n+n^{2} \\ b=2 m n+n^{2} \\ c=m^{2}-n^{2} \end{cases}$$で与えられます。因みに、こちらは3辺が「7、5、3」の三角形が登場するので「和み三角形」と呼ばれることもあるとかないとか。

3数がすべて互いに素な場合の生成式について、1つの角が120度の場合はコメントの通りで大丈夫だと思いますが、60度の場合(m+nが3の倍数のとき)はm^2-mn+n^2、2mn-n^2、m^2-n^2を3で割らないとできない三角形があるようです。
廣津 孝さん
コメント頂き、ありがとうございます。
$$\begin{aligned} m^{2}-m n+n^{2} &=(m+n)^{2}-3 m n \\ 2 m n-n^{2} &=2 n(m+n)-3 n^{2} \\ m^{2}-n^{2} &=(m+n)(m-n) \end{aligned}$$であり、$m+n$ が$3$の倍数の場合は全ての辺の長さが$3$の倍数となるので、$3$で割らなければならないということですね。
最も簡単な例を挙げると、$m=2$、$n=1$ のとき各辺の長さが$3$の正三角形を与えますが、各辺の長さが$1$の正三角形はどのような$(m,n)$の組に対してもこれらの一般式からは得られません。
このような場合のために、$m+n$ が$3$の倍数の場合には既約な「ナゴヤ三角形」を得るために$3$で割る必要がある、ということのようです。
また「アイゼンシュタイン三角形」についても(まだよく確認していませんが)互いに素な整数組$(m,n)$に対して周期的に$3$が公約数として出現しているようです。
素因数の分布に関しては既によく調べられていそうな気がします。この辺りの話題は複素数平面とも絡んでくるので面白いですね。