こんにちは。管理人のpencilです。
2変数関数の最大最小に関する問題は教科書ではあまり扱われていませんが、入試の現場ではちらほら見かけるタイプの問題です。今回は表題の通り、高校数学の問題で偏微分を使って良いのかについて考えてみます。2変数関数の最大最小を求める手法である「予選決勝法」についても扱います。
2変数関数の問題
2変数関数を扱う問題を処理する方法は幾つか知られていますが、例えば次のような問題はその中でも最も単純な部類に該当するでしょう。
例題1
実数 $x$、$y$ の関数$$f(x,y)=x^2+2x+y^2+4y+8$$の最小値を求めよ。
このような問題であれば式変形(平方完成)だけで容易に解けますが、世の中そう甘くありません。(この関数は$(x, y) = (-1, -2)$ のとき最小値$3$をとる)
次の問題はどうでしょうか?
例題2
すべての正の実数 $x$、$y$ に対し$$\sqrt{x}+\sqrt{y}\leqq k\sqrt{2x+y}$$が成り立つような実数 $k$ の最小値を求めよ。
あまり馴染みの無いタイプの問題ですが、斉次式(両辺の次数が等しい等式)なので $t=\dfrac{\sqrt{x}}{\sqrt{y}}$ などと置けば1変数で処理できます。因みにこれは1995年の東大文理共通第1問(前期試験)の問題です。
では次の問題にはどう対処すべきでしょうか?
例題3
実数 $x$、$y$ の関数$$f(x,y)=\dfrac{8x+4y+2}{x^2+6y^2+8}$$の最大値および最小値を与える組($x$、$y$)を求めよ。
先日の創作整数問題#56と同じ関数ですが、こちらは変数が実数になっています。この関数$f(x,y)$を $-5<x,y<5$ の範囲で立体的に図示すると以下のようになります。
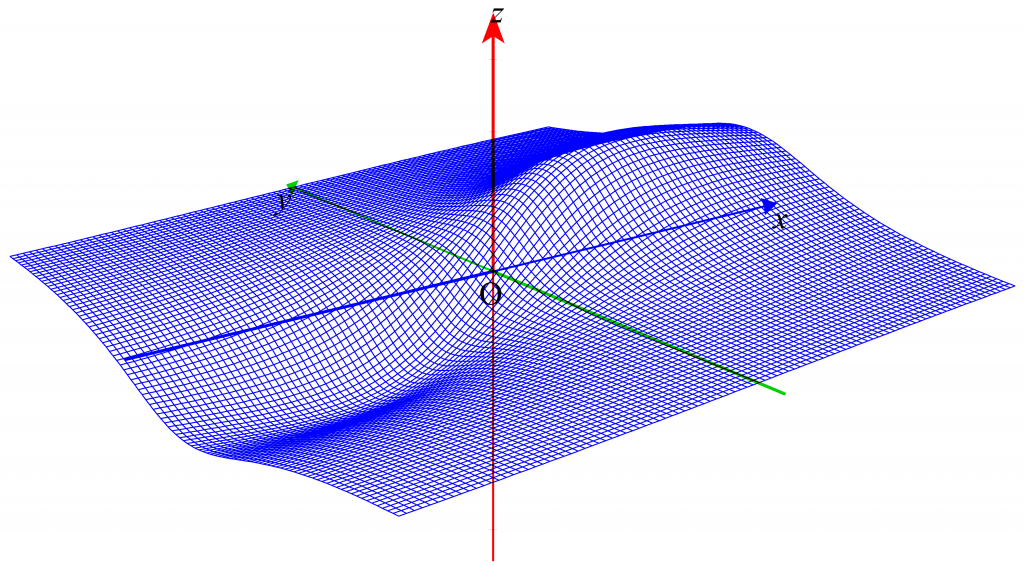
山と盆地が1つずつあるのが、この図から見て取れます。実際に関数$f(x,y)$の最大値と最小値は1つずつあるのですが、その計算は一筋縄ではいきません。
「予選決勝法」とは?(少し偏微分的な考え方)
世の中には「予選決勝法」と呼ばれる2変数関数の最大最小問題の解法が知られています。
「予選決勝法」
① ある1種類の文字のみに注目して他の文字を定数とみて固定し、1変数関数として最大値(or最小値)を考える。
② 固定していた文字を変数と見なし、①で求めた最大値(or最小値)のさらに最大値(or最小値)を求める。
手順①、手順②がそれぞれ予選と決勝に似ているため、この名が付けられています。この解法は「1文字固定法」と呼ばれることもあります。複雑そうですが、やっていることは単純です。
簡単な例に適用してみます。
例題4
実数 $x$、$y$ の関数$$f(x,y)=e^{1-2x^2-(y+1)^2}$$の最大値を与える組$(x,y)$を求めよ。
$z=e^{1-2x^2-(y+1)^2}$ は$(0,\,-1)$を頂点とするガウシアン(ガウス型関数)なので最大値はすぐに求められますが、ここでは「予選決勝法」で解いてみます。
まず$y$を固定して(定数と見なして)$z=e^{1-2x^2-(y+1)^2}$ を$x$で微分すると、$$\dfrac{dz}{dx}=-4 x e^{1-2x^2-(y+1)^2}$$を得ます。$\dfrac{dz}{dx}$は $x=0$ の前後で符号が入れ替わり、$x<0$ では正、$x>0$ では負なので、関数 $z=f(x,y)$ は $x=0$ で極大かつ最大となります。
次に関数 $z=f(0,y)$ を考えます。$$f(0,y)=e^{1-(y+1)^2}$$より、これを$y$で微分すると$$\dfrac{dz}{dy}=-2(y+1) e^{1-(y+1)^2}$$を得ます。このとき$\dfrac{dz}{dy}$は $y=-1$ の前後で符号が入れ替わり、$y<-1$ では正、$y>-1$ では負なので、関数 $z=f(0,y)$ は $y=-1$ で極大かつ最大となります。
以上より、求める組$(x,y)$は$$(x,y)=\color{red}{(0,-1)}$$となります。
● ● ●
まず$y$を固定し、最大値①($y$で表される式)を求めます。この最大値①を決定する際に場合分けが必要になることもあります。この作業は関数 $z=f(x,y)$ を以下のようにスキャンする様子に似ています。

その結果、関数 $z=f(x,y)$ の最大値を与える点は $x=0$ 上に存在することが分かるので、今度は関数 $z=f(x,y)$ に $x=0$ を代入して得られる以下の曲線上で、さらにその最大値を求めます。
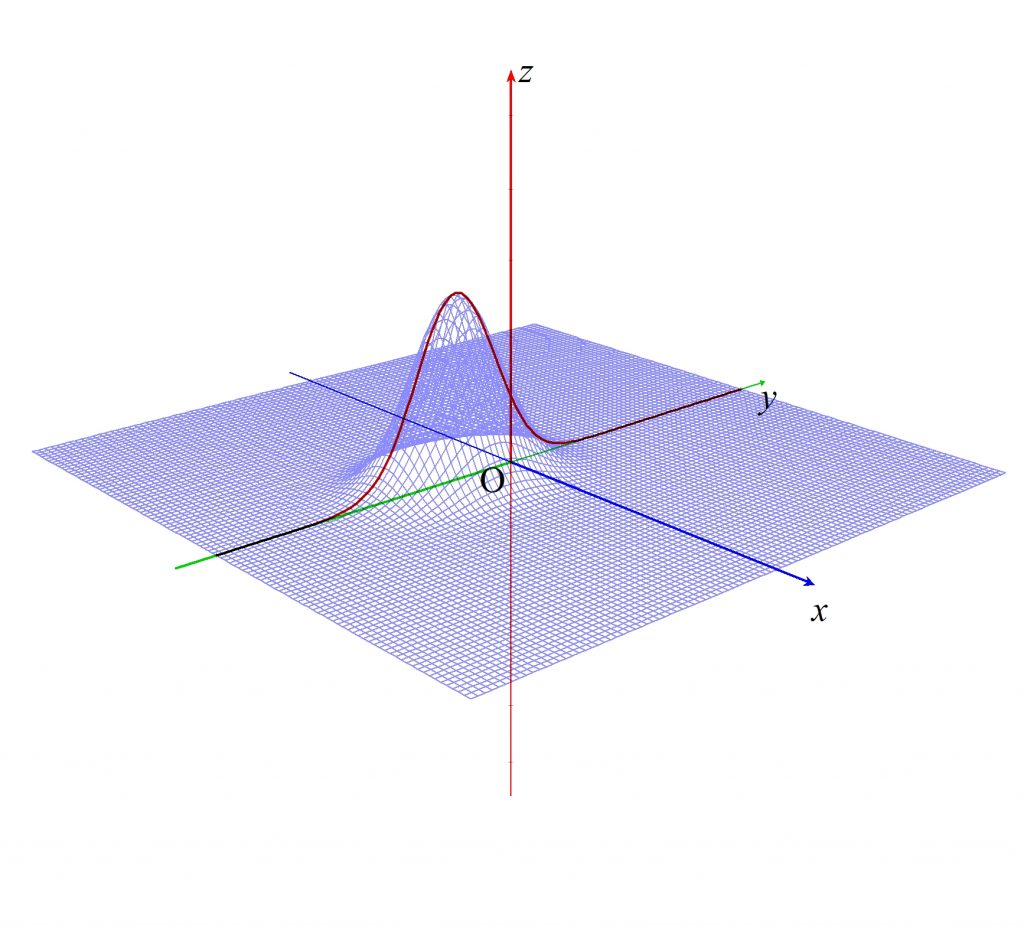
こうして得られる点が、山の頂上に相当する点 $(x,y)=(0,-1)$ というわけです。
● ● ●
予選決勝法の手続きは、
①一方の変数を定数と見て最大値$M$を求める
②変数の固定を解除し、さらに$M$の最大値を求める
(以下、変数の数だけ繰り返す)
という流れになっていて、慣れれば結構簡単に使える手法です。今回の例題は単純すぎて予選決勝法を使うメリットをあまり感じませんが、2変数がより複雑に入り組んでいるときに威力を発揮します。
偏微分を使うと?
一方、例題4を偏微分を用いて解くと以下のようになります。
最大値を与える点においては、$x$方向、$y$方向ともに傾きがゼロ、つまり$$\dfrac{\partial z}{\partial x}=\dfrac{\partial z}{\partial y}=0$$を満たすことが必要です。ここで、$\dfrac{\partial z}{\partial x}$は $z=e^{1-2x^2-(y+1)^2}$ を$x$で偏微分したもの、つまり、$y$を定数扱いして変数$x$で微分したものです。同様に$\dfrac{\partial z}{\partial y}$は$z$を$y$で偏微分したものです。
これらを計算すると、$$\begin{cases} \dfrac{\partial z}{\partial x}=-4 x e^{1-2x^2-(y+1)^2} \\ \dfrac{\partial z}{\partial x}=-2 (y + 1) e^{1-2x^2-(y+1)^2} \end{cases}$$となるので、$$\begin{cases} -4 x e^{1-2x^2-(y+1)^2}=0 \\ -2 (y + 1) e^{1-2x^2-(y+1)^2}=0 \end{cases}$$が必要です。これを解くと、$$\begin{cases} x=0 \\ y=-1 \end{cases}$$を得るので、$(x,y)=(0,-1)$に停留点をもつことが分かります。最大値を与える点の候補はこれしかないので、求める組$(x,y)$は$$(x,y)=(0,-1)$$となります。
※停留点とは、簡単に説明すると「関数の(偏)微分がどの変数に関してもゼロになる点」を指します。頭の中に地形を思い浮かべてみて下さい。山頂や盆地の一番低い所では傾斜がどの方向に対してもゼロになっていますよね?そういう点のことを停留点と呼びます(もちろん3次元以上でも停留点は存在しますし、「鞍点」と呼ばれる停留点も存在します)。
ここで$$\dfrac{\partial^2 z}{\partial x^2} = 4 (4 x^2 – 1) e^{1-2x^2-(y+1)^2}$$ $$\dfrac{\partial^2 z}{\partial y^2} = (4 y^2 + 8 y + 2) e^{1-2x^2-(y+1)^2}$$であり、これらに$(x,y)=(0,-1)$を代入するといずれも負なので、関数 $z=f(x,y)$ は$(x,y)=(0,-1)$で$x$方向、$y$方向のいずれに対しても上に凸であることが分かります。このことから関数 $z=f(x,y)$ が$(x,y)=(0,-1)$で最大となることが言えそうですが、本当はこれだけでは不十分で、2変数関数の判別式を用いてちゃんと最大値をとるのかを確かめる必要があります。
2変数関数$z$の判別式は$$D=\dfrac{\partial^2 z}{\partial x^2} \dfrac{\partial^2 z}{\partial y^2}-\left(\dfrac{\partial^2 z}{\partial xy}\right)^2$$で定義され、$D$が正のときに関数$z$は極値をもち、$\dfrac{\partial^2 z}{\partial x^2}>0$ なら極小値、$\dfrac{\partial^2 z}{\partial x^2}<0$ なら極大値をとります(この事実の証明はやや難しく、大学の教養課程で学ぶことになると思います。また、$D$の符号を逆に定義している教科書もあります)。
いま、$z=e^{1-2x^2-(y+1)^2}$ について判別式を計算すると、$$D=-8 e^{-4 x^2 – 2 y^2 – 4 y} (4 x^2 + 2 y^2 + 4 y + 1)$$となり、これに$(x,y)=(0,-1)$を代入すると$$D=8e^2>0$$であり、また、$\dfrac{\partial^2 z}{\partial x^2}<0$ なので関数$z$は極大値をとります。さらに、$|x| \to \infty$、$|y| \to \infty$ などの場合に関数が発散しないことを証明することで、結果的にこの極大値が最大値となることが示されます。
● ● ●
このように、偏微分を使っても解けないことはありませんが、極値の存在や種類の判別などの論証に気を遣う必要があります。偏微分を使った解答は予選決勝法に比べて示すべきことがかえって多くなってしまい、敢えて答案にするメリットが無いような気がします。そもそも大学入試では偏微分を使わないと解けないような問題は出題されませんし、大学によって採点基準がかなり違い、運用方法が間違っていると大幅に減点されたり、採点基準を他の受験生よりも厳しくされてしまう可能性があります。大学範囲の知識が適当に使われている答案からは入試問題を雑に扱っている印象を受け、採点官の心証を損なう危険性もあります。「生兵法は大怪我のもと」ということで、偏微分を大学入試で使用することは推奨できません。
偏微分を使わないと解けない?
結論から言うと、そんな問題は出ません。・・・が、問題の作り方を間違えると1文字固定法では歯が立たない問題が出来上がってしまいます。例えば先ほどのこの問題です。
例題3
実数 $x$、$y$ の関数$$f(x,y)=\dfrac{8x+4y+2}{x^2+6y^2+8}$$の最大値および最小値を与える組($x$、$y$)を求めよ。
この関数$f(x,y)$は、
$\small (x,y)=\left(\dfrac{-6+2 \sqrt{1209}}{25},\,\dfrac{-3+\sqrt{1209}}{150}\right)$のとき
最大値 $\dfrac{3+\sqrt{1209}}{24}$
$\small (x,y)=\left(\dfrac{-6-2 \sqrt{1209}}{25},\,\dfrac{-3-\sqrt{1209}}{150}\right)$のとき
最小値 $\dfrac{3-\sqrt{1209}}{24}$
をとります。ただし、これらの値は高校数学の範囲で(例えば「予選決勝法」などで)マトモに計算して得られる値ではない気がします。
(2019/11/23追記:当サイトがいつもお世話になっているHN たけちゃん さんから例題3の解法についてコメントを頂きました)
関数$f(x,y)$を$x$について偏微分すると$$\begin{aligned}&\ \ \ \dfrac{\partial}{\partial x}\left(\dfrac{8 x + 4 y + 2}{x^2 + 6 y^2 + 8}\right) \\ & = -\dfrac{4 (2 x^2 + 2 x y + x – 4 (3 y^2 + 4))}{(x^2 + 6 y^2 + 8)^2} \end{aligned}$$となり、$y$について偏微分すると$$\begin{aligned}&\ \ \ \dfrac{\partial}{\partial y}\left(\dfrac{8 x + 4 y + 2}{x^2 + 6 y^2 + 8}\right) \\ & = \dfrac{4 (x^2 – 24 x y – 6 y^2 – 6 y + 8)}{(x^2 + 6 y^2 + 8)^2} \end{aligned}$$となります。
したがって$$\begin{cases} 2 x^2 + 2 x y + x – 4 (3 y^2 + 4)=0 \\ x^2 – 24 x y – 6 y^2 – 6 y + 8=0 \end{cases}$$が停留点となるための必要条件で、この連立方程式を(頑張って)解くと$$x=\dfrac{-6+2 \sqrt{1209}}{25},\,y=\dfrac{-3+\sqrt{1209}}{150}$$および$$x=\dfrac{-6-2 \sqrt{1209}}{25},\,y=\dfrac{-3-\sqrt{1209}}{150}$$ という2つの実数解を得ます。
※なお、虚数解は$$x=\dfrac{-12+\sqrt{806}\,i}{50},\,y=\dfrac{-1-2\sqrt{806}\,i}{50}$$および$$x=\dfrac{-12-\sqrt{806}\,i}{50},\,y=\dfrac{-1+2\sqrt{806}\,i}{50}$$となります。
この実数解と先ほど使った2変数関数の判別式により、最大・最小を決定することができます(関数が発散しないことの確認も忘れずに)。
● ● ●
この例題3は偏微分を使わないと解くのが大変ですが、そもそも偏微分を使わないと解けないような問題が入試に出題されることはありません。確かに偏微分を使えば簡単に答えが推測できる問題も世の中には存在しますが、偏微分を用いた解答をそのまま答案として提出してしまうのはかなり微妙です。大学入試の範囲では偏微分の利用を確かめ算程度に留めておくのが良いでしょう。
昔、何かの模試(どこかの東大模試だったかな…?)で偏微分を使い、大問一つで満点を取っていた同級生がいましたが、アルバイトが担当している模試の採点と実際の入試の採点の質には天地ほどの差があります。模試で大学範囲の知識を使って良い成績が取れていたからと言って、入試でも同じように評価されるとは限りません。むしろ「あ、この子は大学レベルの数学を理解しているんだな」と採点官の教授が判断して、かえって数学的な厳密さが求められてしまうなんてことにもなりかねません。どうしても使いたいというのであれば止めませんが、使い所には細心の注意が必要です。
なお、予選決勝法そのものは偏微分ではないので、実際の試験問題で使える状況であれば使ってしまって問題無いでしょう。
(2021/09/29追記:記事中のスタイルを一部変更)

例題3を高校数学の範囲で解いてみます.
予選決勝法でもできないことはないでしょうが,面倒な気がするのでスルーです.
f(x,y)=kを満たす実数x,yが存在するような実数kの最大値,最小値を考える.
なお,8x+4y+2は正の値も負の値もとり,x^2+6y^2+8>0であるから,
f(x,y)は正にも負にもなり得て,最大値,最小値を考える際はk≠0としてよい.
f(x,y)=k(≠0)は,(x^2+6y^2+8)-(8x+4y+2)/k=0,すなわち
(x-4/k)^2+6(y-1/(3k))^2+8-2/k-50/(3k^2)=0と同値であり,
これを満たす実数x,yが存在する条件は,
(24k^2-6k-14)/(3k^2)≦0.
これを解いて,k≠0かつ(3-√1209)/24≦k≦(3+√1209)/24となるから,
求める最大値は(3+√1209)/24,最小値は(3-√1209)/24.
また,最大値,最小値を与えるx,yは,x=4/k,y=1/(3k)であり,
最大のとき,
x=96/(3+√1209)=96(√1209-3)/1200=2(√1209-3)/25,
y=x/12=(√1209-3)/150.
最小のとき,
x=96/(3-√1209)=-96(√1209+3)/1200=-2(√1209+3)/25,
y=x/12=-(√1209+3)/150.
たけちゃん さん
コメントありがとうございます。
確かに $f(x,y)=k$ と置く方法だとわざわざ偏微分を持ち出さなくても高校数学の範囲で容易に解決できますね!
別解のご提供に感謝致します!