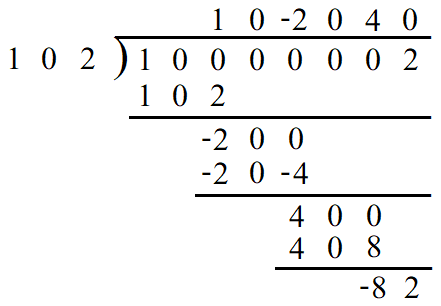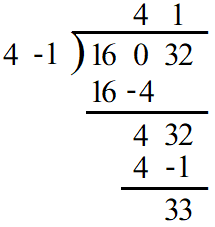一時期落ち着いていたかに思われた猛暑ですが、また猛威を振るい始めています。エアコンの温度設定は控えめにした方が良いですが、付けないと命にかかわる場合があります・・・。
創作整数問題#44
《問題#44》
$\displaystyle \sum^{n}_{k=1}k^p=S_p(n)$ と表すとき、$\dfrac{S_5(n)}{S_3(n)}$が平方数となるような正の整数$n$は無数に存在することを示せ。ここで平方数とは、ある整数の二乗になる整数をいうものとする。
(創作問題)
一見しただけでは分かりませんが、実はペル方程式に関する問題です。ヒントとして5乗和の式を載せておきましたが、力試しも兼ねて自力で求めてみましょう。
» ヒントはこちら
$\color{red}{\displaystyle \sum^{n}_{k=1}k^5=\dfrac{1}{12}n^2(n+1)^2(2n^2+2n-1)}$ です。
» 閉じる
創作整数問題#43(解き方)
| $A=2019^{2019}+1$ とするとき、$A^7+2$ と $A^2+2$ の最大公約数を求めよ。 |
|---|
多項式に対してユークリッドの互除法を用います。まず $A^7+2$ を $A^2+2$ で割りましょう。計算の流儀は色々あるでしょうが、多項式同士の除法では、私は以下のように計算しています。
本問の場合は項が少ないのであまり有難みが感じられないかもしれませんが、係数だけを書き出す方法だと書く量が少なくて済み、時間の節約になるのでオススメです。
さて、これより$$A^7+2=(A^5-2A^3+4A)(A^2+2)-8A+2$$となるので、$A^7+2$ と $A^2+2$ の最大公約数は $A^2+2$ と $-8A+2$ の最大公約数に等しいことが言えます。いま、$A=2019^{2019}+1$ ですから、$A$は偶数です。したがって $A^2+2$ は偶数なので、求める最大公約数を$g$とすると、$g$は偶数となることが分かります。$-8A+2$ を$2$で割ったものは $-4A+1$ であり、これは奇数なので $-4A+1$ は$\dfrac{g}{2}$の倍数となりますから、$A^2+2$ と $-4A+1$ の最大公約数は$\dfrac{g}{2}$です。$-1$を掛けても素因数は変わらないので、結局は $A^2+2$ と $4A-1$ の最大公約数を求めればよいことになります。
そうと分かれば $A^2+2$ を $4A-1$ で割ってしまえばよいのですが、ここで商が分数にならないように少し細工をします。$4A-1$ は$16$と互いに素なので、$16A^2+32$ と $4A-1$ の最大公約数は$\dfrac{g}{2}$のままです。そこで $16A^2+32$ を $4A-1$ で割ると、$$16A^2+32=(4A+1)(4A-1)+33$$となります。(※筆算は以下のようになります)
これより、$\dfrac{g}{2}$は $4A-1$ と $33$ の最大公約数に一致することが分かります。$33=3 \cdot 11$ なので、$4A-1$ が$3$の倍数かどうか、また、$11$の倍数かどうかについて調べましょう。
$$4A-1 \equiv A-1 \pmod{3}$$であり、$$A=2019^{2019}+1 \equiv 0+1 \pmod{3}$$より、$$4A-1 \equiv 0 \pmod{3}$$となります。よって $4A-1$ は$3$の倍数です。
また、$2019 \equiv 6 \pmod{11}$、$2019^2 \equiv 3 \pmod{11}$、$2019^4 \equiv 9 \pmod{11}$、$2019^5 \equiv 10 \equiv -1 \pmod{11}$ より、$$2019^{10} \equiv 1 \pmod{11}$$を得るので、$$\begin{align} 2019^{2019} &=2019^{2010} \cdot 2019^{5} \cdot 2019^{4} \\ &\equiv 1^{201} \cdot (-1) \cdot 9 \pmod{11} \\ &=2 \end{align}$$となり、$A \equiv 3 \pmod{11}$ と分かります。よって$$\begin{align} 4A-1 &\equiv 4 \cdot 3-1 \pmod{11} \\ &=11 \\ &\equiv 0 \pmod{11} \end{align}$$となるので $4A-1$ は$11$の倍数です。
以上より、$4A-1$ と $33$ の最大公約数は$33$であり、これが$\dfrac{g}{2}$に相当するので、求める最大公約数は$$\color{red}{66}$$となります。
(コメント)
$A$の値が巨大であるという以外は典型的な問題だったかと思います。典型的とは言っても整式の公約数を題材とした整数問題はあまり見かけない気がします。ここ最近では2017年の学習院大(理系)などで出題されています。整式の除算を題材とした整数問題は2015年の京都大(理系)などに出題があります。
本問に関してですが、実は $A^n+2$ と $A^2+2$ の最大公約数は正の整数$k$を用いて $n=5k+2$ となるときに限り$66$となり、それ以外の場合は$6$となります。($n=2$ のときは除きます。念のため。)これは$\bmod{11}$ を考えれば容易に分かりますね!