もう4月ですね。コロナウイルス対策も大事ですが、この時期は花粉対策のために必死にマスクで防護している方も多いのではないでしょうか。花粉症のために鼻詰まりしている人は無意識のうちに口呼吸の頻度が増えるため、ウイルスを吸引するリスクが高まります。また、症状が重くなるとくしゃみの回数が増えるため、周囲の飛沫感染のリスクも高くなってしまいます。
花粉対策はウイルス対策も同時に兼ねています。花粉症に悩まされている人は想像以上に周囲に気を遣っているはずです。決して邪険にせず、優しく労わってあげて下さい…。
創作整数問題#78
《問題#78》
等式$$\dfrac{5}{78}=\dfrac{1}{a}+\dfrac{1}{b}$$を満たす正の整数組$(a,b)$をすべて求めよ。
(創作問題)
いわゆるエジプト分数の話題です。不等関係を設定して解の範囲を絞り込むところまでは誰でもできると思いますが、それだけでは解を見つけるには不十分です。昨年の「数学夏祭り」第1問のように分母が素数であれば比較的容易なのですが、ここでは$a$と$b$の最大公約数を置く方針をとるのが良いでしょう。
» 答えはこちら
求める正の整数組$(a,b)$は$$\small \color{red}{(16, 624),\,(18, 117),\,(26, 39),\,(39, 26),\,(117, 18),\,(624, 16) }$$です。
» 閉じる
創作整数問題#77(解き方)
| 以下の2つの条件を同時に満たすような座標平面上の放物線$C$が存在することを示せ。 条件$(1)$:異なる$3$つの格子点で、これらを頂点とする三角形が二等辺三角形にならず、かつ、その面積が$77$となるようなものが$C$上に存在する。 条件$(2)$:整数 $a,b,c$ を用いて $y=ax^2+bx+c$ という形の方程式で表せる。 ここで、座標平面上における格子点とは、$x$座標と$y$座標がともに整数であるような座標平面上の点である。 |
|---|
当たり前のことですが、放物線は平行移動しても放物線です。そこで三角形の頂点の一つが原点に一致するように座標を設定すれば、三角形の面積計算がとてもラクになります。このようにすれば放物線$C$は原点を通るため、定数項$c$を考えなくても済みます。
解答例
条件$(1)$を満たすような三角形の頂点はすべて格子点であるから、そのうちのある1点が原点に一致するように平行移動しても三角形の頂点はすべて格子点のままである。また、条件を満たす放物線$C$について、$x$軸に関して対称な放物線もまた条件を満たす。これより、原点を通る下に凸な放物線$$y=ax^2+bx$$の場合を考えれば十分である。ここで$a$は正の整数、$b$は任意の整数である。
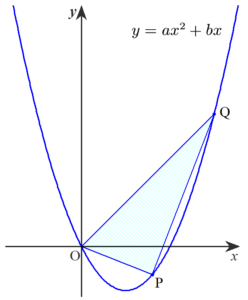
原点以外の頂点を$\mathrm{P}$、$\mathrm{Q}$として点$\mathrm{P}$、$\mathrm{Q}$の$x$座標をそれぞれ$p$、$q$と置く。ここで三角形の頂点のうち$x$座標が最も小さい点を原点とすれば、$p$、$q$は $0<p<q$ を満たす整数としてよい。$\triangle \mathrm{OPQ}$の面積は$$\small \begin{aligned}
\triangle \mathrm{OPQ} &=\frac{1}{2}\left|x_{\mathrm{P}}y_{\mathrm{Q}}-x_{\mathrm{Q}} y_{\mathrm{P}}\right| \\
&=\frac{1}{2}\left|p\left(a q^{2}+b q\right)-q\left(a p^{2}+b p\right)\right| \\
&=\frac{1}{2}|pq\{(a q+b)-(a p+b)\}| \\
&=\frac{1}{2}|apq(q-p)| \\
&=\frac{1}{2} a p q(q-p) \quad (\because 0<p<q)
\end{aligned}$$で与えられる。これより、本問は等式$$\dfrac{1}{2} a p q(q-p)=77$$ を満たす整数$p$、$q$($0<p<q$)が存在するような正の整数$a$を求める問題に帰着する。
ここで、$p$と$q$の偶数と奇数の別にかかわらず$pq(q-p)$は偶数となることに注意する。$$apq(q-p)=154 \quad \cdots (*)$$の右辺は素因数$2$を$1$個しかもたないから、$a$が偶数だとすると$(*)$の左辺は$4$の倍数となり不合理。よって少なくとも$a$は奇数であり、かつ$77$の約数に限られるから、$$a=1,\,7,\,11,\,77$$の$4$つに絞られる。
$a=1$ のとき、$(*)$は$$pq(q-p)=154$$となる。ここで$154$を3つの正の整数の積で表すと$$\begin{align}154 &= 1 \times 2 \times 77 \\ &= 1 \times 7 \times 22 \\ &= 1 \times 11 \times 14 \\ &= 2 \times 7 \times 11 \end{align}$$の4通りのみで、$(*)$の左辺がこのような形の積となる$p$、$q$の組は存在しない。
$a=7$ のとき、$(*)$は$$pq(q-p)=22$$となる。ここで$22$を3つの正の整数の積で表すと$$\begin{align}22 &= 1 \times 2 \times 11 \end{align}$$の1通りのみで、$(*)$の左辺がこのような形の積となる$p$、$q$の組は存在しない。
$a=11$ のとき、$(*)$は$$pq(q-p)=14$$となる。ここで$14$を3つの正の整数の積で表すと$$\begin{align}14 &= 1 \times 2 \times 7 \end{align}$$の1通りのみで、$(*)$の左辺がこのような形の積となる$p$、$q$の組は存在しない。
$a=77$ のとき、$(*)$は$$pq(q-p)=2$$となる。ここで$2$を3つの正の整数の積で表すと$$\begin{align}2 &= 1 \times 1 \times 2 \end{align}$$の1通りのみであり、$(p,q)=(1,2)$のとき、$(*)$の左辺はこのような形の積になる。
以上より、例えば放物線$C$の方程式を $y=77x^2$ とすれば、$C$上に存在する3点 $(0,\,0)$、$(1,\,77)$、$(2,\,308)$ を頂点とする三角形は二等辺三角形にならず、かつ、その面積は$77$となる。よって、条件$(1)$と$(2)$を同時に満たすような座標平面上の放物線$C$が存在することが示された。
□
本問を解答する上で考えるべきことは、$C$上の格子点を上手く(計算量が減るように)設定して、条件を満たすような整数組をいかに見つけるか(構成できることを示すか)です。とにかく題意を満たす放物線$C$が存在することを言えればよいので、「$y=77x^2$ 上に3点 $(0,\,0)$、$(1,\,77)$、$(2,\,308)$ を取ればよい」と答えるだけでも事足ります。これはいわゆる「特称命題」ならではの解答ですが、これだけでは面白くないので上記の解答例では整数問題っぽく解答しています。
条件$(1)$では「二等辺三角形にならず」という制約がありますが、これは $y=77x^2-77$ 上の $(-1,0)$、$(0,-77)$、$(1,77)$ という半ば自明な組み合わせを除外するためです。深い意味はありません。
放物線$C$の方程式を $y=77x^2+bx+c$($b,c$は任意の整数)とすれば題意を満たしそうなものですが、$y=77x^2-154x$ とすると $(0,0)$、$(1,-77)$、$(2,0)$ は二等辺三角形になってしまうので、このときは $(-1,231)$、$(0,0)$、$(1,-77)$ を頂点とする三角形などを挙げる必要があります。この点にさえ注意すれば、題意を満たすような放物線$C$と$C$上に存在する面積$77$の非二等辺三角形を無数に与えることができます。$f(x)=\pm 77x^2+bx+c$ とすれば、任意の整数$n$に対して$(n,f(n))$、$(n+1,f(n+1))$、$(n+2,f(n+2))$を頂点とする三角形の面積は常に$77$となります。このような三角形のうち二等辺三角形でないものは無数に存在し、題意を満たすような放物線$C$も無数に存在することが言えます。
なお、一般に $y=ax^2+bx+c$($b,c$は任意の整数)という方程式で表される放物線$C$について、面積が整数$a$であるような$C$上の格子点を頂点とする三角形を無数に与えることができます。$77$という数字が特別な訳ではありません。

“創作整数問題#77解法&創作整数問題#78” への2件の返信