図形の回転には複素数の積を使おう！

複素数の積には回転操作（&拡大or縮小）という図形的な意味があります。これを利用すると、ある点の周りの点や直線、曲線などの回転操作が容易に行えます。

 

---

 

 複素数の掛け算＝回転操作

複素数の掛け算は複素平面上における図形の回転操作（&拡大or縮小）に対応しています。このことを解説している参考書やウェブサイトは山のようにありますが、念のためここでも確認しておきます。

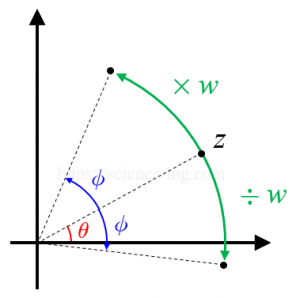
要するに、点$(x,y)$に対応する複素数 $x+yi$ に対して $\cos \varphi +i\sin \varphi$ という複素数を掛ければ、原点を中心に角$\varphi$だけ回転した点の座標が得られます。

回転中心が原点でない場合は平行移動で回転中心の点を原点に重ね合わせてから回転操作を施し、最後に平行移動で元に戻すという手順を取ります。つまり、回転を表す複素数を$w$、平行移動を表す複素数を$\alpha$とするとき、点$z$を回転して得られる点$z^{\prime }$は$$z^{\prime }=w(z+\alpha )-\alpha$$と表現できます。

 

 例題

では、いくつかの例題で使い方を確認しましょう。

求めるべき点は、複素数 $1+3i$ に対して $\cos {90}^{\circ }+i\sin {90}^{\circ }$ を掛けることで得られます。実際、$$\begin{array}{rl}& (1+3i)(\cos {90}^{\circ }+i\sin {90}^{\circ })\\ =& (1+3i)(0+i)\\ =& -3+i\end{array}$$となるので、$(-3,1)$が求める点です。

---

求めるべき点は、複素数 $1+i$ に対して $\cos {60}^{\circ }+i\sin {60}^{\circ }$ を掛ける、もしくは $\cos (-{60}^{\circ })+i\sin (-{60}^{\circ })$ を掛けることで得られます。前者の場合、$$\begin{array}{rl}& (1+i)(\cos {60}^{\circ }+i\sin {60}^{\circ })\\ =& (1+i)({\displaystyle \frac{1}{2}}+{\displaystyle \frac{\sqrt{3}}{2}}i)\\ =& {\displaystyle \frac{1-\sqrt{3}}{2}}+{\displaystyle \frac{1+\sqrt{3}}{2}}i\end{array}$$となり、後者の場合、$$\begin{array}{rl}& (1+i)(\cos (-{60}^{\circ })+i\sin (-{60}^{\circ }))\\ =& (1+i)({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\sqrt{3}}{2}}i)\\ =& {\displaystyle \frac{1+\sqrt{3}}{2}}+{\displaystyle \frac{1-\sqrt{3}}{2}}i\end{array}$$となるので、２点$(-{\displaystyle \frac{\sqrt{3}-1}{2}},{\displaystyle \frac{1+\sqrt{3}}{2}})$と$({\displaystyle \frac{1+\sqrt{3}}{2}},-{\displaystyle \frac{\sqrt{3}-1}{2}})$が求める点となります。

---

求めるべき曲線は、パラメータ表示された複素数 $t+t^{2}i$ に対して $\cos {45}^{\circ }+i\sin {45}^{\circ }$ を掛ける、もしくは $\cos (-{45}^{\circ })+i\sin (-{45}^{\circ })$ を掛けることで得られます。

前者の場合、$$\begin{array}{rl}& (t+t^{2}i)(\cos {45}^{\circ }+i\sin {45}^{\circ })\\ =& (t+t^{2}i)({\displaystyle \frac{1}{\sqrt{2}}}+{\displaystyle \frac{1}{\sqrt{2}}}i)\\ =& {\displaystyle \frac{\sqrt{2}}{2}}(t+t^{2}i)(1+i)\\ =& {\displaystyle \frac{\sqrt{2}}{2}}(t-t^2)+{\displaystyle \frac{\sqrt{2}}{2}}(t+t^2)i\end{array}$$となり、この回転操作によって移される点$(X,Y)$は$$\{\begin{array}{l}X={\displaystyle \frac{\sqrt{2}}{2}}(t-t^2)\\ Y={\displaystyle \frac{\sqrt{2}}{2}}(t+t^2)\end{array}$$と表せます。これより、$$X+Y=\sqrt{2}t$$ $$\therefore t={\displaystyle \frac{1}{\sqrt{2}}}(X+Y)$$となるので$t$を消去して整理すると、$$X^2+2XY+Y^2+\sqrt{2}X-\sqrt{2}Y=0$$を得ます。これが求める曲線の方程式となります。

また、後者の場合（$-{45}^{\circ }$だけ回転するとき）の方程式は$$X^2-2XY+Y^2-\sqrt{2}X-\sqrt{2}Y=0$$となります。

このように複素数は点だけでなく、直線や曲線といった図形の回転にも利用することができます。

 

---

---

図形の回転操作は複素平面上に落とし込んで考えるのが便利です。行列を使っても全く同じことができますが、複素数を使う方が一次変換を直感的に扱えると思います。座標平面や平面図形の問題を複素数で解くという選択肢は常に頭に入れておきたいですね！