今年の阪大数学は昨年までの難化の反動なのか、解答の方針に悩むような出題がほとんど無く、全体的に易化しました(特に文系数学が顕著です)。理系数学には複素数絡みの確率の問題があった一方、整数問題の出題はありませんでした。問題を見る限り高得点を獲得した受験生は多いと予想され、数学ではあまり差が付かなかったものと思われます。
今回は平面図形と離散数学の融合題である第3問を取り上げてみます。
《問題》
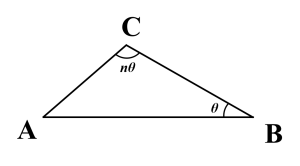
$n$を$2$以上の自然数とする。三角形$\mathrm{ABC}$において、辺$\mathrm{AB}$の長さを$c$、辺$\mathrm{CA}$の長さを$b$で表す。$\angle \mathrm{ACB}=n\angle \mathrm{ABC}$ であるとき、$c<nb$ を示せ。
(大阪大学2020年 前期理系第3問)
《考え方》
相対する辺と角が与えられているので、まずは正弦定理で関係式を作ります。不等関係を評価できそうな式が得られれば、$n$に関する数学的帰納法で片付けます。或いは別解のように適切な関数によって評価します。
● ● ●
解答例
$\angle \mathrm{ABC}=\theta$ と置く。正弦定理より、$$\dfrac{b}{\sin \theta}=\dfrac{c}{\sin n \theta}$$が成り立つから、$$c=\dfrac{\sin n \theta}{\sin \theta}b$$と表せる。よって$$\dfrac{\sin n \theta}{\sin \theta}<n \quad \cdots (*)$$を示せば題意は示される。
ここで、$\angle \mathrm{CAB}=\pi – (n+1)\theta$ であり、$\angle \mathrm{CAB}>0$ となるためには$$\pi – (n+1)\theta>0$$が必要である。故に $\theta<\dfrac{\pi}{n+1}<\dfrac{\pi}{2}$ となるから$$\cos \theta >0 \quad \cdots (**)$$となる。
以下、不等式$(*)$を数学的帰納法により示す。
$n=2$ のとき $$\frac{\sin n\theta}{\sin \theta}=\frac{\sin 2 \theta}{\sin \theta}=2 \cos \theta < 2$$より不等式$(*)$は成立する。
$n=k$ のとき不等式$(*)$が成立すると仮定すると、$$\begin{align}&(k+1)-\dfrac{\sin (k+1)\theta}{\sin \theta} \\ =&\, (k+1)-\dfrac{\sin k \theta \cos \theta+\sin \theta \cos k \theta}{\sin \theta} \\ =&\, (k+1)-\dfrac{\sin k \theta}{\sin \theta}\,\cos \theta-\cos k \theta \\ >&\, (k+1)-k\cos \theta-\cos k \theta \quad (\because (**)) \\ >&\, (k+1)-k-\cos k \theta \\ =&\, 1-\cos k \theta \ \ (> 0) \end{align}$$となり、$n=k+1$ のときも成立する。
以上より、不等式$(*)$は$2$以上のすべての整数$n$に対して成り立つ。したがって $c<nb$ が示された。
□
関数を設定して増減を調べることにより処理する方針で解いた人も多かったと思います。
別解(途中まで同じ)
不等式$(*)$を証明するには$$n \sin \theta-\sin n \theta>0$$を示せばよい。$$f(\theta)=n \sin \theta-\sin n \theta \quad \left(0 \leqq \theta<\frac{\pi}{n+1}\right)$$と置くと、$$\begin{align}f^{\prime}(\theta) &=n \cos \theta-n \cos n \theta \\ &=n(\cos \theta-\cos n \theta)\end{align}$$となる。$0<\theta<\dfrac{\pi}{n+1}$ のとき $0<\theta<n \theta<\pi$ であるから、$\cos \theta>\cos n \theta$ が成り立つ。よって$f(\theta)$は単調増加であり $f(\theta)>f(0)=0$ より、$0<\theta<\dfrac{\pi}{n+1}$ の範囲で正である。
したがって$$n \sin \theta-\sin n \theta>0$$が示されるので $c<nb$ が示された。
□
(コメント)
本問の不等式自体、なかなか面白い結果だと思います。解答上の注意としては、基本的なことですが角Bと角Cの取り違えをしないように気を付けましょう。帰納法で証明する際は $\cos \theta$ の正負についてちゃんと言及しておきましょう。因みに文系数学では $n=3$ の場合が出題されていました。
