回転対称軸が存在する立体図形の求積は、実質的には回転体の問題です。難関大を中心に時折出題されることがあるので対策は必須です。今回は千葉大学の過去問を取り上げます。出題年は20年ほど前とやや古いですが最近の入試でも十分通用する良問です。
座標空間内に2点$\mathrm{A}(1,0,0)$と$\mathrm{B}(-1,0,0)$がある。不等式$$\angle \mathrm{APB} \geqq 135^{\circ}$$をみたす空間内の点$\mathrm{P}$の全体の集合に、2点$\mathrm{A}$、$\mathrm{B}$をつけ加えてできる立体の体積を求めよ。
(2002年千葉大学前期理系 大問5)
考え方
まず平面上の場合を考えてみましょう。点$\mathrm{P}$から線分$\mathrm{AB}$を見込む角が一定であれば点$\mathrm{P}$はある円周上に存在します。また、点$\mathrm{P}$が動きうる領域は線分$\mathrm{AB}$に関して線対称になります。これを立体的に考えるのが本問です。
回転体の積分の計算がやや難しいかもしれません。図形的に処理するのが一般的ですが、置換積分を用いて計算することもできます。求積計算自体は教科書レベルなので落とせません。
解答例
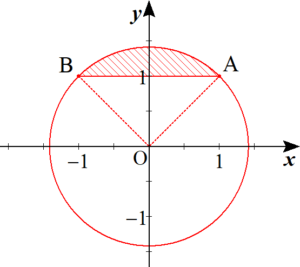
長さ$2$の線分$\mathrm{AB}$に対して $\angle \mathrm{APB} \geqq 135^{\circ}$ となる点$\mathrm{P}$の集合は、下図の斜線部分を$\mathrm{AB}$の周りに回転していられる回転体である。
円の半径は$\sqrt{2}$であり、円の方程式は $x^2+y^2=2$ となる。これは $y \geqq 0$ において $y=\sqrt{2-x^2}$ と表されるから、求める体積 $V$ は$$\begin{align} V &=\displaystyle 2 \pi \int_{0}^{1}\left(\sqrt{2-x^{2}}-1\right)^{2} d x \\ &=\displaystyle 2 \pi \int_{0}^{1}\left(3-x^{2}-2 \sqrt{2-x^{2}}\right) d x \end{align}$$となる。
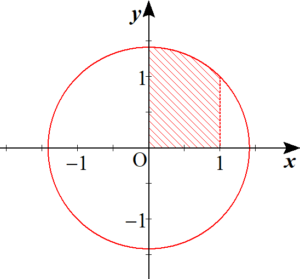
ここで$\displaystyle \int_{0}^{1}\sqrt{2-x^{2}}\,d x$ は下図の斜線部の面積に等しくなる。
これは中心角が$45^{\circ}$の扇形と夾辺が$1$の直角二等辺三角形に分割できるから、$$\begin{align} \displaystyle \int_{0}^{1} \sqrt{2-x^{2}} \, d x &=\pi(\sqrt{2})^{2} \cdot \dfrac{1}{8}+\dfrac{1}{2} \\ &=\dfrac{\pi}{4}+\dfrac{1}{2} \end{align}$$と求められる。したがって、$$\begin{align} V &=2 \pi\left\{\left[3 x-\dfrac{x^{3}}{3}\right]_{0}^{1}-2\left(\dfrac{\pi}{4}+\frac{1}{2}\right)\right\} \\ &=\color{red}{\dfrac{10}{3} \pi-\pi^{2}} \end{align}$$を得る。

本問のような回転対称性のある立体図形では、まず回転軸を含む断面を考察しましょう。なお、$\displaystyle \int_{0}^{1}\sqrt{2-x^{2}}\,d x$ は以下のように置換積分を用いて計算することもできます。$$\begin{aligned}
& \quad \ \int_{0}^{1} \sqrt{2-x^{2}} \, d x \\
&=\int_{0}^{\frac{\pi}{4}} \sqrt{2-2 \sin ^{2} \theta} \cdot \sqrt{2} \cos \theta \, d \theta \\
&=\int_{0}^{\frac{\pi}{4}} 2 \cos ^{2} \theta \, d \theta \\
&=\int_{0}^{\frac{\pi}{4}}(1+\cos 2 \theta) \, d \theta \\
&=\left[\theta+\dfrac{1}{2} \sin 2 \theta\right]_{0}^{\frac{\pi}{4}} \\
&=\dfrac{\pi}{4}+\dfrac{1}{2}
\end{aligned}$$