再び、東大理系数学から立体図形の問題をピックアップします。今回紹介する問題は空間把握が苦手な人にとってはとことん苦手なタイプと言えそうです。こういう問題にこそ「対称性の利用」が効いてきます。
$xyz$空間内の原点$\mathrm{O}(0,\,0,\,0)$を中心とし、点$\mathrm{A}(0,\,0,-1)$を通る球面を$S$とする。$S$の外側にある点$\mathrm{P}(x,y,z)$に対し、$\mathrm{OP}$を直径とする球面と$S$との交わりとして得られる円を含む平面を$L$とする、点$\mathrm{P}$と点$\mathrm{A}$から平面$L$へ下した垂線の足をそれぞれ$\mathrm{Q}$、$\mathrm{R}$とする。このとき、$$\mathrm{PQ} \leqq \mathrm{AR}$$であるような点$\mathrm{P}$の動く範囲$V$を求め、$V$の体積は$10$より小さいことを示せ。
(2002年東京大学前期理 第3問)
考え方
「球面と$S$との交わりとして得られる円」とか「平面$L$へ下した垂線」など、空間認識の苦手な人にとっては即座に捨て問認定したくなるような問題設定です。条件が少しややこしいので、しっかり問題文の内容を把握することが失点防止の第一歩です。
問題文を読むと、3点$\mathrm{O}$、$\mathrm{A}$、$\mathrm{P}$を含む平面($z$軸を含む平面)で観察すれば良さそうだと分かります。すると点$\mathrm{Q}$、$\mathrm{R}$も同じ平面上に乗っていることが分かります。なぜなら、2つの球の交わりとして得られる円(交円)の中心は$\mathrm{OP}$上に存在しており、$\mathrm{OP}$と平面$L$は直交しているからです。
あとは平面上で点と直線の距離の公式を使えばよく、点$\mathrm{P}$の動く範囲$V$が機械的に求まります。最後のおまけは$\pi$を適当な値で評価すればOK。
解答例
球面$S$が$z$軸を軸とする回転体であることに注意すると、点$\mathrm{P}$が$xz$平面上に存在するときに問題の条件をみたすならば、点$\mathrm{P}$を$z$軸のまわりに任意の角度だけ回転した点も条件をみたす。よって、$xz$平面上において点$\mathrm{P}$の動く範囲を$z$軸のまわりに1回転して得られる立体は$V$に一致する。
そこで、点$\mathrm{P}$が$xz$平面上に存在する場合を考えて$\mathrm{P}(u,\,0,\,v)$と置く。$\mathrm{OP}$を直径とする球面($S^{\prime}$とする)と$S$との交わりとして得られる円を$C$とすると、$C$の中心は線分$\mathrm{OP}$上に存在するからこのとき$xz$平面上に存在し、故に$C$の中心は点$\mathrm{Q}$に一致する。また、$\mathrm{OP}$と$\mathrm{AR}$はともに平面$L$に垂直であり、3点$\mathrm{O}$、$\mathrm{A}$、$\mathrm{P}$はいずれも$xz$平面上に存在するから点$\mathrm{R}$も$xz$平面上に存在する。以上のことから、$xz$平面上に各点および図形の断面を図示すると以下のようになる。

球面$S$および$S^{\prime}$の$xz$平面による断面は大円であり、その方程式はそれぞれ$$C_1:x^2+z^2=1$$ $$\small C_2:\left(x-\dfrac{1}{2}u\right)^2+\left(z-\dfrac{1}{2}v\right)^2=\dfrac{1}{4}(u^2+v^2)$$となる。これらの辺々の差を取って整理すると方程式$$ux+vz=1 \quad \cdots ①$$を得るが、これは$xz$平面と平面$L$との交線を表す(上図の直線)。線分$\mathrm{PQ}$、$\mathrm{AR}$は、それぞれ$\mathrm{P}$、$\mathrm{A}$から直線$①$へ下ろした垂線であるから、 $u^{2}+v^{2}>1$ であることに注意すると$$\begin{aligned}
&\mathrm{PQ}=\dfrac{u^{2}+v^{2}-1}{\sqrt{u^{2}+v^{2}}} \\
&\mathrm{AR}=\dfrac{|-v-1|}{\sqrt{u^{2}+v^{2}}}
\end{aligned}$$を得る。以下、$-v-1$ の符号によって $\mathrm{PQ} \leqq \mathrm{AR}$ を満たすような点$\mathrm{P}(u,\,0,\,v)$の条件を調べる。
(ⅰ)$-v-1 \geqq 0$ のとき、$$u^{2}+v^{2}-1 \leqq-v-1$$ $$\therefore u^{2}+\left(v+\dfrac{1}{2}\right)^{2} \leqq\left(\dfrac{1}{2}\right)^{2}$$より、これは中心が$\small \left(0,\,-\dfrac{1}{2}\right)$、半径が$\small \dfrac{1}{2}$であるような円の周および内部を表すが、これは円$C_1$の内部に含まれるので条件を満たさない。よって、このとき点$\mathrm{P}$の存在する範囲は無い。
(ⅱ)$-v-1<0$ のとき、$$ u^{2}+v^{2}-1 \leqq v+1$$ $$\therefore u^{2}+\left(v-\dfrac{1}{2}\right)^{2} \leqq\left(\dfrac{3}{2}\right)^{2}$$より、これは中心が$\small \left(0,\,\dfrac{1}{2}\right)$、半径が$\small \dfrac{3}{2}$であるような円の周および内部を表すから、このとき点$\mathrm{P}$の存在する範囲は下図の赤色斜線部のようになる。ただし円$C_1$の周および内部は除く。
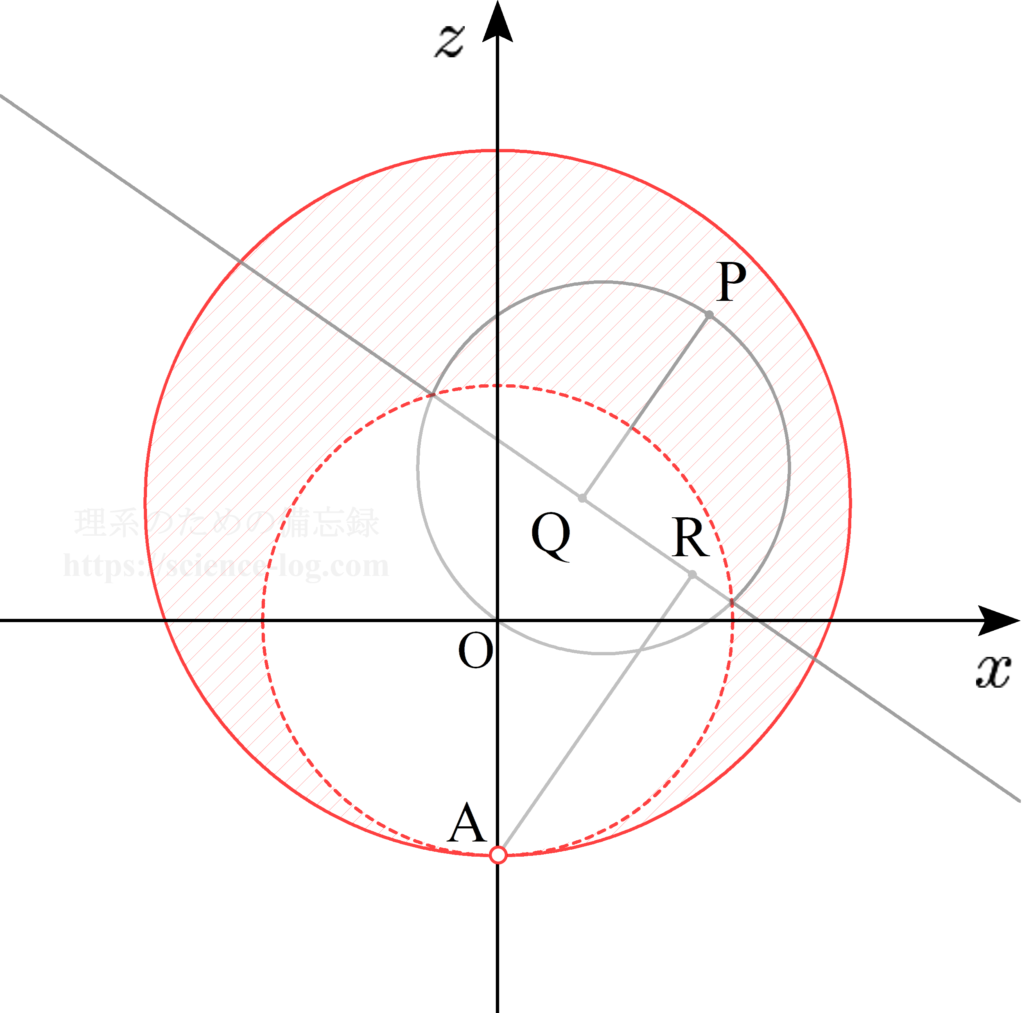
以上より$V$は、中心が$\small \left(0,\,0,\,\dfrac{1}{2}\right)$で半径が$\small \dfrac{3}{2}$であるような球の表面および内部から、中心が原点で半径が$1$であるような球の表面および内部を除いた立体となる。すなわち、$V$は連立不等式$$\color{red}{\begin{cases} x^{2}+y^{2}+\left(z-\dfrac{1}{2}\right)^{2} \leqq\left(\dfrac{3}{2}\right)^{2} \\ \text{ かつ} \\ x^{2}+y^{2}+z^{2}>1 \end{cases}}$$で表される立体である。
また、$V$の体積について、$$\small \begin{align} \dfrac{4}{3}\left\{\left(\dfrac{3}{2}\right)^{3}-1^{3}\right\} \pi &=\dfrac{19}{6} \pi \\ &<\dfrac{19}{6} \times 3.15 \\ &=9.975 \end{align}$$となるから、$V$の体積は$10$より小さいことが示された。
□

ややこしい問題設定でしたが、平面に落とし込めば決して解けない問題ではないことが体感できたと思います。最後の$\pi$の評価がやや蛇足な印象ですが(ヒントのつもり?)、これが翌年の例の円周率の問題に繋がったのかと思うと東大数学の歴史を感じますね(笑)。
円$C_2$の方程式は点$\mathrm{O}$、$\mathrm{P}$の座標を使って$$x(x-u)+z(z-v)=0$$と求めても良いでしょう。$V$の断面の図示は特に必要ありませんが、$V$が球から球をくり抜いて得られる立体であることが視覚的に説明できるので、解答時間に余裕があれば答案に書いておくと採点官に親切です。$V$を表す連立不等式の記載が無くても、どのような立体になるかを文章で正しく説明できていれば減点はありません。
ところで、問題集やウェブサイトの中には、本問について点と平面の距離の公式(「点と直線の距離の公式」の3次元版)を用いて、平面に落とし込まずに一般的に議論しているものがあります。しかし、この解法は慣れていない人にとってはフォローが難しく、また、大仰な解き方と言わざるを得ません。そんなものを持ち出さなくても解けますし、受験生が「点と平面の距離の公式」をわざわざ覚えなければならないのかと錯覚してしまいます(覚えるのは簡単ですが・・・)。
それから「点と平面の距離の公式」は平面の方程式が既知でないと使い物になりません。いま、問題設定の都合で平面$L$の法線ベクトルが分かっているので平面$L$の方程式はすぐ求めることができますが、空間ベクトルによく習熟していない人にとっては難しく回りくどいので、解法の第一選択としては個人的にお勧めしません。空間把握の苦手な人は解答例のように、各点を同一平面上に乗せて考えるのが良いと思います。
今回で5回連載してきた「実は回転体」シリーズを終了します。これまで見てきたように、問題文中では回転体であることが明示されていなくても実は回転体だと見抜ければ、対称性を利用することで計算量をグッと減らすことができます。そういった意味で、本問はこのシリーズの最後に相応しい問題でした。全ての問題の立体図形が回転軸を持つ訳ではありませんが、今後皆さんが空間図形の問題にチャレンジする際の参考になれば幸いです。