本稿では、誰もが一度は考えたことのあるであろう(?)「放物線に接する指数関数」を求めてみます。前回に引き続き「ランベルトのW関数」に登場してもらいます!
放物線と指数関数
放物線と指数関数の位置関係を考えてみます。下の図に青色が $y=x^2$、赤色が $y=a^x$($a>1$)のグラフを示します。緑色の点を左右に動かして$a$の値を変えることができます。
$a$の値を色々と変えていると、ある$a$の値でちょうど放物線と指数関数が接することが観察されます。この値は$2$にとても近い値ですが、どうやら$2$ではないようです。グラフを観察していると、大体$2.087…$くらいの微妙な数であることが分かります。
実はこの値は解析的に求めることができます。
ランベルトのW関数(再登場)
放物線と指数関数が接するためには、まず共有点を持たなければなりません。そこで、共有点の$x$座標を$t$と置きます($t$は明らかに正の実数)。
このとき、$t$は方程式$$t^2=a^t$$を満たします。このような実数$t$を求めるために、前回の「方程式$2^x=x^2$の解について」でも扱った「ランベルトのW関数」に再登場してもらいます。
ランベルトのW関数とは「関数$y=xe^x$の逆関数」のことでした。
上図のように、関数 $y=W(x)$ は $y \geqq -1$ の部分(赤色部分;$W_{0}(x)$)と $y \leqq -1$ の部分(青色部分;$W_{-1}(x)$)に分けることができます。つまり、関数 $y=W(x)$ は $-\dfrac{1}{e} \leqq x <0$ の範囲では2価関数(一つの$x$の値に対して$y$の値を$2$つ与える関数)となります。
$a$の値を求める
ランベルトのW関数についておさらいしたところで、早速、方程式を解いてみましょう。
方程式 $t^2 = a^t$ の両辺に自然対数をとり、$$2 \log |t| = t \log a$$ $$\therefore t^{-1} \log |t| = \frac{1}{2} \log a$$ $$\therefore t^{-1} \log |t| = \log \sqrt{a}$$と整理します。
いま、$t>0$ の場合を考えるので、絶対値を外すと$$t^{-1} \log t = \log \sqrt{a}$$となります。ここで $t^{-1}=e^{- \log t}$ により、$$\log t \, e^{- \log t} =\log \sqrt{a}$$ $$\therefore -\log t \, e^{- \log t} =-\log \sqrt{a}$$となります。この両辺についてランベルトのW関数をとると、$$W\left(-\log t \, e^{- \log t}\right) = W(-\log \sqrt{a})$$ $$\therefore -\log t = W(-\log \sqrt{a})$$ $$\therefore t = \color{red}{e^{-W(-\log \sqrt{a})}}$$を得ます。途中でW関数について $W(x e^x)=x$ の関係が成り立つことを利用しました。
さて、共有点の$x$座標は$e^{-W(-\log \sqrt{a})}$という値になることが分かりました。ここで、ランベルトのW関数が $-\dfrac{1}{e} \leqq x <0$ の範囲では2価関数であることを思い出して下さい。$-\log \sqrt{a}$は常に負なので、$W(x)$の2価関数の定義域内かどうかが重要となります。
$-\dfrac{1}{e} < -\log \sqrt{a} <0$ のとき、$W(-\log \sqrt{a})$は2つの値を同時に与えるため、$e^{-W(-\log \sqrt{a})}$としては2つの値が存在することになります。また、$-\log \sqrt{a}<-\dfrac{1}{e}$ のときは定義域の範囲外なので$W(-\log \sqrt{a})$の値は存在しません。
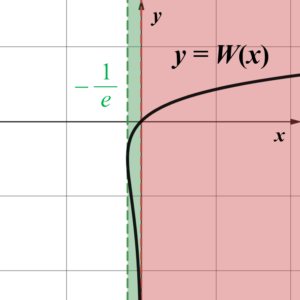
要するに、放物線と指数関数が第1象限にただ一つの共有点(特にこの場合は接線を共有する点)をもつためには、$e^{-W(-\log \sqrt{a})}$がただ一つの値を取ることが必要となります。$x<0$ の範囲で$W(x)$がただ一つの値を与えるとき、そのような負の$x$の値は$-\dfrac{1}{e}$だけなので、$a$は等式$$-\log \sqrt{a}=-\dfrac{1}{e}$$を満たすことが必要です。これを解いて$$a=e^{\frac{2}{e}}$$を得ます。これこそが求めるべき正の実数$a$の値なのでした。
あとがき
めでたく、放物線 $y=x^2$ に接する指数関数は$$y=e^{\frac{2}{e}x}$$と求められました。冒頭で述べた「$2.087…$くらいの微妙な数」の正体とは、$e^{\frac{2}{e}}$のことです。実際にこの値は$$e^{\frac{2}{e}} \approx 2.0870652286…$$という値をとります。
最後に少しだけ一般化した放物線 $y=px^2$($p>0$)に接する指数関数を考えてみます。上記の方法で同様に計算すると、そのような指数関数の式は$$y=e^{\frac{2\sqrt{p}}{e}x}$$と求めることができます。
また、$0<a<1$ の範囲では指数関数 $y=a^x$ は $a>1$ の場合と左右対称になるので、$e^{\frac{2}{e}}$の逆数をとれば同様に第2象限で接することが直ちに了解できます。
前回に引き続き「ランベルトのW関数」を使って方程式 $a^x=x^2$ の解について考察してみました。放物線に接する指数関数が解析的にきちんと求められるというのは面白い結果です。上記では特殊関数を使ってはいますが、類似した内容を扱った入試問題がどこかに出題されていても良さそうな内容ですし、誘導を付ければ大学入試の題材にもなりそうな気がします。
(2021/05/13 追記)
当サイトがいつもお世話になっているHN たけちゃん さんから、高校数学の範囲で放物線と指数関数の接点を導出する方法についてコメントを頂きました。

高校数学の範囲で,以下のように処理ができそうです.
y=x^2に対してy’=2x,y=a^x (a>1) に対してy’=(a^x)*log aだから,
2曲線がx座標tの点を共有し,かつその点における2曲線の接線が一致する条件は,
t^2=a^tかつ2t=(a^t)*log aとなって,
a^t(>0)を消去すれば,2t=t^2*log a (t≠0).
これより,容易にt=2/log a (>0)が得られ,a^t=e^2となるので,
t^2=a^t=e^2より,t=e.
a^e=e^2だから,a=(e^2)^(1/e)=e^(2/e)となりますね.
また,y=px^2は,y=(x√p)^2と表され,y=x^2をy軸を中心に,
x軸方向に1/√p倍に拡大したものであって,
a=e^(2/e)に対するy=a^xについても同様の拡大を行って,
y=a^(x√p)=(a^√p)^xに変えたものを考えれば,
y=px^2と接する指数関数のグラフを表す方程式は,
y=(e^(2/e*√p))^xとなることがわかります.
なお,この結果(というか考察の根拠)から,
放物線 y=px^2 (p>0)に,指数関数のグラフが接するとき,
接点のy座標はpによらず一定値e^2であることが従います.
たけちゃん さん
コメントありがとうございます。
確かに今回の結果は微分を使えば高校数学の範囲でもあっさり求められますね。
記事中でW関数を持ち出しましたが、牛刀割鶏とはまさにこのことですね…(笑)
ご教示頂き、ありがとうございます。