有名角・準有名角のsin・cosの値【一覧】

皆さんが三角関数を習ったときに「有名角」というものを一緒に教わったと思います。sin・cosの値がよく知られている角度としては、三角定規の角度でもある30°、45°、60°、90°などでしょうか。本稿ではその他の「準有名角」や、教科書やヘビーな参考書にすら載っていない、ほとんど誰も知らないであろう角度のsin・cosの値をご紹介！他サイトには載っていない三角比の値が満載です！

 

 有名角を少しおさらい

30°、45°、60°といった角度は日本では「有名角」と呼ばれますが、英語圏では “Important Angles” と呼ばれているようです。これらの角度は三角比を習うときに必ず登場します。その理由は$\sin$（正弦）や$\cos$（余弦）の値が非常に単純な形で表せるからです。

それぞれの値は次のようになります。

$\sin 30^{\circ}=\cos 60^{\circ}=\dfrac{1}{2}$

$\sin 45^{\circ}=\cos 45^{\circ}=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}$

$\sin 60^{\circ}=\cos 30^{\circ}=\dfrac{\sqrt{3}}{2}$

慣れてしまえばパッと出てくる値なのですが、三角比を習いたての高校1年生には少し複雑に見えるようです。これらの値は三角定規の辺の比として考えると分かりやすいのではないでしょうか。

90°以上の有名角を含めた三角比の値を１つの単位円にまとめると以下のようになります。

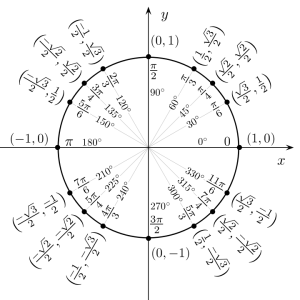
$\sin \theta$、$\cos \theta$は $0 \leqq \theta < 2\pi$ の定義域において、$-1$から$1$までの任意の実数値をとります。これは三角関数$\sin \theta$、$\cos \theta$が連続関数であることに通じるのですが、その証明で必要となる「ε-δ論法」は大学教養レベルの数学で扱われます。

有名角として知られる30°、45°、60°などは様々な入試問題（高校入試も？）で出てきますが、それ以外にも重要な角度が存在します。

 

 準有名角とは？

有名角の他に、高校数学で扱うことのある角度に15°や36°などがあります（補角はそれぞれ75°、54°です）。これらの$\sin$・$\cos$の値はそれなりに簡潔な表示をもつことが知られています。

例えば、15°であれば

$\sin 15^{\circ}=\dfrac{\sqrt{6}-\sqrt{2}}{4}$

と表され、36°なら

$\sin 36^{\circ}=\dfrac{\sqrt{10-2\sqrt{5}}}{4}$

と表すことができます。

15°の場合は$$\sin 15^{\circ} =\sin (45^{\circ} -30^{\circ})$$という関係から、加法定理を用いることで正弦の値を求めることができます。

また、36°の場合は以下のような二等辺三角形における相似比の関係から正弦の値を求めることができます。

これらの角度は「準有名角」と呼ばれることがありますが、この「準有名角」という名称はあまりメジャーではないようです。Googleで検索を掛けると「有名角」では約2億件がヒットするのに対し、「準有名角」では約300万件しかヒットしません（2018/10/16現在）。「準有名角」の検索結果の中には「有名角」のみに該当するものも含まれるため、実際に準有名角を扱っているページはもっと少ないと思われます。

半角の公式などを用いれば75°を半分にした37.5°や、45°を半分にした22.5°などの正弦・余弦の値も導出可能です。興味のある方は是非、導出にチャレンジしてみてください。

本稿では整数の角度に絞り、さらに他の角度の正弦・余弦の値について見ていきたいと思います。

 

 $\sin 3^{\circ}$は求められる？

かつて京大は後期入試に

「$\tan 1^{\circ}$は有理数か。」

という歴代最短文の問題を出題して受験業界を大いに騒がせましたが、$\tan 1^{\circ}$や$\sin 1^{\circ}$などは近似値でしか求めることができません。$\sin 1^{\circ}$を厳密に求めるには少なくとも$48$次方程式（！）の解析解を求めなければならないので、これは現実的に不可能です（ただし、もの凄く頑張れば厳密値を求めることはできます）。

一方で、その少し手前の$\sin 3^{\circ}$であれば厳密な数値が得られることが知られています。関係式$$\begin{align} \sin 3^{\circ} &= \sin (18^{\circ} -15^{\circ}) \\ &= \sin 18^{\circ} \cos 15^{\circ} – \sin 15^{\circ} \cos 18^{\circ} \end{align}$$により、15°と18°の正弦・余弦の値が既知であれば和積公式から$\sin 3^{\circ}$を求めることができます。これらの正弦・余弦の値は比較的容易に求めることができるので、$\sin 3^{\circ}$の値は高校数学の範囲で求められることが分かります。

$\sin 3^{\circ}$の値が分かったことで、加法定理や和積公式を用いることにより、$3$の倍数の整数角であれば幾らでも正弦・余弦の値を求めることができます。

因みに$\sin 3^{\circ}$を根とする最小の多項式は$16$次なので、加法定理を使わずに腕力だけで解析解を求めるというのはあまりオススメできません(笑)。

●　　　●　　　●

以下、$3$の倍数の整数角について正弦・余弦の値を列挙します。

$\small \sin 0^{\circ} = \cos 90^{\circ}= 0$

$\small \begin{align}&\sin 3^{\circ}= \cos 87^{\circ} \\ &\ \ \ =\dfrac{1}{4\sqrt{2}} \left(\dfrac{\sqrt{5} -1}{2} -\sqrt{\dfrac{3}{2} (5 + \sqrt{5})}\right) \\ &\ \ \ \ \ \ \ \ +\dfrac{1}{4\sqrt{2}} \left(\dfrac{\sqrt{3}(\sqrt{5} -1)}{2} + \sqrt{\dfrac{1}{2} (5 + \sqrt{5})}\right)\end{align}$

$\small \sin 6^{\circ}=\cos 84^{\circ}=\dfrac{1}{4}\sqrt{\dfrac{3}{2} (5 -\sqrt{5})}-\dfrac{1}{8}(\sqrt{5} + 1)$

$\small \sin 9^{\circ}=\cos 81^{\circ}=\dfrac{1+\sqrt{5}}{4\sqrt{2}}-\dfrac{\sqrt{5-\sqrt{5}}}{4}$

$\small \sin 12^{\circ}= \cos 78^{\circ}=\dfrac{1}{4}\sqrt{\dfrac{1}{2} (5 + \sqrt{5})}-\dfrac{\sqrt{3}}{8}(\sqrt{5} -1)$

$\small \sin 15^{\circ}= \cos 75^{\circ}=\dfrac{\sqrt{6}-\sqrt{2}}{4}$

$\small \sin 18^{\circ}= \cos 72^{\circ}=\dfrac{\sqrt{5}-1}{4}$

$\small \begin{align}&\sin 21^{\circ}= \cos 69^{\circ} \\ &\ \ \ =\dfrac{1}{4\sqrt{2}} \left(\sqrt{\dfrac{1}{2} (5 -\sqrt{5})}-\dfrac{\sqrt{3}(\sqrt{5} + 1)}{2}\right) \\ &\ \ \ \ \ \ \ \ +\dfrac{1}{4\sqrt{2}} \left(\sqrt{\dfrac{3}{2} (5 -\sqrt{5})}+\dfrac{\sqrt{5} + 1}{2} \right)\end{align}$

$\small \sin 24^{\circ}=\cos 66^{\circ}=\dfrac{1}{4} \sqrt{7 + \sqrt{5} -\sqrt{6(5 + \sqrt{5})}}$

$\small \begin{align}\sin 27^{\circ} &=\cos 63^{\circ} \\ &=\dfrac{1}{2} \sqrt{\dfrac{1}{2}\left(4 -\sqrt{2(5 -\sqrt{5})}\right)} \\ &=\dfrac{\sqrt{5+\sqrt{5}}}{4}+\dfrac{1-\sqrt{5}}{4\sqrt{2}}\end{align}$

$\small \sin 30^{\circ}=\cos 60^{\circ}=\dfrac{1}{2}$

$\small \begin{align}&\sin 33^{\circ}=\cos 57^{\circ} \\ &\ \ \ =\dfrac{1}{4\sqrt{2}} \left(\dfrac{\sqrt{5} -1}{2} + \sqrt{\dfrac{3}{2} (5 + \sqrt{5})}\right) \\ &\ \ \ \ \ \ \ \ +\dfrac{1}{4\sqrt{2}} \left(\dfrac{\sqrt{3}(\sqrt{5} -1)}{2}-\sqrt{\dfrac{1}{2} (5 + \sqrt{5})}\right)\end{align}$

$\small \sin 36^{\circ}=\cos 54^{\circ}=\dfrac{\sqrt{10-2\sqrt{5}}}{4}$

$\small \begin{align}&\sin 39^{\circ}=\cos 51^{\circ} \\ &\ \ \ =\dfrac{1}{4\sqrt{2}} \left(\dfrac{\sqrt{3}(\sqrt{5} + 1)}{2} + \sqrt{\dfrac{1}{2} (5 -\sqrt{5})}\right) \\ &\ \ \ \ \ \ \ \ +\dfrac{1}{4\sqrt{2}} \left(\dfrac{\sqrt{5} + 1}{2} -\sqrt{\dfrac{3}{2} (5 -\sqrt{5})}\right) \end{align}$

$\small \sin 42^{\circ}=\cos 48^{\circ}=\dfrac{1}{4}\sqrt{\dfrac{3}{2} (5 + \sqrt{5})}-\dfrac{1}{8}(\sqrt{5} -1)$

$\small \sin 45^{\circ}=\cos 45^{\circ}=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}$

$\small \sin 48^{\circ}=\cos 42^{\circ}=\dfrac{1}{4}\sqrt{\dfrac{1}{2} (5 + \sqrt{5})}+\dfrac{\sqrt{3}}{8}(\sqrt{5} -1)$

$\small \begin{align}&\sin 51^{\circ}=\cos 39^{\circ} \\ &\ \ \ =\dfrac{1}{4\sqrt{2}} \left(\dfrac{\sqrt{3}(\sqrt{5} + 1)}{2} + \sqrt{\dfrac{1}{2} (5 -\sqrt{5})}\right) \\ &\ \ \ \ \ \ \ \ +\dfrac{1}{4\sqrt{2}} \left(\sqrt{\dfrac{3}{2} (5 -\sqrt{5})} – \dfrac{\sqrt{5} + 1}{2}\right) \end{align}$

$\small \sin 54^{\circ}=\cos 36^{\circ}=\dfrac{1+\sqrt{5}}{4}$

$\small \begin{align}&\sin 57^{\circ}=\cos 33^{\circ} \\ &\ \ \ =\dfrac{1}{4\sqrt{2}} \left(\dfrac{\sqrt{5} -1}{2} + \sqrt{\dfrac{3}{2} (5 + \sqrt{5})}\right) \\ &\ \ \ \ \ \ \ \ +\dfrac{1}{4\sqrt{2}} \left(\sqrt{\dfrac{1}{2} (5 + \sqrt{5})} – \dfrac{\sqrt{3}(\sqrt{5} -1)}{2}\right) \end{align}$

$\small \sin 60^{\circ}=\cos 30^{\circ}=\dfrac{\sqrt{3}}{2}$

$\small \begin{align} \sin 63^{\circ} &=\cos 27^{\circ} \\ &=\dfrac{1}{2} \sqrt{\dfrac{1}{2}\left(4 + \sqrt{2(5 -\sqrt{5})}\right)} \\ &=\dfrac{\sqrt{5+\sqrt{5}}}{4}-\dfrac{1-\sqrt{5}}{4\sqrt{2}} \end{align}$

$\small \sin 66^{\circ}=\cos 24^{\circ}=\dfrac{1}{4}\sqrt{\dfrac{3}{2} (5 -\sqrt{5})}+\dfrac{1}{8}(\sqrt{5} + 1)$

$\small \begin{align}&\sin 69^{\circ}=\cos 21^{\circ} \\ &\ \ \ =\dfrac{1}{4\sqrt{2}} \left(\dfrac{\sqrt{3}(\sqrt{5} + 1)}{2} -\sqrt{\dfrac{1}{2} (5 -\sqrt{5})}\right) \\ &\ \ \ \ \ \ \ \ +\dfrac{1}{4\sqrt{2}} \left(\dfrac{\sqrt{5} + 1}{2} + \sqrt{\dfrac{3}{2} (5 -\sqrt{5})}\right) \end{align}$

$\small \sin 72^{\circ}=\cos 18^{\circ}=\dfrac{\sqrt{10+2\sqrt{5}}}{4}$

$\small \sin 75^{\circ}= \cos 15^{\circ}=\dfrac{\sqrt{6}+\sqrt{2}}{4}$

$\small \sin 78^{\circ}= \cos 12^{\circ}=\dfrac{1}{4}\sqrt{\dfrac{3}{2} (5 + \sqrt{5})}+\dfrac{1}{8}(\sqrt{5} -1)$

$\small \sin 81^{\circ}= \cos 9^{\circ}=\dfrac{\sqrt{5 -\sqrt{5}}}{4}+\dfrac{\sqrt{5} + 1}{4\sqrt{2}}$

$\small \sin 84^{\circ}= \cos 6^{\circ}=\dfrac{1}{4}\sqrt{\dfrac{1}{2} (5 -\sqrt{5})}+\dfrac{1}{8}(\sqrt{5} + 1)$

$\small \begin{align}&\sin 87^{\circ}=\cos 3^{\circ} \\ &\ \ \ =\dfrac{1}{4\sqrt{2}} \left(\dfrac{\sqrt{3}(\sqrt{5} -1)}{2} + \sqrt{\dfrac{1}{2} (5 + \sqrt{5})}\right) \\ &\ \ \ \ \ \ \ \ +\dfrac{1}{4\sqrt{2}} \left(\sqrt{\dfrac{3}{2} (5 + \sqrt{5})}-\dfrac{\sqrt{5} -1}{2}\right) \end{align}$

$\small \sin 90^{\circ} = \cos 0^{\circ}= 1$

これ以上はキリがないので取り敢えず$90^{\circ}$まで掲載しました。$90^{\circ}$より大きい角の$\sin$や$\cos$はこれらの値をもとに導くことができます。

 

 一応、タネ明かし（？）

度数法ではなく弧度法による表示の場合だと、同様に加法定理や倍角・半角の公式を駆使することで、$\small \sin \dfrac{\pi}{16}$ や $\small \sin \dfrac{\pi}{17}$、$\small \sin \dfrac{\pi}{24}$、$\small \sin \dfrac{\pi}{32}$ などが求められます。

実は、このように厳密に正弦・余弦の値が求められる角度というのは限られており、$a$を非負整数、$b$～$f$を$0$または$1$として、整数$n$が$$\small n = 2^a \cdot 3^b \cdot 5^c \cdot 17^d \cdot 257^e \cdot 65537^f$$と表せるときに限り、$\sin \dfrac{\pi}{n}$、$\cos \dfrac{\pi}{n}$が求められることが知られています（※注：$3$、$5$、$17$、$257$、$65537$はいずれもフェルマー素数です）。

$180=2^2 \cdot 3^{\color{red}{2}} \cdot 5$ なので、この定理によれば、やはり$\sin 1^{\circ}$や$\cos 1^{\circ}$の厳密な表示が得られないことが分かります（※注：$1^{\circ}=\dfrac{\pi}{180}$ です）。

$\sin \dfrac{\pi}{n}$、$\cos \dfrac{\pi}{n}$が求められれば幾らでも倍角の正弦・余弦の値を導くことができます。例えば $87^{\circ}=\dfrac{29}{60}\pi$ ですが、$\sin \dfrac{\pi}{60}$と$\cos \dfrac{\pi}{60}$は厳密に求められるので、$$\sin 87^{\circ} = \sin \left(\dfrac{1}{2}\pi-\dfrac{\pi}{60}\right)$$として加法定理から求めることができます。･･･などなど。

---

(2020/08/10 書式を一部変更)