今回は商学部で出題された立体図形の問題を扱います。良い問題です。

図のように、1辺の長さが$2$である立方体$ABCD$-$EFGH$の内側に、正方形$ABCD$に内接する円を底面にもつ高さ$2$の円柱$V$をとる。次の設問に答えよ。
(1)立方体の対角線$AG$と円柱$V$の共通部分として得られる線分の長さを求めよ。
(2)$W$を三角柱$ABF$-$DCG$と三角柱$AEH$-$BFG$の共通部分とする。円柱の側面と$W$の共通部分に含まれる線分の長さの最大値を求めよ。
(2021年早稲田大学(商) 第2問)
まずは自力で解いてみましょう!
考え方
(1)は「差の付く易問」といった感じの問題です。方針によって解答時間が大きく変わります。(2)は題意がやや掴みにくいですが、立体$W$によって切り取られる円柱の側面上に存在する線分の長さの最大値は何ですか、という問題です。幾何的に議論することもできますが、座標軸(角度)を設定して機械的に解くのが無難でしょう。切り取られる円柱の側面がどんな形かうまく想像できないときは、2つの三角柱を同時に考えるのではなく別々に考えてみると良いかもしれません。
解答例
(1)
立方体の対角線$AG$と円柱$V$の交点を$P$、$Q$とすると、共通部分として得られる線分は下の図の線分$PQ$に対応する。
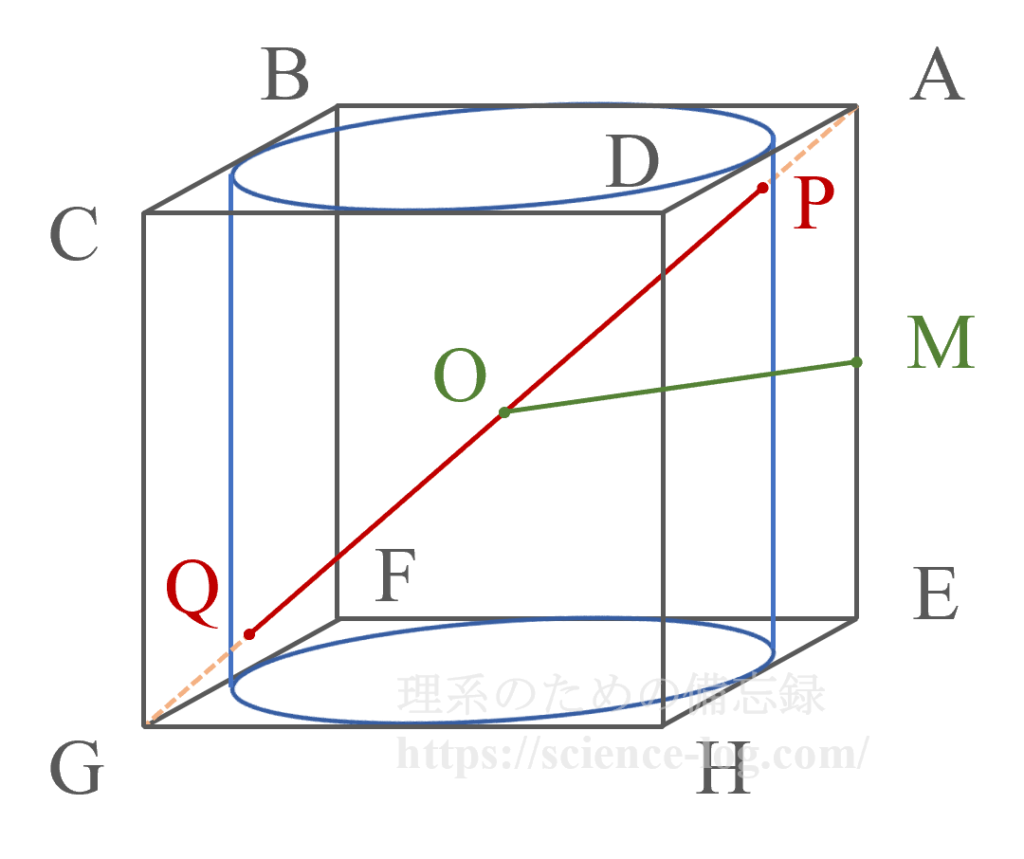
ここで、立方体の中心を$O$、線分$AE$の中点を$M$として三角形$OMA$を考える。
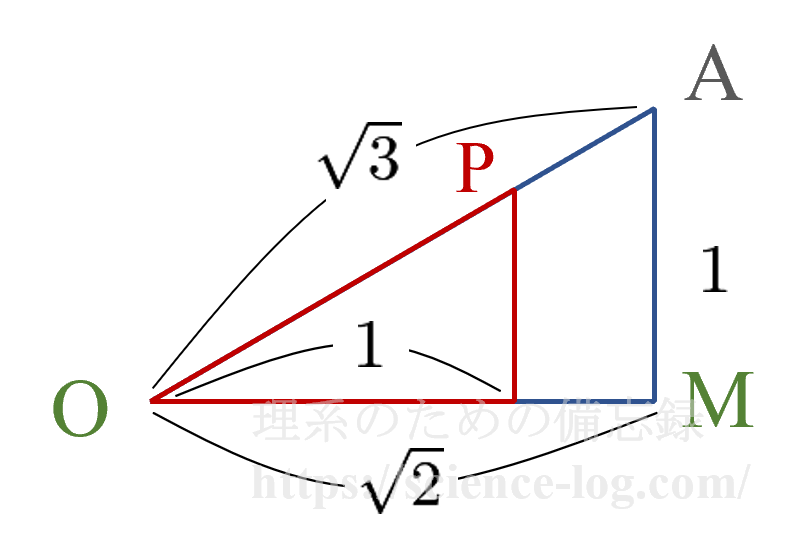
赤色、青色で示した2つの三角形は相似であるから、$$OP=1 \cdot \dfrac{\sqrt{3}}{\sqrt{2}}=\dfrac{\sqrt{6}}{2}$$と求められる。点$Q$は中心$O$に関して対称なので求める線分の長さは$OP$の2倍で、$$\color{red}{\sqrt{6}}$$である。
(2)
立体$W$は三角錐$G$-$ABF$に相当し、円柱の側面と$W$の共通部分は下図の網掛け部分の曲面となっている。
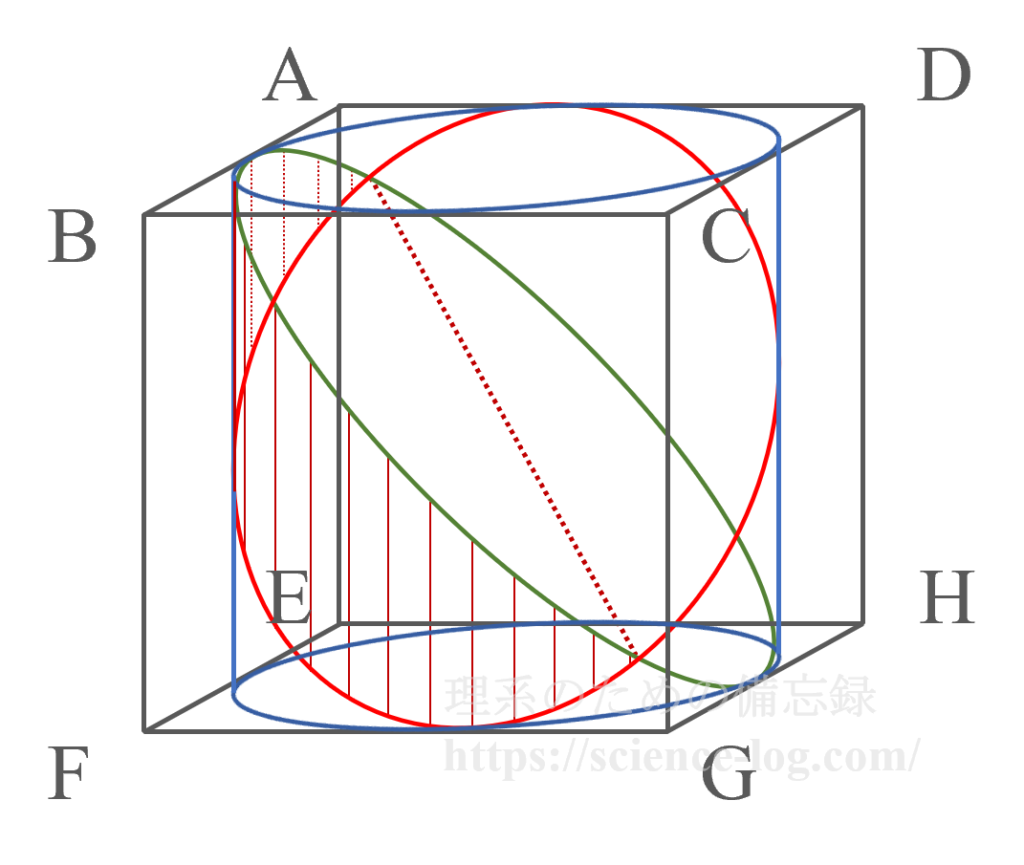 この図では四角形$AFGD$、$ABGH$による円柱の断面をそれぞれ赤色、緑色の曲線で示している。この赤色、緑色の2つの曲線をそれぞれ$C_1$、$C_2$とする。
この図では四角形$AFGD$、$ABGH$による円柱の断面をそれぞれ赤色、緑色の曲線で示している。この赤色、緑色の2つの曲線をそれぞれ$C_1$、$C_2$とする。
ここで正方形$EFGH$の中心を$O^{\prime}$、線分$GH$の中点を$M^{\prime}$とする。円柱が正方形$EFGH$と接する面の円周上に動点$I$をとり、$O^{\prime}M^{\prime}$を始線とする極座標系を考える。下図のように動径$O^{\prime}I$の偏角を$\theta$ $\left(\dfrac{3\pi}{4}<\theta<\dfrac{7\pi}{4}\right)$ とし、点$I$を通り正方形$EFGH$に垂直な直線と曲線$C_1$(赤色の曲線)、および曲線$C_2$(緑色の曲線)との交点をそれぞれ$J$、$K$とする。
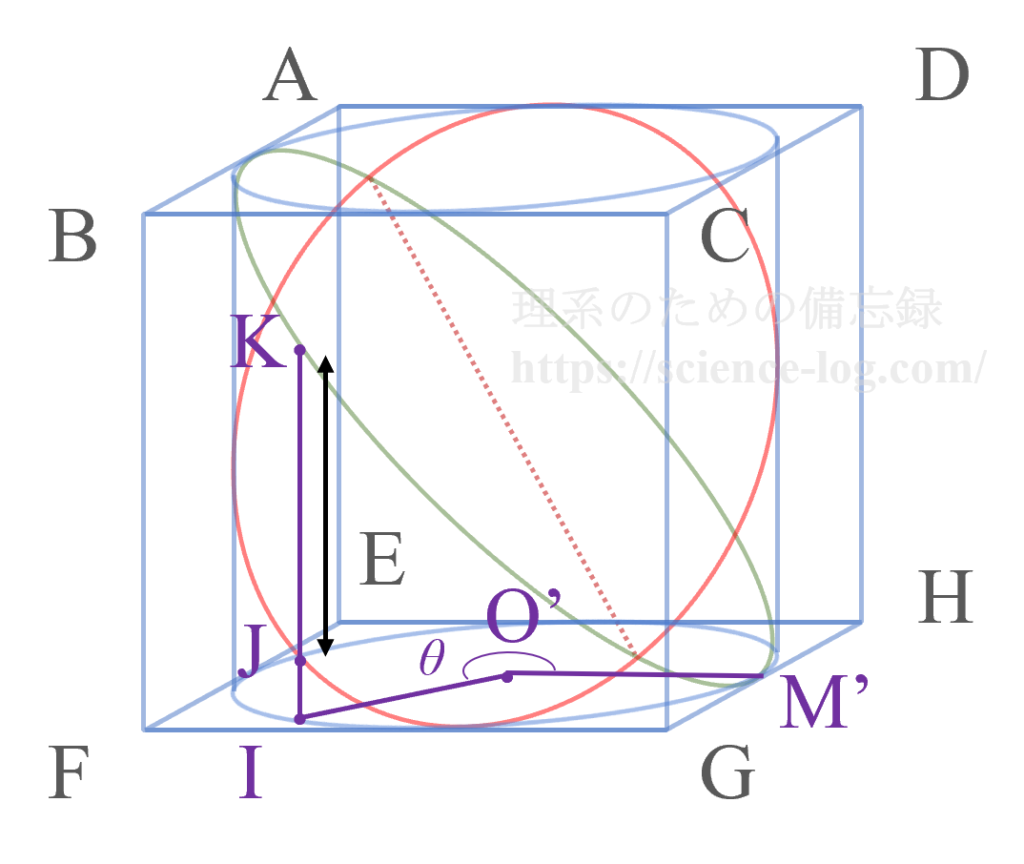
このとき、「円柱の側面と$W$の共通部分に含まれる線分の長さ」は線分$JK$の長さに相当する。いま、底面からの点$J$、$K$の高さ(距離)はそれぞれ $1+\sin \theta$、$1-\cos \theta$ となるから、$JK$の長さはこれらの差を取って $-\cos \theta-\sin \theta$ と表せる。これは合成すると $-\sqrt{2}\sin\left(\theta+\dfrac{\pi}{4}\right)$ となるから、$\left(\dfrac{3\pi}{4}<\theta<\dfrac{7\pi}{4}\right)$ の範囲における最大値は $\sqrt{2}$($\theta=\dfrac{5\pi}{4}$ のとき)である。
以上より、求める線分の長さの最大値は$$\color{red}{\sqrt{2}}$$である。

立方体の辺の長さが$2$であることを忘れて半分の値を答えてしまった人はいないでしょうか? ケアレスミスも実力のうちとはいえ、つまらないミスで失点しないように普段から注意する癖を付けましょう。
(1)は直角三角形の相似を使って片付けるのがシンプルです。多くの人は(2)で手こずったと思います。(2)は座標の設定の仕方に自由度があり、具体的な図形をある程度想像できないと答案を書きにくいタイプの問題でした。コツとしては、2つの三角柱が切断する円柱の部分を別々に考えることでしょうか。三角柱の各面に対して「どっち側に含まれるのか」を順に考えていけば、立体$W$が三角錐$G$-$ABF$を意味していることが分かるはずです。上記の解答例では角度を設定して議論していますが、空間座標を定義して3次元の不等式から機械的に考察していくこともできます。
それから、頭の中だけで想像していると気づきにくいのですが、立体$W$と円柱(中身を含む)の共通部分の立体図形には回転対称軸が存在します。この点を踏まえると、線分が対称軸を通るときに長さが最大になることが何となく見当が付きます。このことを頭の片隅に置いておけば、「真ん中」で最大となる(2)の結論が妥当であることが理解できます。
一般に、円柱の側面を展開すると断面の曲線には三角関数が現れることが知られています。実際に(2)で求められた線分長は三角関数の差になっていますよね。教科書には(多分)載っていませんが、知っているといないとでは試験の出来に差が出ることがあるので是非覚えておきたい事実です。