角の二等分線を題材とする問題は実力テストや大学入学共通テスト(旧センター試験)でも取り上げられることが多いため、しっかり対策しておきたい内容です。今回は角の二等分線の長さの導出方法に焦点を当てて解説していきます。
コンテンツ
角の二等分線の長さの公式
まず、角の二等分線の長さの公式を紹介しておきます。皆さんの教科書にも載っているかもしれません。
証明する定理
$\mathrm{BC}=a$、$\mathrm{AC}=b$、$\mathrm{AB}=c$ である$\triangle \mathrm{ABC}$について、$\angle \mathrm{A}$の二等分線と辺$\mathrm{BC}$との交点を$\mathrm{D}$とし、$\mathrm{AD}$の長さを$d$とする。
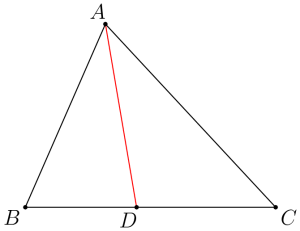
このとき $d$ について$$d^2 = \dfrac{b c} {(b+c)^2} \left((b + c)^2-a^2\right)$$が成り立つ。つまり、$\mathrm{BD}=x$、$\mathrm{CD}=y$ とすると$$d = \sqrt{bc-xy}$$となる。
補題:角の二等分線の性質
具体的な証明に入る前に、まずは次の基本的な事実を示しておきましょう。
補題
点$\mathrm{D}$が$\triangle \mathrm{ABC}$の辺$\mathrm{BC}$上に存在するとするとき、次のことは同値である。
(1)$\mathrm{AD}$は角$\angle \mathrm{BAC}$の二等分線である。
(2)$\mathrm{BD : DC = AB : AC}$

意外と示したことが無い人も多いのではないでしょうか?ここでは(1)⇒(2)の2通りの証明を示します。証明を逆から辿れば(2)⇒(1)も示せます。
» 補題の証明はこちら
補題の初等的な証明
線分$\mathrm{AD}$は$\angle \mathrm{BAC}$の二等分線とする。辺$\mathrm{BA}$の延長線上に点$\mathrm{E}$を、線分$\mathrm{AD}$と線分$\mathrm{CE}$が平行になるように取る(下図参照)。
※下の図はタップorドラッグして動かすことができます。
錯角の関係から $\angle \mathrm{ACE} = \angle \mathrm{CAD}$ であり、$\mathrm{AD}$は$\angle \mathrm{BAC}$の二等分線であるから $\angle \mathrm{CAD} = \angle \mathrm{BAD}$ であり、これより$$\angle \mathrm{DAB} = \angle \mathrm{ACE}$$が成り立つ。$\mathrm{AD}$と$\mathrm{CE}$は平行であるから $\angle \mathrm{BAD} = \angle \mathrm{AEC}$ であり、これより$$\angle \mathrm{ACE}= \angle \mathrm{AEC}$$が成り立つ。したがって$\triangle \mathrm{ACE}$は二等辺三角形であり$$\mathrm{AC} = \mathrm{AE}$$となる。$\mathrm{AD}$と$\mathrm{CE}$は平行であるから$$\mathrm{BD : DC = AB : AE}$$であり、$\mathrm{AC} = \mathrm{AE}$ より$$\mathrm{BD : DC = AB : AC}$$が成り立つ。よって示された。
□
面積公式を利用した証明も可能です。
補題の面積による証明
$\triangle \mathrm{ABD}$と$\triangle \mathrm{ACD}$は高さが等しいので面積比は底辺の長さの比と等しくなる。$$\small \begin{aligned}
\mathrm{BD}: \mathrm{DC} &=\Delta \mathrm{ABD}: \Delta \mathrm{ACD} \\
&=\dfrac{1}{2} \mathrm{AB} \cdot \mathrm{AD} \sin \angle \mathrm{BAD}: \dfrac{1}{2} \mathrm{AC} \cdot \mathrm{AD} \sin \angle \mathrm{CAD}\\
&=\mathrm{AB}: \mathrm{AC} \quad (\because \angle \mathrm{BAD}=\angle \mathrm{CAD})
\end{aligned}$$よって$$\mathrm{A B: A C=B D: D C}$$が成立する。
このとき$\triangle \mathrm{ABD}$と$\triangle \mathrm{ACD}$の面積比は$\mathrm{BD : CD}$であり、よって示された。
» 閉じる
※この補題は英語では “angle bisector theorem”(角二等分線定理)と呼ばれ、角の二等分線に関する重要な事実です。
証明①:幾何による初等的な方法
補題より、$$\begin{aligned}
\frac{\mathrm{B D}}{\mathrm{D C}} &=\frac{c}{b} \\
\therefore \frac{\mathrm{B D}}{\mathrm{D C}}+1 &=\frac{c}{b}+1 \\
\therefore \frac{\mathrm{B D+D C}}{\mathrm{D C}} &=\frac{b+c}{b} \\
\therefore \frac{a}{\mathrm{D C}} &=\frac{b+c}{b} \\
\therefore \mathrm{D C} &=\frac{a b}{b+c}
\end{aligned}$$また、これより$$\mathrm{B D} = \dfrac {a c} {b + c}$$と表されます。
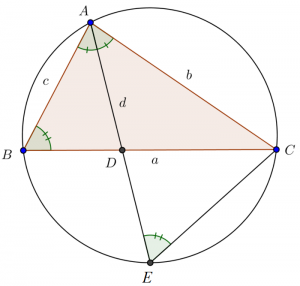
いま、仮定から $\angle \mathrm{BAD}=\angle \mathrm{EAC}$ であり、円周角の定理から $\angle \mathrm{ABD}=\angle \mathrm{AEC}$ が成り立ちます。よって$$\triangle \mathrm{ABD}∽ \triangle \mathrm{AEC}$$が言えるので、$$\mathrm{AB}:\mathrm{AD}=\mathrm{AE}:\mathrm{AC}$$より、$$\frac{c}{d}=\frac{\mathrm{AE}}{b}$$ $$\therefore \frac{c}{d}=\frac{d+\mathrm{DE}}{b}$$となります。ここで方べきの定理より、$$\mathrm{BD} \cdot \mathrm{DC} = d \cdot \mathrm{DE}$$ですから、$$\frac{c}{d} =\dfrac{d+\dfrac{\mathrm{B D \cdot D C}}{d}}{b}$$ $$\therefore b c =d^{2}+\mathrm{B D \cdot D C}$$ $$\therefore d^{2} =b c-\mathrm{B D \cdot D C}$$ $$\therefore d^{2} =b c-\frac{a c}{b+c} \cdot \frac{a b}{b+c}$$ $$\therefore d^{2} =\frac{b c}{(b+c)^{2}}\left((b+c)^{2}-a^{2}\right)$$が得られます。また、$\mathrm{BD}=x$、$\mathrm{CD}=y$ と置くと、$$\begin{aligned}
\therefore d^{2} &= b c-\frac{a c}{b+c} \cdot \frac{a b}{b+c} \\ &= bc-xy
\end{aligned}$$となります。これより、$$d=\sqrt{bc-xy}$$が示されます。
証明②:余弦定理による方法
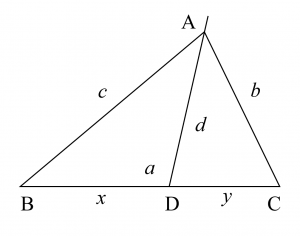
$\mathrm{AD}$は$\angle\mathrm{BAC}$の2等分線なので、補題より$$\mathrm{AB} : \mathrm{AC}=\mathrm{BD}: \mathrm{CD}$$ $$\therefore c : b =x: y$$より、$$bx=cy \quad \cdots \small{①}$$が成り立ちます。
(ⅰ)$b=c$ のとき、$\angle \mathrm{ADB}=90^{\circ}$ なので、$$d^{2}=b^{2}-x^{2}=bc-xy$$したがって、$$d=\sqrt{bc-xy}$$が成り立ちます。
(ⅱ)$b \ne c$ のとき、$\angle \mathrm{BAD}=\angle \mathrm{CAD}=\theta$ と置くと、$\triangle \mathrm{ABD}$、$\triangle \mathrm{ACD}$について余弦定理より$$\begin{cases}
\cos \theta=\dfrac{c^{2}+d^{2}-x^{2}}{2 \cdot c \cdot d} \\
\cos \theta=\dfrac{b^{2}+d^{2}-y^{2}}{2 \cdot b \cdot d}
\end{cases}$$となります。したがって、$$\frac{c^{2}+d^{2}-x^{2}}{2 \cdot c \cdot d}=\frac{b^{2}+d^{2}-y^{2}}{2 \cdot b \cdot d}$$ $$b\left(c^{2}+d^{2}-x^{2}\right)= c\left(b^{2}+d^{2}-y^{2}\right)$$ $$b d^{2}-c d^{2}=c b^{2}-b c^{2}+b x^{2}-c y^{2} \quad \cdots ②$$①より、$b x^{2}=c y \cdot x$、$c y^{2}=b x \cdot y$ となるので、これを②に代入して
$$(b-c) d^{2}=(b-c) bc-(b-c) x y$$を得ます。$b \ne c$ なので両辺を $b-c$ で割って、$$\therefore d^{2} =bc-xy$$ $$\quad d=\sqrt{bc-xy}$$を得ます。
以上、(ⅰ)および(ⅱ)より、$$d=\sqrt{bc-xy}$$が成り立ちます。
証明③:直角三角形を作る方法
あまり知られていませんが、直角三角形を作る証明法もあります。下の図はタップorドラッグして動かすことができます。
まず、$\mathrm{AB} = c$、$\mathrm{AC} = b$、$\mathrm{AD} = d$ とし、$\mathrm{AD}$は$\angle\mathrm{BAC}$の2等分線なので、補題より、$\mathrm{BD} = \dfrac {ac}{b+c}$、$\mathrm{DC} =\dfrac{ab}{b+c}$ です。
ここで$\mathrm{A}$から辺$\mathrm{BC}$に垂線を下ろし、交点を$\mathrm{E}$とします。直角三角形$\triangle \mathrm{ABE}$について$$\begin{align} c^{2} &=\mathrm{A E}^{2}+\mathrm{B E}^{2} \\ &=\mathrm{A D}^{2}-\mathrm{D E}^{2}+(\mathrm{B D+D E})^{2} \\ &= \mathrm{A D}^{2}+\mathrm{B D}^{2}+2 \mathrm{B D} \cdot \mathrm{D E} \end{align}$$となるから、関係式$$(1)\quad 2 \mathrm{B D} \cdot \mathrm{D E}=c^{2}-\mathrm{A D}^{2}-\mathrm{B D}^{2}$$を得ます。
ここで直角三角形$\triangle \mathrm{ACE}$について$$\begin{align} b^{2} &=\mathrm{A E}^{2}+\mathrm{C E}^{2} \\ &=\mathrm{A D}^{2}-\mathrm{D E}^{2}+(\mathrm{CD-D E})^{2} \\ &= \mathrm{A D}^{2}+\mathrm{CD}^{2}-2 \mathrm{CD} \cdot \mathrm{D E} \end{align}$$となるから、関係式$$(2)\quad 2 \mathrm{CD} \cdot \mathrm{DE}=\mathrm{AD}^{2}-\mathrm{CD}^{2}-b^{2}$$を得ます。
$(1)$と$(2)$より、辺々の比をとって整理すると$$\dfrac{\mathrm{BD}}{\mathrm{CD}}=\dfrac{c^{2}-\mathrm{AD}^{2}-\mathrm{BD}^{2}}{\mathrm{AD}^{2}+\mathrm{CD}^{2}-b^{2}}$$ $$\therefore \dfrac{c}{b}=\dfrac{c^{2}-d^{2}-\left(\dfrac{a c}{b+c}\right)^{2}}{d^{2}+\left(\dfrac{a b}{b+c}\right)^{2}-b^{2}}$$ $$\therefore \small d^{2}(b+c)=b c^{2}-b \cdot\left(\frac{a c}{b+c}\right)^{2}+b^{2} c-c \cdot\left(\frac{a b}{b+c}\right)^{2}$$ $$\therefore d^{2}(b+c)=b c(b+c)-\dfrac{a^{2} b c}{b+c}$$ $$\therefore d^{2}=b c-\dfrac{a^{2} b c}{(b+c)^{2}}$$ $$\therefore d^{2} =\frac{b c}{(b+c)^{2}}\left((b+c)^{2}-a^{2}\right)$$が得られます。
これより、$\mathrm{BD}=x$、$\mathrm{CD}=y$ と置くと、$$\begin{aligned}
\therefore d^{2} &= b c-\frac{a c}{b+c} \cdot \frac{a b}{b+c} \\ &= bc-xy
\end{aligned}$$となるので、$$d=\sqrt{bc-xy}$$が示されます。
※直角三角形を作って証明する方法はこの他にも3つくらい知られているのですが、式変形で簡単に解決できるものを掲載しました。その他の初等的な証明についてはスリランカの数学者であるAmarasinghe氏の論文(外部リンク)が詳しいです。
証明④:スチュワートの定理による方法
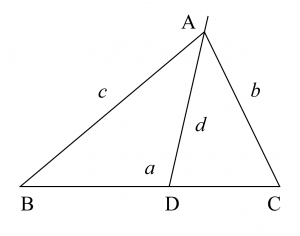
スチュワートの定理より、$$\small b^2 \cdot \mathrm{BD} + c^2 \cdot \mathrm{DC} = d^2 \cdot a + \mathrm{BD} \cdot \mathrm{DC} \cdot a$$という関係式が成り立ちます。$\mathrm{BD} = \dfrac {ac}{b+c}$、$\mathrm{DC} =\dfrac{ab}{b+c}$ より、$$b^{2} \cdot \frac{a c}{b+c}+c^{2} \cdot \frac{a b}{b+c} =d^{2} \cdot a+\frac{a c}{b+c} \cdot \frac{a b}{b+c} \cdot a$$ $$\therefore a b c \cdot \frac{b+c}{b+c} =d^{2} \cdot a+\frac{a^{2} b c}{(b+c)^{2}} \cdot a$$ $$\therefore b c =d^{2}+\frac{a^{2} b c}{(b+c)^{2}}$$ $$\therefore d^{2} =b c\left(1-\frac{a^{2}}{(b+c)^{2}}\right)$$ $$\therefore d^{2} =\frac{b c}{(b+c)^{2}}\left((b+c)^{2}-a^{2}\right)$$が得られます。
これより、$\mathrm{BD}=x$、$\mathrm{CD}=y$ と置くと、$$\begin{aligned}
\therefore d^{2} &= b c-\frac{a c}{b+c} \cdot \frac{a b}{b+c} \\ &= bc-xy
\end{aligned}$$となるので、$$d=\sqrt{bc-xy}$$が示されます。
※スチュワートの定理は余弦定理から簡単に証明できます。導出の原理さえ知っていればスチュワートの定理を公式として覚えておく必要はありません。

以上、4種類の証明法を紹介してきました。ベクトルを使っても証明できそうですが、内積を上手く処理しなければならず、ベクトルだけで押し切るのは難しそうです。
$\vec{b}=\vec{\mathrm{AB}}$、$\vec{c}=\vec{\mathrm{AC}}$、$\vec{d}=\vec{\mathrm{AD}}$ と置くと、点$\mathrm{D}$は角$\angle \mathrm{BAC}$の二等分線と辺$\mathrm{BC}$との交点なので、$$\vec{d}=\dfrac{|\vec{c}| \vec{b}+|\vec{b}| \vec{c}}{|\vec{b}|+|\vec{c}|}\quad \cdots (*)$$と表されます。$\mathrm{BD}=x=\dfrac{|\vec{c}|}{|\vec{b}|+|\vec{c}|}$、$\mathrm{CD}=y=\dfrac{|\vec{b}|}{|\vec{b}|+|\vec{c}|}$ なので$(*)$は$$\vec{d}=x\vec{b}+y\vec{c}$$と書き換えることができますが、ここからの式変形には工夫が要りそうです。