関数f(sinx)に関する考察

ふとしたことから$f(x)$に$\sin x$を代入した形の合成関数について考察する機会があったので、まとめてみます。

 

 $f(x)$ が3次関数のとき

$$\begin{array}{rl}{\displaystyle \frac{d}{dx}}f(\sin x)& =(\sin x{)}^{\prime }{f}^{\prime }(\sin x)\\ & =\cos x{f}^{\prime }(\sin x)\end{array}$$となるから、$f(x)=x^3+ax$ のとき $f^{\prime }(x)=3x^2+a$ より、$${\displaystyle \frac{d}{dx}}{f}^{\prime }(\sin x)=(3{\sin }^{2}x+a)\cos x$$と求められます。

このとき$f(\sin x)$が $x={\displaystyle \frac{\pi }{2}}+n\pi$（$n$は整数）で極値をもつのは$\cos x$が掛かっていることから明らかです。また、$-3<a<0$ のとき、$\sin x=\pm \sqrt{-{\displaystyle \frac{a}{3}}}$ を満たすような実数$x$が無数に存在します。

簡単のために $0<x<\pi$ の範囲に限定して考えてみます。$-3<a<0$ のとき、$\sin A=\sqrt{-{\displaystyle \frac{a}{3}}}$ を満たすような実数 $x=A$ は $0<x<\pi$ の範囲に２つ存在します^*1。

$-3<a<0$ のときグラフを描くと以下のようになります。右側の縦破線は $x=\pi$ の直線です。

 

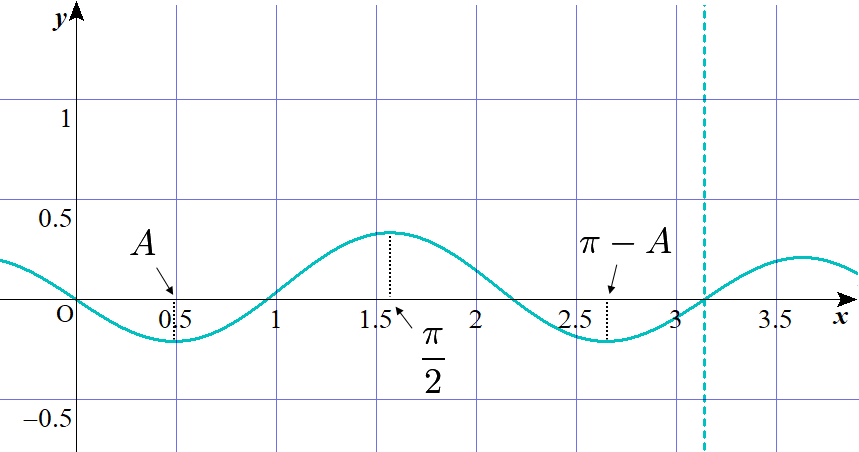
 $f(\sin x)$ の対称性と周期性

グラフを見ても分かる通り、$y=f(\sin x)$ は $x={\displaystyle \frac{\pi }{2}}+n\pi$ に関して対称(線対称)です。このことを示すには ${\displaystyle \frac{\pi }{2}}-x$ などを $y=f(\sin x)$ に代入して$f(\sin ({\displaystyle \frac{\pi }{2}}+x))$に一致することを確かめればOKです。

実際、$$f(\sin ({\displaystyle \frac{\pi }{2}}-x))=f(\cos x)=f(\sin ({\displaystyle \frac{\pi }{2}}+x))$$となるので、同様にして $x={\displaystyle \frac{\pi }{2}}+n\pi$ に関して $y=f(\sin x)$ が対称であることが示されます。

そもそも $y=\sin x$ が $x={\displaystyle \frac{\pi }{2}}+n\pi$ に関して対称なので自明と言えば自明なことです。

 

 $f(\sin x)$ の積分

$f(x)$が何らかの多項式であれば、原理的には積分可能です。例えば $f(x)=x^3+ax$ のとき、$$\begin{array}{rl}& \int ({\sin }^{3}x+a\sin x)dx\\ =& \int \{\sin x(1-{\cos }^{2}x)+a\sin x\}dx\\ =& -\cos x+\frac{1}{3}{\cos }^{3}x-a\cos x+C\end{array}$$となります。

$y=f(\sin x)(0\leqq x\leqq \pi )$ と $y=0$ の囲む図形のうち第1象限にあるものの面積を$S_1$、第4象限にあるものの面積の和を$S_2$とするとき、$S_1=S_2$ となるのは、実数$a$が$${[-\cos x+\frac{1}{3}{\cos }^{3}x-a\cos x]}_0^{\pi }=0$$を満たすときなので、これを計算して $a=-{\displaystyle \frac{2}{3}}$ という値を得ます。

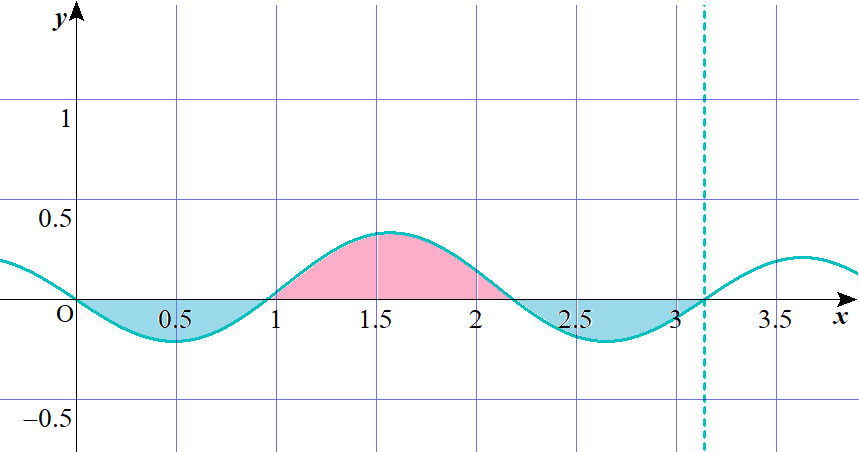
$y=f(\sin x)$ は $x={\displaystyle \frac{\pi }{2}}$ に関して対称なので、上記の話は $0\leqq x\leqq {\displaystyle \frac{\pi }{2}}$ の範囲についても言えます。

 

 $f(\sin x)$ の積分と点対称性

連続関数$f(x)$に対して一般に$${\displaystyle {\int }_0^{\pi }xf(\sin x)dx={\displaystyle \frac{\pi }{2}}{\displaystyle {\int }_0^{\pi }f(\sin x)dx}}$$という関係式が成り立ちます。これにより、不定積分が求められない関数であっても定積分なら計算可能となる場合があります。

$x=\pi -t$ とおくと $dx=-dt$、$$\begin{array}{rccc}x& 0& \to & \pi \\ t& \pi & \to & 0\end{array}$$より、$$\begin{array}{rl}{\int }_0^{\pi }xf(\sin x)dx& ={\int }_{\pi }^0(\pi -t)f(\sin (\pi -t))(-dt)\\ & ={\int }_0^{\pi }(\pi -t)f(\sin t)dt\\ & =\pi {\int }_0^{\pi }f(\sin t)dt-{\int }_0^{\pi }tf(\sin t)dt\\ & =\pi {\int }_0^{\pi }f(\sin x)dx-{\int }_0^{\pi }xf(\sin x)dx\end{array}$$となるので、$$\therefore {\displaystyle {\int }_0^{\pi }xf(\sin x)dx={\displaystyle \frac{\pi }{2}}{\displaystyle {\int }_0^{\pi }f(\sin x)dx}}$$の成立が示されます。

この関係式には図形的な意味があります。ここで $F(x)=(x-{\displaystyle \frac{\pi }{2}})f(\sin x)$ と置くと、$$\begin{array}{rl}F(\pi -x)& =\{(\pi -x)-\frac{\pi }{2}\}f(\sin (\pi -x))\\ & =-(x-\frac{\pi }{2})f(\sin x)\\ & =-F(x)\end{array}$$となるので、$F(x)$は点$({\displaystyle \frac{\pi }{2}},0)$に関して対称であることが言えます。そこで $0<x<\pi$ の範囲で積分をとれば、$${\displaystyle {\int }_0^{\pi }(x-{\displaystyle \frac{\pi }{2}})f(\sin x)dx=0}$$となるので、$${\displaystyle {\int }_0^{\pi }xf(\sin x)dx={\displaystyle \frac{\pi }{2}}{\displaystyle {\int }_0^{\pi }f(\sin x)dx}}$$が導かれます。

例えば $f(\sin x)={\sin }^{4}x+3{\sin }^{3}x$ のとき、$y=(x-{\displaystyle \frac{\pi }{2}})f(\sin x)$ のグラフを描くと次のようになります。

図中の縦破線は $x={\displaystyle \frac{\pi }{2}}$ の直線です。点対称なので当然、灰色網掛け部分の面積は等しくなります。

この関係式を利用すれば$${\displaystyle {\int }_0^{\pi }{\displaystyle \frac{x{\sin }^{2}x}{{\sin }^{3}x+8}}dx}$$などの値が計算できます^*2。

 

 $f(\sin x)$ と $f(\cos x)$ の関係

一般に$${\displaystyle {\int }_0^{\pi /2}f(\sin x)dx={\int }_0^{\pi /2}f(\cos x)dx}$$が成立します。これは$$\{\begin{array}{l}\sin ({\displaystyle \frac{\pi }{2}}-x)=\cos x\\ \cos ({\displaystyle \frac{\pi }{2}}-x)=\sin x\end{array}$$を用いて容易に示されます。

 

---

点対称性を意識した問題は稀に入試に出題されることがあります。知らなくても解答に差し支えはありませんが、知っていると少しトクした気分になれる…はず。

---

*1. ^  $0<A<{\displaystyle \frac{\pi }{2}}$ とすれば $A={\sin }^{-1}\sqrt{-{\displaystyle \frac{a}{3}}}$ と表すこともできます。

*2. ^  2010年に横浜国立大学の前期理系第1問に誘導付きで出題があります。