本稿では1次関数と指数関数の交点を求め、1次関数が指数関数の接線になる条件についても調べてみます。またまた今回も「ランベルトのW関数」が登場します。
指数関数と直線
$a>0$ かつ $a \ne 1$ であるような実数$a$に関して $y=a^x$ という式で表される関数は「指数関数」と呼ばれます。指数関数は現行課程の高校数学だと数Ⅱの範囲で習う内容で、入試問題としても頻繁に出題されますが、1次関数や2次関数と指数関数の交点を求めさせる問題が出題されることはほとんどありません。何故かというと、一般に指数関数と多項式関数の交点は初等的に表現することができないからです。
簡単な例で見てみましょう。下の図のように1次関数 $y=2x+1$ と指数関数 $y=2^x$ は2点で交わります。交点の一つが$(0,\,1)$であることはグラフから明らかですね。もう一方の交点の$x$座標の近似値は $x \approx 2.659861…$ となり、$$2 \times 2.659861… +1=2^{2.659861…}$$という関係式が成り立ちます。実は、この座標の厳密な値は高校数学の範囲で表現することができません。
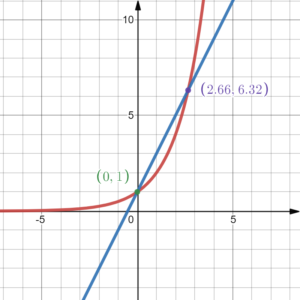
ある直線 $y=px+q$ と、ある指数関数 $y=a^x$ が交わるということは、これらのグラフが共有点を持つことを意味します。そこで共有点の$x$座標を$t$と置けば、$t$は方程式$$pt+q=a^t$$を満たします。このような実数$t$が存在するかどうかを調べるために「ランベルトのW関数」という特殊関数を使います。
ランベルトのW関数(再々登場)
前回の「放物線に接する指数関数を求めてみよう」や前々回の「方程式$2^x=x^2$の解について」の記事でも扱った「ランベルトのW関数」にまたしても登場してもらいます。
ランベルトのW関数とは「関数$y=xe^x$の逆関数」のことでしたね。
上図のように、関数 $y=W(x)$ は $y \geqq -1$ の部分(赤色部分;$W_{0}(x)$)と $y \leqq -1$ の部分(青色部分;$W_{-1}(x)$)に分けることができます。つまり、関数 $y=W(x)$ は $-\dfrac{1}{e} \leqq x <0$ の範囲では2価関数(一つの$x$の値に対して$y$の値を$2$つ与える関数)となります。
指数関数と直線の交点
W関数について $W(x e^x)=x$ という関係式が成り立つことを利用して方程式$$px+q=a^x$$を解いていきます。$a^x=e^{x\log{a}}$ と書き換えられるので、$$px+q=e^{x\log{a}}$$ $$(px+q)e^{-x\log{a}}=1$$両辺に$-\dfrac{1}{p}\log{a}$を掛けて$$\left(-x\log{a}-\dfrac{q}{p}\log{a}\right)e^{-x\log{a}}=-\dfrac{1}{p}\log{a}$$ $e^{-\frac{q}{p}\log{a}}=a^{-\frac{q}{p}}$を両辺に掛けて$$\left(-x\log{a}-\dfrac{q}{p}\log{a}\right)e^{-x\log{a}-\frac{q}{p}\log{a}}=-\dfrac{a^{-\frac{q}{p}}}{p}\log{a}$$を得ます。ここで両辺についてランベルトのW関数をとると、$$-x\log{a}-\dfrac{q}{p}\log{a}=W\left(-\dfrac{a^{-\frac{q}{p}}}{p}\log{a}\right)$$より、$$x=\color{red}{-\dfrac{1}{\log{a}}W\left(-\dfrac{a^{-\frac{q}{p}}}{p}\log{a}\right)-\dfrac{q}{p}}$$を得ます。これが求めるべき一般解です。
先ほど、ランベルトのW関数は $-\dfrac{1}{e} \leqq x <0$ の範囲で2価関数であることを説明しました。つまり括弧内の $-\dfrac{a^{-\frac{q}{p}}}{p}\log{a}$ の値によって共有点の$x$座標の個数が決まります。
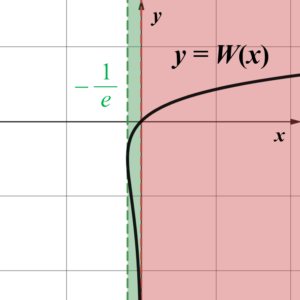
$0 \leqq -\dfrac{a^{-\frac{q}{p}}}{p}\log{a}$ のとき(薄赤色の領域)、$W(-\dfrac{a^{-\frac{q}{p}}}{p}\log{a})$は1つの値をとるので指数関数と直線の交点は1個だけ存在します。
$-\dfrac{1}{e} < -\dfrac{a^{-\frac{q}{p}}}{p}\log{a} <0$ のとき(緑色の領域)、$W(-\dfrac{a^{-\frac{q}{p}}}{p}\log{a})$は2つの値を同時に与えるため、指数関数と直線の交点は2個存在することになります。
$-\dfrac{a^{-\frac{q}{p}}}{p}\log{a}=-\dfrac{1}{e}$ のとき(緑色の領域の左端)、$W(-\dfrac{a^{-\frac{q}{p}}}{p}\log{a})$は1つの値をとるので指数関数と直線の交点は1個だけ存在します。このとき特に、1次関数 $y=px+q$ は指数関数 $y=a^x$ の接線となります。
また、$-\dfrac{a^{-\frac{q}{p}}}{p}\log{a}<-\dfrac{1}{e}$ のとき(無色の領域)は定義域の範囲外なので$W(-\dfrac{a^{-\frac{q}{p}}}{p}\log{a})$の値は存在しません。つまり、このとき指数関数と直線の交点は存在しません。
指数関数の接線になる条件
上記で$$(*)\quad -\dfrac{a^{-\frac{q}{p}}}{p}\log{a}=-\dfrac{1}{e}$$が成り立つとき、1次関数 $y=px+q$ は指数関数 $y=a^x$ の接線になると述べましたが、果たして本当でしょうか?
ここで$a$を定数として、$(*)$式を$q$について解いてみましょう。$$-\dfrac{a^{-\frac{q}{p}}}{p}\log{a}=-\dfrac{1}{e}$$ $$\therefore a^{-\frac{q}{p}}=\dfrac{p}{e\log{a}}$$ $$\therefore a^{q}=\left(\dfrac{e\log{a}}{p}\right)^{p}$$両辺に自然対数をとって$$q \log a=p\log\left(\dfrac{e\log{a}}{p}\right)$$ $$\therefore q=\dfrac{p}{\log{a}}\log\left(\dfrac{e\log{a}}{p}\right)$$を得ます。
これより、1次関数$$y=px+\dfrac{p}{\log{a}}\log\left(\dfrac{e\log{a}}{p}\right)$$は指数関数 $y=a^x$ の接線になります。そのときのグラフを下に示します。緑色、橙色の点を左右にスライドすれば、それぞれ$a$、$p$の値を動かせます。
確かに接線になっていることが分かりますね!
これは導関数を用いて接線の方程式を導いても全く同じ式が得られることからも理解できます。計算練習がてら、検算してみて下さい。

3回連続で指数関数に関する話題を扱ってみました。少しは「ランベルトのW関数」に親しみを感じられるようになってきたでしょうか?(笑)
$y=2^x$ と $y=2x$ などといった特殊な場合を除いて、一般の指数関数と直線の交点の座標は高校数学の範囲では与えることはできません。一般には今回紹介したようにランベルトのW関数を用いて表現することになります。
ここ3回にわたって紹介した指数関数についての話題は、普通の高校生で知っている人は少ない内容だと思います。意欲的な学生向けの教材として授業で扱ってみると色々と発見があって面白いかもしれません。