関西大学の入試問題から正弦の逆数の微積分に関する問題を取り上げます。
《問題》
曲線 $C: y=\dfrac{1}{\sin 2 x}\ \left(0<x<\dfrac{\pi}{2}\right)$ と直線 $\ell: y=2$ で囲まれる図形を$K$とする。
(1)関数 $f(x)=\dfrac{1}{\sin 2 x}$ の導関数 $f'(x)$ を求めよ。また $0<x<\dfrac{\pi}{2}$ における$f(x)$の極値を求めよ。
(2)曲線 $C$ と直線 $\ell$ の交点の $x$ 座標を求めよ。
(3)不定積分 $\displaystyle \int \dfrac{1}{\sin 2 x} d x$ を求めよ。
(4)図形 $K$ の面積 $S$ を求めよ。
(関西大学2020年 理系(2/5 3教科型)第1問)
《考え方》
誘導が丁寧です。(1)で曲線 $C$ の概形を把握し、(2)で積分範囲を求めます。ここまでは特に問題無く進められるはずです。問題は(3)でしょうか。$\displaystyle \int \dfrac{1}{\sin x} d x$ の不定積分についてはこちらのページで詳しく解説していますので、積分計算に詰まってしまった方は急いで確認しましょう!
解答例
(1)
$$\small \begin{aligned}
f^{\prime}(x) &=\frac{-(\sin 2 x)^{\prime}}{\sin ^{2} 2 x} \\
&=\color{red}{-\frac{2 \cos 2 x}{\sin ^{2} 2 x}} \quad \cdots (\text{答})
\end{aligned}$$より、増減表は次のようになる。$$\small \begin{array}{|c|c|c|c|c|c|}
\hline x & (0) & \cdots & \dfrac{\pi}{4} & \cdots & \left(\dfrac{\pi}{2}\right) \\
\hline f^{\prime}(x) & & – & 0 & + & \\
\hline f(x) & & \searrow & 1 & \nearrow & \\
\hline \end{array}$$これより、$f(x)$は $x=\dfrac{\pi}{4}$ において極小値$$\color{red}{1} \quad \cdots (\text{答})$$をとる。
(2)
$$\small \frac{1}{\sin 2 x}=2$$ $$\small \therefore \sin 2 x=\frac{1}{2}$$ $$\small \therefore x=\frac{1}{12} \pi, \frac{5}{12} \pi \ \left(\because 0<x<\frac{\pi}{2}\right)$$より、求める交点の $x$ 座標は$$x=\color{red}{\frac{1}{12} \pi, \frac{5}{12} \pi} \quad \cdots (\text{答})$$となる。
(3)
$$\small \begin{aligned}
& \quad \int \frac{1}{\sin 2 x} d x \\ &=\int \frac{\sin 2 x}{\sin ^{2} 2 x} d x \\
&=\int \frac{\sin 2 x}{1-\cos ^{2} 2 x} d x \\
&=\frac{1}{2} \int\left(\frac{1}{1-\cos 2 x}+\frac{1}{1+\cos 2 x}\right) \sin 2 x \,d x \\
&=-\frac{1}{4} \int\left\{\frac{(\cos 2 x)^{\prime}}{1-\cos 2 x}+\frac{(\cos 2 x)^{\prime}}{1+\cos 2 x}\right\} d x \\
&=-\frac{1}{4}\{-\log |1-\cos 2 x|+\log |1+\cos 2 x|\}+C \\
&=\color{red}{\frac{1}{4} \log \left|\frac{1-\cos 2 x}{1+\cos 2 x}\right|+C} \quad \cdots (\text{答})
\end{aligned}$$
(4)
(1)と(2)の結果より、図形 $K$ は以下の斜線部である。
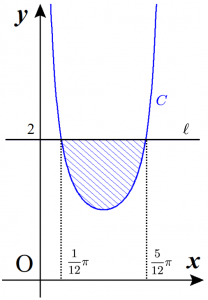
(3)の結果を利用すると、面積は$$\small \begin{aligned}
S &=\int_{\frac{1}{12}\pi}^{\frac{5}{12}\pi}\left(2-\frac{1}{\sin 2 x}\right) d x \\
&=\left[2 x-\frac{1}{4} \log \left|\frac{1-\cos 2 x}{1+\cos 2 x}\right|\right]_{\frac{1}{12}\pi}^{\frac{5}{12} \pi} \\
&=\frac{2}{3} \pi-\frac{1}{4}\left\{\log \left(\frac{1-\cos \frac{5}{6} \pi}{1+\cos \frac{5}{6} \pi}\right)-\log \left(\frac{1-\cos \frac{1}{6} \pi}{1+\cos \frac{1}{6} \pi}\right)\right\} \\
&=\frac{2}{3} \pi-\frac{1}{4}\left\{\log \left(\frac{2+\sqrt{3}}{2-\sqrt{3}}\right)-\log \left(\frac{2-\sqrt{3}}{2+\sqrt{3}}\right)\right\} \\
&=\frac{2}{3} \pi-\frac{1}{4}\left\{\log (2+\sqrt{3})^{2}-\log (2-\sqrt{3})^{2}\right\} \\
&=\frac{2}{3} \pi-\frac{1}{2} \log \left(\frac{2+\sqrt{3}}{2-\sqrt{3}}\right) \\
&=\color{red}{\frac{2}{3} \pi-\log (2+\sqrt{3})} \quad \cdots (\text{答})
\end{aligned}$$と求められる。
(コメント)
(3)の不定積分の計算はしっかりマスターしておくべきです。計算結果はできるだけ簡単かつコンパクトになるように式変形しましょう。
