国際信州学院大学2017年数学解説（理）

夏の暑さを思わせる天気が続く今日この頃です。湿度がそこまで高くないだけマシかもしれませんが、今年は梅雨入りが例年より早いみたいですね。

今回は最近ネット界隈でメジャーになってきた国際信州学院大学の「過去問」を取り上げます！（但し、とても試験時間75分で解けるような内容ではありません(笑)）

 

 第1問

（国際信州学院大学2017年　第１問）

---

小問に分かれてはいますが特に脈絡は無いと思われます。というよりも、本問はマジメに解こうとして解ける問題ではありません(笑)。

（１）

条件より、$n$は素数である。$n=2$ のとき $n^2+4$ は$2$以上の偶数となるので素数でない。故に$n$は$3$以上の奇素数であることが必要となる。･･･。

●　　　●　　　●

実は次のような予想が知られています。

『Bunyakovsky予想』 係数が整数で、最高次の係数が正であるような2次以上の既約多項式は、すべての自然数に対して、1より大きな最大公約数を持つ無限集合、もしくは無限個の素数を生成する

この「ブニャコフスキー予想」はウクライナの数学者ヴィクトール・ブニャコフスキーが1857年に提示した予想なのですが、未だに完全な証明が与えられていません。しかし反例も見つかっていないので、恐らく成り立つだろうと肯定的に支持されています。

この予想によれば、素数$p$を用いて $p^2+4$ と表せるような素数は無数に存在することが予想できます。･･･とはいえ、どの$p$で $p^2+4$ が素数になるかについては全く別問題です。ハッキリ言って本問は捨て問です(笑)。

●　　　●　　　●

（２）

一般性を失うことなく $p \leqq q$ と置くことができる。また、$p$、$q$が$1$より大きい公約数をもつとすると $p^q+q^p$ は素数になり得ないので、$p$、$q$は互いに素であることが必要である。

$p=1$ のとき、$$\begin{align}& \ \ \ \ \ p^q+q^p \\ &=q+1 \end{align}$$より、これが素数となるためには$q$が任意の素数より$1$だけ小さい正整数であればよい。

以下、$p \geqq 2$ の場合を考える。

$p=2$ のとき、$$\begin{align}& \ \ \ \ \ p^q+q^p \\ &=2^q+q^2 \end{align}$$となる。ここで$\bmod{3}$を考えると、これが素数となるためには$q$が奇数であり、かつ$3$の倍数であることが必要となる。･･･。

●　　　●　　　●

場合分けが多すぎるのも大概ですが、恐らくこれも未解決問題なので（２）も捨て問です(笑)。$p$、$q$が「自然数」ではなく「素数」であれば話は別なのですが･･･。

※因みに$p$、$q$をともに素数とした場合の問題が2016年の京都大学文理共通第2問に出題されています。本問はこれにインスパイアされた出題と思われます。

というわけで、第1問は全くマジメに解くことができない問題でした(笑)。

 

 第2問

（国際信州学院大学2017年　第２問）

---

さて、何やら難しそうな問題です。これを陰関数化するのは式の形を見ても明らかに絶望的です。これが実際に出題されてしまったら、領域$S(B)$だけを適当に図示しておけば良いでしょう(笑)。

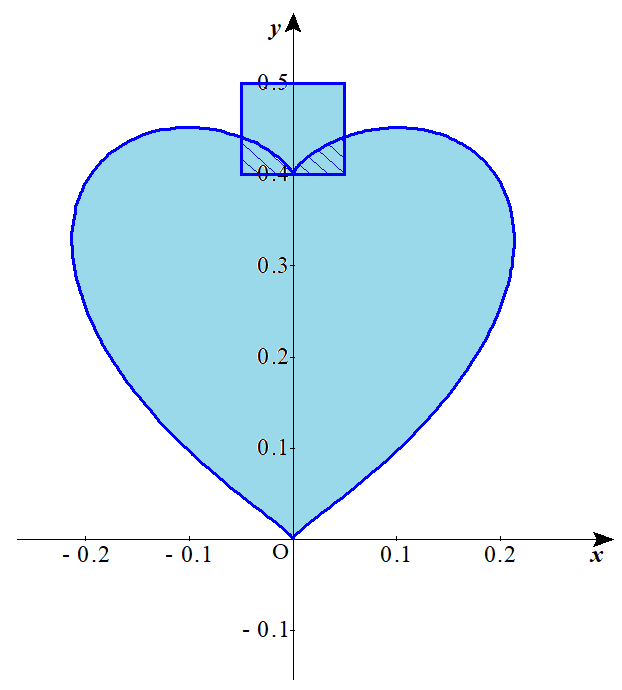
因みに図示すると以下の様になります。図示すべき領域は下図の境界を含む水色部分です。（長野の特産物であるリンゴを象ったシルエット(？)と好意的に解釈できなくもないですが･･･）

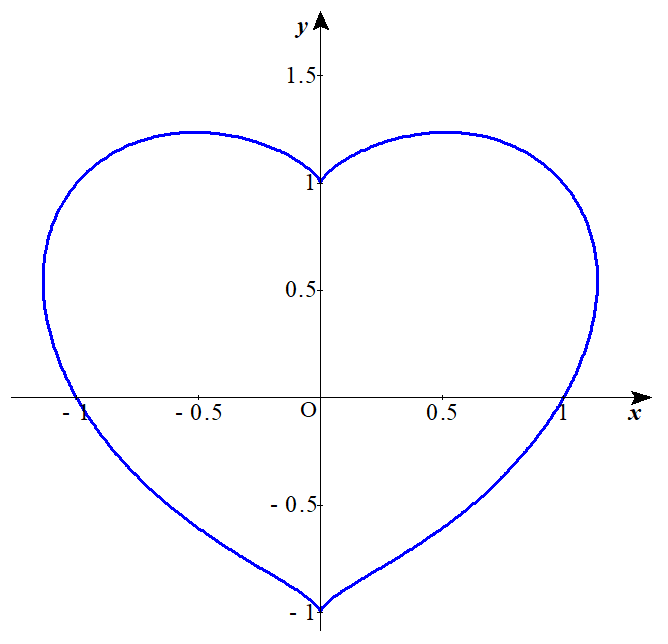
余談ですが、グラフがハート型となる関数は幾つか知られており、$$(x^2+y^2-1)^3 = x^2 y^3$$なんかは式の形がかなりシンプルで良い感じです。グラフは以下のようになります。

 

 第3問

（国際信州学院大学2017年　第３問）

---

このセットの中では最も「典型的な」問題ですね。$\mathrm{K}$は重複していますが、ここでは2枚のカードを$\mathrm{K}_1$、$\mathrm{K}_2$のように区別して考えます。

（１）は両端の$\mathrm{K}$の並べ方と、中央の6枚の並べ方を考えて$$\dfrac{2! \cdot 6!}{8!}=\dfrac{1}{28}$$

（２）は両端の子音のとり方・並べ方と、中央の6枚の並べ方を考えて$$\dfrac{{}_{3}\mathrm{P}_{2} \cdot 6!}{8!}=\dfrac{3}{28}$$

（３）は$\mathrm{K}$のとり方と、先頭の$\mathrm{K}$と末尾の$\mathrm{N}$以外の6枚の並べ方を考えて$$\dfrac{2! \cdot 6!}{8!}=\dfrac{1}{28}$$

（４）は$\mathrm{KK}$を一つの文字として考え、7枚の並べ方、$\mathrm{KK}$内の並べ方を考えて$$\dfrac{2! \cdot 7!}{8!}=\dfrac{1}{4}$$

（５）は（４）の余事象を考えて$$\dfrac{3}{4}$$

●　　　●　　　●

恐らくですが、この設問の流れから察するに、本問は2005年の帝京大(医)の確率の問題がベースになっているのではないかと思われます。今回の問題の中で最も「教育的」だと言えるでしょう。

 

 第4問

（国際信州学院大学2017年　第４問）

---

本セットの問題でも一際目を引くのがこの第4問。なかなか面白い問題設定です。ただ残念ながら $\LaTeX$ ではリンゴ積の記号が出力できないので、ここでは代わりに「$@$」を使うことにします。

（１）は二項演算「リンゴ積」が可換であることの証明問題、（２）は「リンゴ積」が和に対して分配的であることの証明問題となっています。自明と言えば自明･･･かもしれませんが。

（１）は、まず右辺を変形してみます。

$$g @ f = \displaystyle \int^t_0 f(t-s)g(s)ds $$となっているので、$u=t-s$ と変数変換すると、

$s$：$0 \ \to \ t$
$u$：$t \ \to \ 0$

であり、$$\dfrac{d}{ds}u=\dfrac{d}{ds}(t-s)$$ $$\therefore \dfrac{du}{ds}=-1$$ $$\therefore du=-ds$$となるので、$$\begin{align}& \ \ \ \ \ g @ f \\ &= \displaystyle \int^t_0 f(t-s)g(s)ds \\ &=\displaystyle \int^0_t f(u)g(t-u)(-du) \\ &=\displaystyle \int^t_0 f(u)g(t-u)du \\ &=\displaystyle \int^t_0 f(s)g(t-s)ds \end{align}$$（※注：最後の式変形はダミー変数を$u$から$s$に替えただけです）

これより、$$f @ g=g @ f$$が示されます。

続いて（２）ですが、積分の分配性を利用すれば証明するまでもないような気がしますが･･･$$\begin{align}& \ \ \ \ \ f @ (g_1+g_2) \\ &=\displaystyle \int^t_0 f(s) \left\{g_1(t-u)+g_2(t-u)\right\}ds \\ &=\displaystyle \int^t_0 f(s)g_1(t-s)ds+\int^t_0 f(s)g_2(t-s)ds \\ &= f @ g_1 + f @ g_2 \end{align}$$より、従います。

●　　　●　　　●

見慣れない「🍎」が登場していますが、中身自体は簡単な定積分の性質に関する問題でした。三角関数のような周期関数とリンゴ積を融合した問題なども作れそうです。この第4問もどこかの大学の過去問に元ネタがありそうな気がしますね･･･。

---

 

 

---

（2021/09/30追記：本文のスタイルを一部変更）