こんにちは。管理人のpencilです。
行く1月、逃げる2月、去る3月とは言いますが、今年も早1/4が終わろうとしています。『勧酒』という有名な漢詩がありますが、3月と言えば卒業式をはじめ、送別会に追い出しコンパと別れを惜しむ機会が多く、まさに「人生足別離」といった心情になりがちです。4月からは新しい生活を始める方も多いことと思いますが、別れの後にはきっと素敵な出会いが待っていることでしょう!
2018年大学入試総括
さて、今年も大学入学が一段落しましたので、今年の入試問題の概観を勝手に述べていきたいと思います。言うまでもなく、本稿の内容がすべて正しい訳がありませんので、気楽にお付き合い頂ければと思います(笑)。
昨年の大学入試では、主要な大学で出題ミスが相次いだため、どの大学も問題作りにかなり慎重な姿勢を取ったことと思います。ところが今年も出題ミスが発生してしまったようです。京都大学の化学で問題文が不適当として問題2問が削除され、10箇所以上の修正が行われたほか、千葉大の物理(力学)の試験問題において試験終了後に問題の不備が見つかり、1000人以上の受験者全員に加点したという事案がありました。今年は他にも愛知教育大や和歌山大、奈良県立医科大(後期)、金沢医科大、同志社大、立教大など多数の大学で出題ミスがありました。入試問題を作る大学教員の苦労については末尾のコラムに譲るとして、受験生の立場に立ってみると怒り心頭どころの騒ぎではないでしょう。傍観者である私も何だかやるせない気持ちになってしまいます。
今年の入試問題について
今年の入試問題そのものはというと、管理人自身があまり時間が取れずちゃんと見れていなかったというのもありますが、後年に亘って語り継がれる奇問難問の類は出題されていなかったように思います。ほとんどの大学は平常運転ですね。
以下、管理人が気になったポイントを少し挙げていきます。
● ● ●
東大理科数学の難易度はここ数年と比較するとやや回復したかなという印象を受けました。文科の試験に関してはそれほど難しくなっておらず、例年並みくらいでしょうか。
物理や化学に関しては昨年よりやや難化の傾向にあるようですが、全体としては概ね平年並みといったところでしょう。英語では今年の英作文もイラストを基にした問題ではなく、題材としてシェイクスピアの悲劇「ジュリアス・シーザー」の第1幕第2場の台詞が選ばれていました。なお、理科の合格最低点がかなり大きく下がりましたが、これは一体なぜなのでしょうか・・・?また、今年から理科Ⅲ類の面接試験が復活しましたが、効果の程は現時点ではよく分かりません。医学部の面接というのは、ほとんど有って無いようなものですからね・・・。
● ● ●
京大数学は理系の確率の問題(複素平面と確率漸化式の融合題)よりも文系の確率の問題の方が難しかった気がします。京大では確率漸化式が頻出ですから、多くの受験生は対策済みだったと思います。空間図形の良問が文理共通で出題されていたのも興味深いですね。今年の整数問題は目の付け所が良ければ超易問だったことから、来年の整数問題は難化するのではないでしょうか!(笑)
今年の京大英語は英作文のスタイルがかなり変わりました。長文英訳が出題されなかった代わりに、会話文中の空欄に適当な英文を補充するタイプの英作文が出題されており、個人的には2012年の独自リスニング廃止以来のメジャーチェンジに思われました。教育課程はともかく、大学の求める学生像を反映すると言われる入試問題が変わるということは、大学を含め、社会が変わってきているということなのでしょうか。
● ● ●
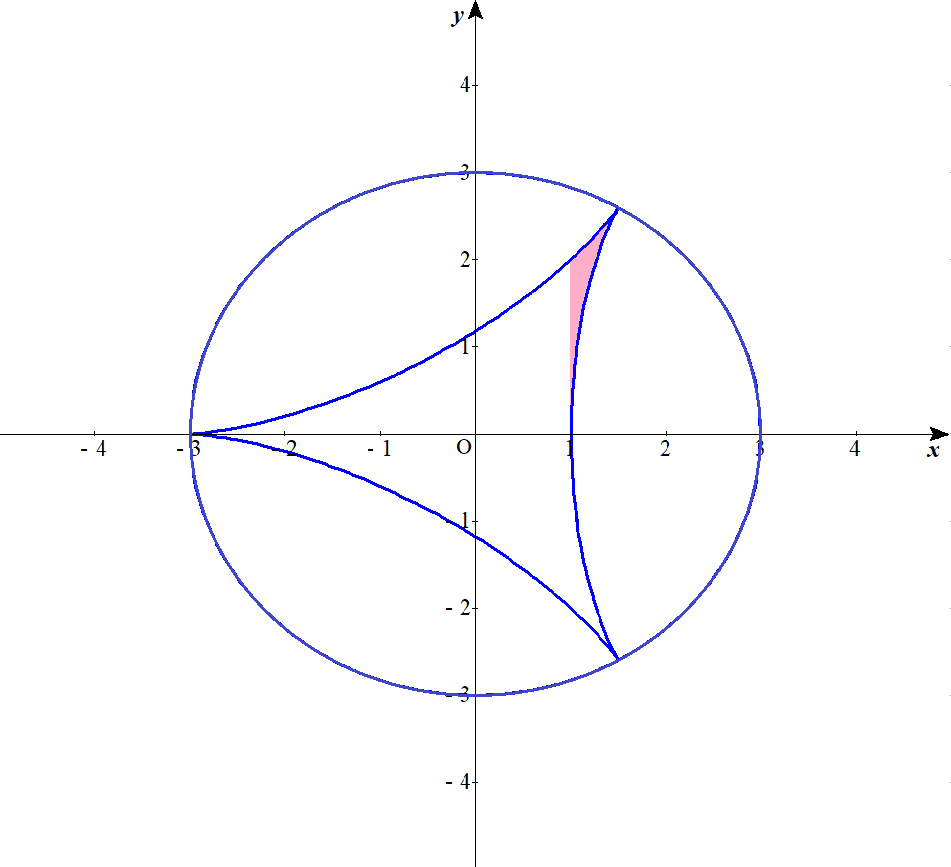
今年の阪大数学は難しかったと思います。中でもハイポサイクロイド(hypocycloid)の問題(理系第3問)や、正八面体の問題(文系第3問/理系第4問)はイメージできないと苦戦を強いられたことでしょう。ハイポサイクロイドは2011年の阪大後期に5頂点のものが出題されていますが、ここまでカバーしていた受験生は少なかったものと思います。今年の理系第3問で題材となったハイポサイクロイドは「三芒形」(デルトイド)と呼ばれます(下図)。四尖点形であるアステロイドが「星芒形」と呼ばれていることは有名でしょう。
因みに、正八面体の問題に関してですが、阪大数学で正八面体を題材とした問題が出題されたのは恐らく初めてのことではないかと思います。過去には東大などで正八面体の断面図の考察が出題されていますので、対策していた受験生がいたかもしれません。これはかなり差の付く問題だったと思います。
なお、今年の阪大物理は力学、電磁気、原子・熱力学というメニューでした(昨年のあの件があったので、やはり波動分野は避けますよね・・・(笑))。それが奏功してか分かりませんが、(縁起でもないですが「今のところは」)今年の阪大では出題ミスは無かったようで何よりです。
● ● ●
各大学について語っているとキリがないので、この辺りで切り上げて、全国的な傾向について見てみます。
出題分野のトレンド
まず第一に、どの大学の試験問題を見ても必ずと言って良いほど、ありとあらゆる大学で複素平面分野からの出題があります。旧課程では行列が数Cの目玉として君臨していましたが現行課程ではきれいさっぱり無くなって、代わりに数Ⅲに複素平面と曲線が入ってきました。もう複素平面を出し惜しみする大学は無くなったと言って良いでしょう。難関大を志すのであれば複素平面分野について十分な対策をしておかなければなりません。
ついこの間話題になった新学習指導要領案では、文系の学生にとってベクトルが必修でなくなる(今度復活する数Cに詰め込まれる)代わりに、文理共通でデータの分析・統計が必修になるとのこと。「文系のカリキュラムからベクトルを消すほど統計が大事なのか・・・?」と、管理人は疑問に思ってしまいます。ベクトルを学ばないと物理の履修が覚束ないというのは少し考えれば分かるはずなのに、なぜベクトルを追いやるようなことをするのでしょうね(まあ現行課程でもベクトルは数B分野なので、初等力学を学ぶ際には(恐らく多くの高校では)未習、という状況に変わりはないのですが・・・)。
また、旧帝大では、これもほぼ必ずと言って良いほど整数問題が出題されています。新学習指導要領案では整数の単元が見かけ上は消滅していますが、数Aにはちゃんと残っていますので、今後も対策はしっかり行っておく必要があります。
その他にもツッコミどころがある新学習指導要領案ですが、高校卒業時点で身に付いている(はずの)数学力としては現行課程のそれと大差ないでしょう。
つまりザックリ言うと、次の新課程でも数学として学ぶ内容はあまり変わらないがデータの分析・統計のウェイトがやや重くなる(あと、ベクトルを学ぶ時期が遅くなる)、というのがこの指導要領案の中身です。今の小学生が高校に進学する頃に実施されるこの新学習指導要領案。大学入試の形も少しずつ変わっていくのかもしれません。
今年の目立った入試問題
以下、個人的に興味を引いた出題を挙げていきます。
-
- 東北大学 理系 第3問でカタラン予想(ミハイレスクの定理)の特殊な場合がが出題される
- 群馬大学 (医) 第3問でやや珍しいタイプのチェビシェフ多項式が出題される
- 京都大学 文系第4問/理系第6問で等面四面体の二等分に関する論証が出題される
これは特に出題という訳ではありませんが、一橋大学の整数問題は第1問に設置されるのが長きに亘って慣例だったのですが、昨年はそれを破って第2問として出題されていました。今年はどうなるのかと思っていましたが、また第1問に戻りましたね。一橋大学前期の数学第1問が整数問題でなかった年は、21世紀に入ってからだと2017年と2004年だけです。因みに90年代では1993年、1991年の2年だけです(それ以前はそもそも整数問題が出題されていなかったりします)。
また、慶應義塾大学 (医) 物理第2問では、単振動における変位の一般式の導出というやや珍しい出題がありました。
コラム:出題ミスについて
昨年の京都大学、大阪大学の入試問題で出題ミスが発生してしまい、合格相当だった当時の受験生が約1年経ったこの時期になって大学への入学を案内されるという騒動があったのは記憶に新しいことと思います。昨年のコラムでは大学入試問題を作る大変さについてお話しましたが、今回も大学教員の苦労話が中心になります・・・。
本来、大学教員の仕事は研究なのであって、入試問題の作成ではありません。もちろん質の良い試験問題を作って、優秀な学生を集めるというのは大学にとって重要なことではありますが、昨今の大学教員の忙しさを考えればそれも悪い冗談に聞こえます。アカデミックの世界は競争が熾烈であり、有能なスタッフになればなるほど色々な作業に確保できる時間は乏しくなります。国内外にアンテナを張りつつ、研究を進めては論文を執筆し、寝ずに実験をしたり、大学の講義を行ったり、海外へ出張に行ったり、研究費確保のためにあちこち奔走したりと、入試問題の作成に関わっている暇など無いのです。特に実験系の研究室ですと、ところによってはそれこそブラック企業顔負けの働きぶりで研究に取り組んでいる研究室も多数存在します(※勿論、上記の話は研究室にも依りますし、これは主に理系分野の話であるということは断っておきます)。
そんな中で(一応)秘密裏に入試問題を作成するというのは、数ある大学の事務作業の中でもトップクラスに大変なことなのです。問題作成に加えて、合格発表に間に合うように採点もしなければならないのですから、どうしても貴重な研究時間が削られてしまいます。文科省によって次々と打ち出される大学教員数の削減や教育改革などにより、学部長や学生部長などを務めようものなら膨大な事務作業も相まって多忙を極めること必至です。そんな事情がありながら入試問題を作る大学教員の方々は感謝されこそすれ、非難される謂れなど無い・・・と言っても差し支えないでしょう。
様々なタスクを抱えながらの入試問題の作成ですから、たまに注意が行き届かないケースが出てきてしまいます。入試問題というのは基本的に数人で手分けして作成されるものですが、会議等で差戻しになれば良いものの、出題ミスに誰も気付かないままうっかりパスしてしまうこともあるのでしょう。パスした後の入試問題を、作問者以外の人間がわざわざ自分の時間を割いてまで点検しないでしょうから、結局試験終了後まで出題ミスが判明しないという事態に陥ってしまいます。
また、大学教員は受験生の想像以上に高校範囲の内容について知りません(というより、覚えていません)。これは高校生からすると信じられないことかもしれませんが、大学では非常に専門性の高い研究を行っているため、広く浅くが基本である高校の内容などはきれいさっぱり忘れ去られています。これは筆者が大学初年度に目の当たりにした事実なのですが、たとえ数学者であっても人によっては $\sin x$ の微分を定義から導く方法すら忘れ去っています(笑)。普段から高度に抽象的な研究や、あまりに専門的な研究をしている方々にとって、入試問題の作成というのは、仮に時間がたっぷり有ったとしても、そもそもかなり骨の折れる作業なのです。
勿論、入試問題がどのように作られるのかについては各大学によって変わってくるでしょうから一概には何とも言えませんが、試験の前(というよりは問題冊子を印刷する前)に試験問題の草案に対してミスが無いか点検し、指摘する立場の人間がいないことが大きな問題だと考えられます。
昨年の当欄で紹介した「入試過去問題活用宣言」は、問題作成の負担を軽減すると同時に、そうした出題ミスのリスクを軽減するという役割も持っていると言えます。中には予備校に試験問題の作成を委託している大学があるとかないとかいう怪しい噂もあったりしますが、管理人個人としては、せめて大学入試の問題は大学が自前で作るのが良いと考えています。ただ、大学教員も人間ですから、時にはミスもします。入試問題を作成する専門チームを作ったり、出来上がった問題を点検するアドバイザーを雇ったところで根本的な問題解決にはなりませんが、こうした対策が現実的に提案できる(資金さえ確保できれば)最善の方法ではないかと思います。
まあ、そのうちAI(人工知能)が何でもかんでも引き受けてくれるようになるんじゃないだろうか!(笑)
● ● ●
出題ミス各論(笑)
・・・というかなり適当な終わり方をしてしまうのも宜しくないですので、出題ミスそのものについても少し考察しておきましょう。出題ミスには少なくとも次の数種類のパターンがあります。
①日本語の誤り
②条件の不足
③条件の誤り
④範囲外からの出題
⑤その他???
それぞれについて受験者の立場で考えてみましょう。
問題冊子が配られ、「解答始め」の合図の後、試験場の受験生はまず各問題を見渡します。その中で最も早く気付ける出題ミスが「①日本語の誤り」でしょう。ちゃんと問題文を読めば受験生たる者、誤字脱字くらいは容易に判別できます。このタイプのミスについては出題サイドも何重にもチェックしているので、まずお目にかかることはありません。
次に巡り合う可能性の高いミスは「②条件の不足」でしょう。これは主に理系教科で観測されます。出題サイドは作問の過程で複数通りの模範解答を予め用意しておくので、その作業の過程で条件の不足に気付くことはできるはずです。なので、もしこのような出題ミスがあれば大学側の初歩的な確認不足としか言いようがありません。
このタイプの出題ミスに遭遇してしまったときは、数学の場合だと解が不定となったり変数が残ったりしますので、何となく(?)諦めることができますが、悲惨なのが理科科目の場合。それ以降の設問の解答に支障が出る場合は最悪です。パニックになってしまい実力を発揮できずに試験終了、という受験生も出てきてしまうでしょう。
更に厄介なのが「③条件の誤り」だと思います。これも主に理系教科で観測されます。受験生はまさか問題設定そのものがおかしいなどとは考えませんから、解答不能な問題に余計な時間を取られてしまい、場合によっては試験全体のコンディションに影響を及ぼしてしまう可能性すら考えられます。計算問題であれば自分の計算ミスを疑うのが普通ですから、時間の浪費となってしまう危険性がかなり大きくなります。しかし、問題が解答不能になるのはまだマシな方で、最も罪深いのは、何となく解答が継続可能な場合です。
例えば前問の数値を引き継ぐタイプの問題の場合、数値が丸っきりおかしいと注意深い受験生なら問題のミスに気付くことができるかもしれませんが、誤った条件の下で導き出された数値が後の設問でもそれっぽく使用できてしまうと大変です。このようなケースへの対処は大学側の判断に依るところが大きいですが、仮に全員加点となった場合、その問題を時間を掛けてせっかく解いた受験生は全く報われません。大損です。
しかし実際の出題ミスはほとんどが②や③のタイプであり、今年も多数の大学で出題ミスが相次ぎ、追加合格を出すなどの措置が取られました。やはり出題ミスは無くなりませんね。
なお、それ以外のタイプの出題ミスですが、「④範囲外からの出題」というのは出題「ミス」として良いか微妙なところです。社会科科目の問題で極めてマニアックな出題をする大学もあることですし、どこまでを入試問題の許容範囲とするのかは各大学の裁量に委ねられている部分が大です。解けない問題は潔く捨てるというのも受験における立派な戦略の一つと言えるでしょう。
・・・ところで、⑤の「その他???」というのは何なんでしょう(笑)?
こうした議論の際にしばしば引き合いに出されるのが次の問題です。
次の方程式で表される $xy$ 平面上の$3$直線 $l_1$、$l_2$、$l_3$ を考える。
$l_1:x+y-1=0$ $l_2:x-y+1=0$ $l_3:x+k=0$ (ただし$k$は$0$でない定数)
このとき次の各問に答えよ。
(1)1次変換 $f$ により $l_1$ が $l_2$ に、$l_2$ が $l_3$ にうつされるとき、この1次変換 $f$ を表す行列 $M$ を $k$ を用いて表せ。
(2)$3$直線 $l_1$、$l_2$、$l_3$ でつくられる$3$角形の重心が、(1)の1次変換 $f$ により原点にうつされるとき、$k$ の値を求めよ。
(神戸大学1982年共通 第1問)
実際に解いてみればお分かりになると思いますが、この問題、何と(2)の$k$は「存在しない」が正解なのです。出題した当の神戸大は「世の中のすべての問題に解があるわけではない」などと開き直っていたようで、まあ確かにその通りではあるのですが、大学受験でそれをやるか(笑)?という感じですね・・・。これを単なる不親切な問題だと思うか、問題設定の誤りだと思うかは皆さんにお任せしますが、世の中にはこうしたひねくれた問題も何かの加減で出題され得るのだということを頭の片隅に置いておくと良いでしょう。解ける問題から解答するという基本を徹底し、もしもの時でも動じない精神力が非常に大切です!
全体を通して
国立情報学研究所(NII)が「ロボットは東大に入れるか」というプロジェクトの下で開発した「東ロボ君」は、自然言語の処理に難があるということで東大進学を断念しました。これには色々な理由があるそうですが、一番の理由は読解力や批判的な思考力を身に付けられなかったからだそうです。このプロジェクトの中心メンバーであるNIIの新井紀子教授の調査結果によれば、中高生の1/3は読解力や批判的な思考力が十分には身に付いていないとのことです。人間にとって苦手なことはAIも苦手、ということであれば、AIが入試問題を作れるようになるにはまだまだ時間が掛かりそうです。
因みに、管理人が専門にしている分野はAI産業とのタイアップが割と期待されているのですが、人工知能やディープラーニングといった分野はどうも勉強しなければならないことが多すぎますね・・・。道のりは平坦ではなさそうです。

“2018年大学入試総括(主に数学)” への2件の返信