「テイラー展開」の分かりやすい解説

この記事では「テイラー展開」という数学的操作について例を交えて分かりやすく解説します。

---

 

 微分すれば関数が求められる

$y=ax^2+bx+c$ という関数は皆さんも馴染み深い「放物線」の関数ですね。ある放物線のグラフが与えられたときに、その放物線の方程式を決定せよ、と言われたらどうすればよいでしょうか。

多くの人は、放物線が通る3つの点の座標を方程式に代入して得られる連立方程式を解くことで各係数を決定すると思います。未知数が3個なので、3本の方程式を連立する必要がある、というのは何となく理解できますよね。

では、放物線上のある1点の情報が3つあれば、原理的には全ての係数を決めることができるのではないでしょうか？

---

関数 $y=ax^2+bx+c$ を$x$について微分すると、$$y^{\prime}=2ax+b$$という第1次導関数が得られます。これをさらに微分すると、$$y^{\prime\prime}=2a$$という第2次導関数が得られます。

つまり、ある１つの座標における「値$y$」と「傾き$y^{\prime}$」（1次微分）と「傾きの傾き$y^{\prime\prime}$」（2次微分）が分かれば、どんな放物線の方程式でも求められるのです。

これは

「3点$(0,2)$、$(1,1)$、$(3,5)$を通る放物線の方程式を求めなさい」

という問題の答えと、

「曲線上の点$(0,2)$における1次微分が$-2$、2次微分が$2$である放物線の方程式を求めなさい」

という問題の答えが一致することを意味しており、実際にどちらも答えは$$y=x^2-2x+2$$となります。

---

このことは3次関数でも4次関数でも同じです。3次関数であれば、ある点での1～3階微分までの値が分かれば方程式が決定できますし、4次関数なら1～4階微分までの値が分かればOKです。

一般の$n$次関数についても全く同じことが言えます。つまり、その関数が通るある1点における「値$y$」と「1次微分$y^{(1)}$」～「$n$次微分$y^{(n)}$」が分かってしまえば、（計算は大変ですが）原理的にはどんな関数の方程式でも決定することができるのです。

 

 関数を「展開」するということ

$n$次関数というのは普通「整式」です。整式とは根号などを含まない多項式のことです。$n$次関数はどんどん微分すれば幾らでも係数が求められますが、それ以外の関数ではどうでしょうか？

例えば三角関数の代表選手 $y=\sin x$ なんかを観察してみるのが良いかもしれません。三角関数は整式ではないので、係数(？)がよく分かりません。そこで、「$\sin x$ が$$(*) \quad a_{0}+a_{1}x+a_{2}x^2+\cdots+a_{n}x^n+\cdots$$のように整式で表せる」という大胆な仮定を置いてみます。取り敢えずこれが数学的に正しいかどうかは一旦脇に置いておき、このように表せるものとして話を進めます。

正弦関数 $\sin x$ を微分すると $\cos x$ になり、さらに微分すると $-\sin x$、さらに微分すると $-\cos x$、もう一度微分すると $\sin x$ に戻ってくるという性質がありましたね。

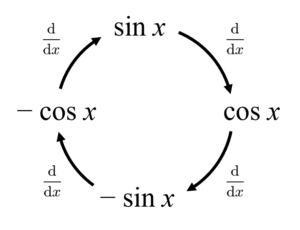
計算を簡単にするために $f(x)=\sin x$ を何度も微分して $x=0$ を代入していくことにします。なぜ $x=0$ を代入するのかというと、$(*)$式の$n$次導関数に $x=0$ を代入すれば$n$次以上の高次の項は全てゼロになるので、下図のように係数$a_n$が一つずつ求められるからです。

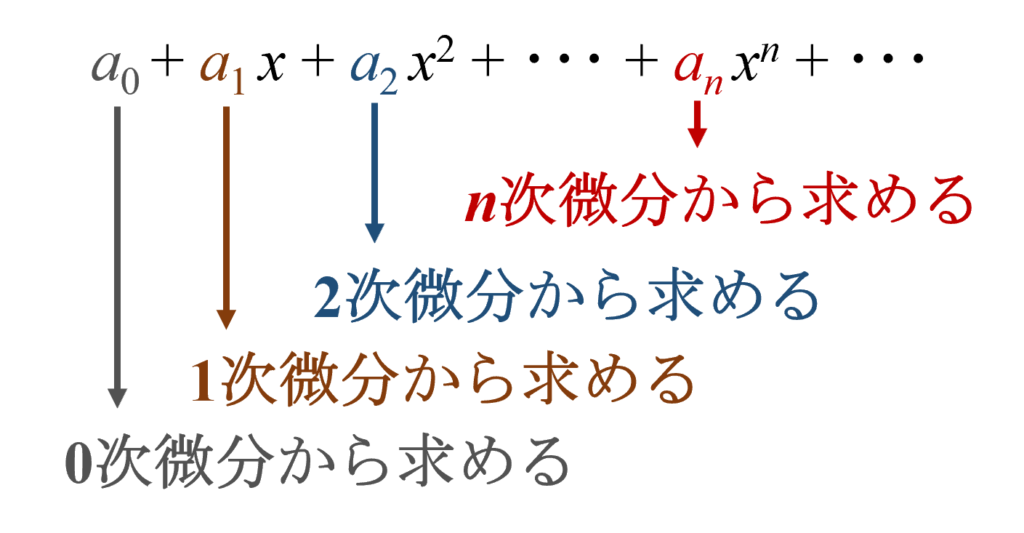
※計算の際は、$n$次の項を$0$次になるまで微分すると係数が$n! a_n$になることに注意。

---

まず、$f(0)=\sin 0 = 0$ なので、$$a_{0}=0$$と決まります。$\sin x$の一次微分は $\cos x$ ですから、$f^{(1)}(0)=\cos 0 =1$ より、$$a_{1}=1$$と決まります。これで今のところ$$\sin x \fallingdotseq 0+x$$という表式が得られています。もっと続けていくと、$$a_{2}=0$$ $$a_{3}=-\dfrac{1}{6}$$ $$a_{4}=0$$ $$a_{5}=\dfrac{1}{120}$$ $$a_{6}=0$$ $$a_{7}=-\dfrac{1}{5040}$$ $$\vdots$$となるので、$$\sin x \fallingdotseq x-\dfrac{x^{3}}{6}+\dfrac{x^{5}}{120}-\dfrac{x^{7}}{5040}+\cdots$$と表せるようです。グラフは次のようになります。項が増えるごとに$\sin x$に近付いているのが分かりますね。

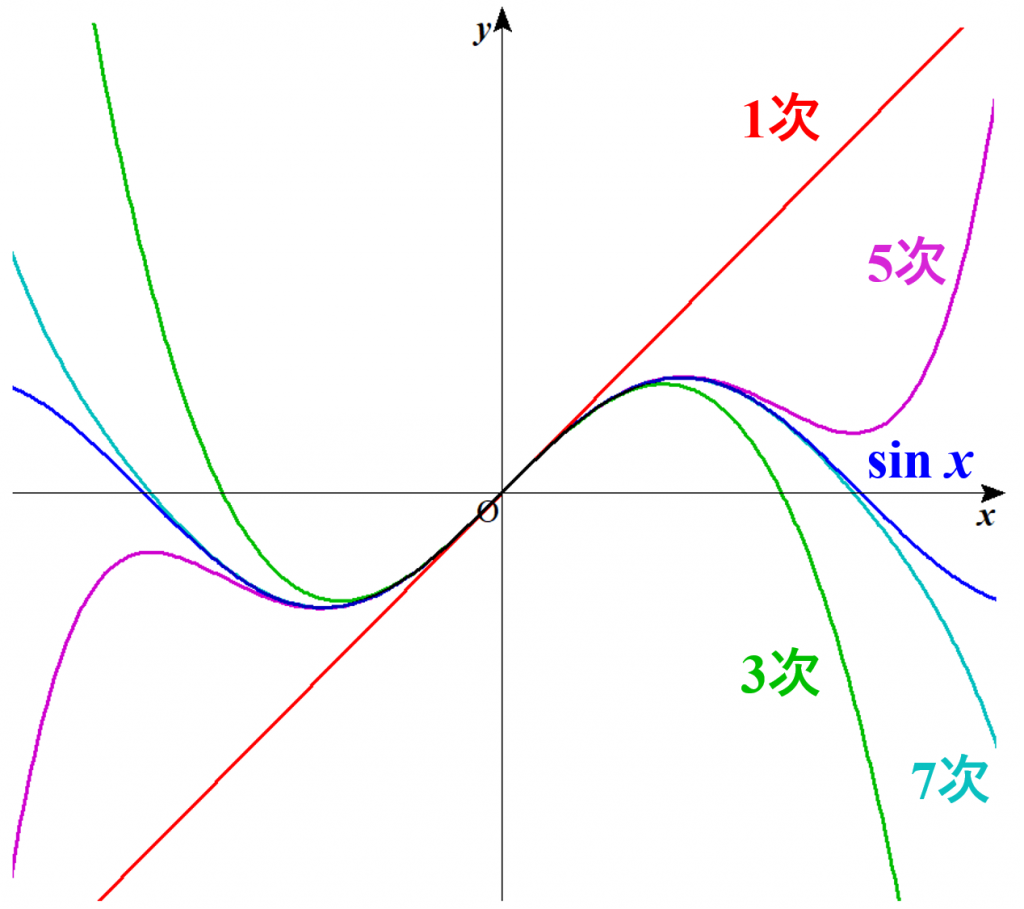
しかし$\sin x$は何回でも（無限回）微分可能なので、項の数は幾らでも増えていくはずです。つまり、$\sin x$は上記のように表示できることにはできますが、いつまでも終わりが見つからない関数だということになります。

※このような関数は「超越関数」と呼ばれます。三角関数のほか、指数関数や対数関数などは代表的な超越関数です。

そして実際に、$\sin x$は無限個の冪（べき）乗項の和（級数）として表すことが可能です。このように関数を級数で表示することは「級数展開」と呼ばれます。

※文脈上の意味が明確なときは単に「展開」と呼ぶこともあります。

 

「テイラーの定理」について

関数の級数展開に関して「テイラーの定理」という重要な定理が知られています。

関数をこのように表示することを「テイラー展開」と呼びます。上式は有限個の項で打ち切っているため、正確には $n-1$ 次までの「有限テイラー展開」と呼ばれます。テイラーの定理は、ロルの定理を既知とすれば（少し上手いアイデアが必要ですが）高校数学の範囲でも一応証明可能です。

先ほどの例では $f(x)=\sin x$ としていましたが、この関数$f(x)$というのは閉区間$[a,b]$内で$n$回微分可能であれば何でもOKです。微分可能な関数であれば基本的には例外なくテイラー展開が可能です。

末尾の項$f^{(n)}(c)\dfrac{(b-a)^{n}}{n !}$は剰余項と呼ばれるものです。$n$次以上の言わば「余った」項を末尾の項まとめて押し込めているので、この名が付いています。$n$が十分大きければ剰余項が十分小さくなって無視できる（ゼロと見なせる）ので、関数$f(x)$を多項式で近似することができます。これにより複雑な関数の代わりに多項式を計算するだけでよくなるので、関数の取り扱いが簡単になります。

※一般に、$\sin x$ などの超越関数は計算が困難です（例えば、$\sin 33^{\circ}$などの値を求めようと思っても解析的に求めるのは難しいですよね？）。そこで、十分$n$を大きくとったテイラー展開を用いて近似的に計算するといったことができます。文献によっては「関数電卓の$\sin x$などの計算にはテイラー展開を利用している」と説明しているものもありますが、実際には多くの場合、テイラー展開による級数ではなくCORDICアルゴリズムというものを利用して三角関数の値が計算されています。

※「有限テイラー展開」の表式は$$\displaystyle f(x)=\sum_{k=0}^{n-1} \frac{f^{(k)}(a)}{k !}(x-a)^{k}+R_{n}$$となります。ここで $R_{n}=\dfrac{f^{(n)}(c)}{n!}(x-a)^{n}$ は剰余項であり、仮に$f^{(n)}(c)$が$x$の値に依存する関数だとしてもテイラー展開の定義から $\displaystyle \lim_{n \to \infty} R_{n}=0$ を満たすので、テイラー級数は$$f(x)=\displaystyle \sum_{k=0}^{\infty} f^{(k)}(a) \dfrac{(x-a)^{k}}{k !}$$とシンプルに書き表すことができます。

「テイラーの定理」の式において $f(x)=\sin x$ とし、$a$に$0$を代入して $n \to \infty$ とすれば、$$f(b)=b-\dfrac{b^{3}}{3!}+\dfrac{b^{5}}{5!}-\dfrac{b^{7}}{7!}+\cdots$$となるので、先ほどの$\sin x$の級数展開に $x=b$ を代入したものに一致しています。

---

テイラーの定理について、もう少し掘り下げてみます。

$n=1$ のとき、有限テイラー展開の表式は$$f(a)+f^{\prime}(c)(x-a)$$となりますが、これは区間$[a,x]$に関する「平均値の定理」そのものです。この式は点 $x=a$ のまわりで1次近似した関数を与えており、点 $(a,f(a))$ を通る直線で元の関数$f(x)$を近似したものに相当します。

$n=2$ のときは$$f(a)+f^{\prime}(a)(x-a)+f^{\prime \prime}(c) \frac{(x-a)^{2}}{2 !}$$という式になります。これは点 $x=a$ のまわりで2次近似した多項式、すなわち点 $(a,f(a))$ を通る放物線で元の関数$f(x)$を近似したものになっています。

平均値の定理は「ある1次関数の存在」を主張するものなので、”2次の平均値の定理” は言ってみれば「ある2次関数の存在」を主張するものと言えます。”$n$次の平均値の定理” がテイラーの定理に対応すると考えれば、よく「テイラーの定理は平均値の定理の一般化である」と言われるのも何となく納得できるのではないでしょうか。これは言い換えると「平均値の定理はテイラーの定理の特殊な場合（$n=1$ の場合）である」ということになります。面白いですね。

---

それから余談ですが、テイラー展開以外にも級数展開の考え方を拡張した関数の表現方法が幾つか知られています。いずれも大学数学や理工学の専門課程で教わる内容です。

テイラー展開を負の冪まで拡張した「ローラン展開」はその一つです。ローラン展開は複素関数の展開に用いられており、複素関数分野で扱う「留数」というものと関係していて複素積分などで利用されます。

また、テイラー展開では関数を冪乗項の級数で表示しますが、三角関数の級数でも似たようなことができるのではないか、という発想で「フーリエ展開」というものが考案されました。フーリエ展開を拡張した「フーリエ変換」はもともと熱力学の問題を解決するために導入されたものですが、電磁気学や音響学、量子力学、経済学など様々な分野で応用されている重要な手法です。

※イギリスの数学者ブルック・テイラー（Sir Brook Taylor, 1685年～1731年）によって「テイラー展開」が提案されたのが1712年、「ローラン展開」がフランスの数学者ピエール・アルフォンス・ローラン（Pierre Alphonse Laurent、1813年～1854年）によって世間に公表されたのが1843年、「フーリエ展開」がフランスの数学者ジョゼフ・フーリエ（Jean Baptiste Joseph Fourier, Baron de、1768年～1830年）によって世間に公表されたのは1807年のことです。

---