「鉄塔の間隔は何ｍ？」～Amazon入社試験より

Amazonの入社試験に出題された問題とその改題についての話題です。

 

 鉄塔の間隔は何ｍ？

早速、問題に入りましょう。

下の図のように、高さ 50 m の鉄塔に全長 80 mのケーブルが渡されています。ケーブルの最下点は地上から10メートルの位置にありました。このとき、鉄塔の間隔は何ｍになるでしょうか？

ただし計算を簡単にするため、ケーブルは鉄塔の先端（高さ 50 m の位置）から吊るされているものとして考えて下さい。

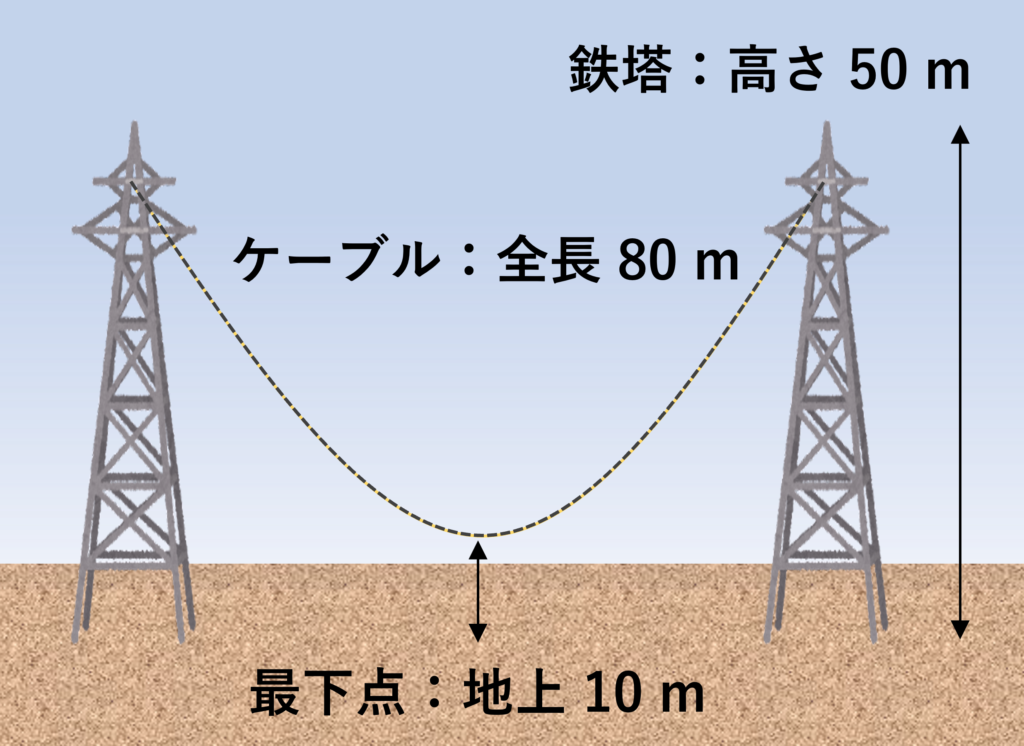
これが今回紹介する問題の概要です（ただし管理人が設定を少しアレンジしています）。こんな問題が実際に出題されたかどうかは定かではありませんが、世間ではAmazonの入社試験問題として伝えられています。

まずは少し考えてみてください。

---

 

 

　♪ ♪
🐓🐤🐤🐤…

 

 

 

 答え合わせ

さて、どうでしょうか？

変な答えになっていれば多分正解です(笑)

---

ケーブルの長さは 80 m なのでその半分は 40 m です。高さ 50 m の鉄塔の先端から 40 m 分のケーブルを吊り下げると地上から 10 m の高さに到達します。つまりこの状態で既に最下点に達した状態になっているのです。

･･･ということは、図の条件を満たすような鉄塔の間隔は 0 m と分かります。「一流企業」にありがち(？)な引っ掛け入社問題というオチでした。既にご存知の方も多かったかもしれませんね。

解答に際して「曲線の長さってどうやって求めるんだっけ？」とか「これって放物線だよね？」とか考えた方はいませんか？

三平方の定理や弧長積分を持ち出すまでもなく、単純に長さを考えれば良いだけの問題なのでした。問題文を一読して難しい数学の問題だと思った方は、数学をやりすぎて(？)アタマが凝り固まってしまっているかもしれません。

それから、ロープなどを吊り下げたときに現れる曲線には「懸垂線」という名前がついています。見た目がなんとなく似ているので時々間違えてしまう人がいるのですが、この曲線は放物線ではありません。

 

 数学の問題にする

ケーブルの長さが 80 m だと吊り下げるには短すぎるようです。そこで例えば、ケーブルの長さが2倍の 160 m の場合、鉄塔の間隔は何mになるでしょうか？

ここでやっと数学の出番です。

---

陽関数（$y=f(x)$ の形で表される関数のこと）の弧の長さは次の公式で求めることができます。

※公式について詳しくは「【曲線の長さの公式】放物線の長さを求めてみよう」のページを参照して下さい。

「懸垂線」は「カテナリー曲線」とも呼ばれ、$$y=\dfrac{a}{2}\left(e^{\frac{x}{a}}+e^{-\frac{x}{a}}\right)$$という一般式で与えられることが知られています。カテナリー曲線の導関数は $y’=\dfrac{1}{2}\left(e^{\frac{x}{a}}-e^{-\frac{x}{a}}\right)$ となるので、$$\begin{aligned} 1+\{f'(x)\}^2&=1+\left(\dfrac{e^{\frac{x}{a}}-e^{-\frac{x}{a}}}{2}\right)^2 \\ &=1+\dfrac{1}{4}\left(e^{\frac{2x}{a}}-2+e^{-\frac{2x}{a}}\right) \\ &=\dfrac{1}{4}\left(e^{\frac{2x}{a}}+2+e^{-\frac{2x}{a}}\right) \\ &=\left(\dfrac{e^{\frac{x}{a}}+e^{-\frac{x}{a}}}{2}\right)^2 \end{aligned}$$より、$x=0$ の点から $x=b$（$b>0$）の点までの弧長$L$は$$\begin{aligned} L&=\int_{0}^{b}\sqrt{1+\{f'(x)\}^2}\,dx \\ &=\int_{0}^{b} \dfrac{e^{\frac{x}{a}}+e^{-\frac{x}{a}}}{2}\,dx \\ &=\left[{\dfrac{a(e^{\frac{x}{a}}-e^{-\frac{x}{a}})}{2}}\right]_{0}^{b} \\ &=\dfrac{a(e^{\frac{b}{a}}-e^{-\frac{b}{a}})}{2} \end{aligned}$$で与えられます。このように弧長公式との相性が良いことから、意外と頻繁に大学入試で出題されている関数でもあります。

※カテナリー曲線を題材とする入試過去問は「カテナリー曲線に関する問題」のページにまとめています。興味がある方は覗いてみて下さい。

---

以上のことを既知とすると、ケーブルの長さと鉄塔の高さから二つの方程式を得ることができます。ここで、解答すべき問題のシチュエーションを図に起こしてみます。

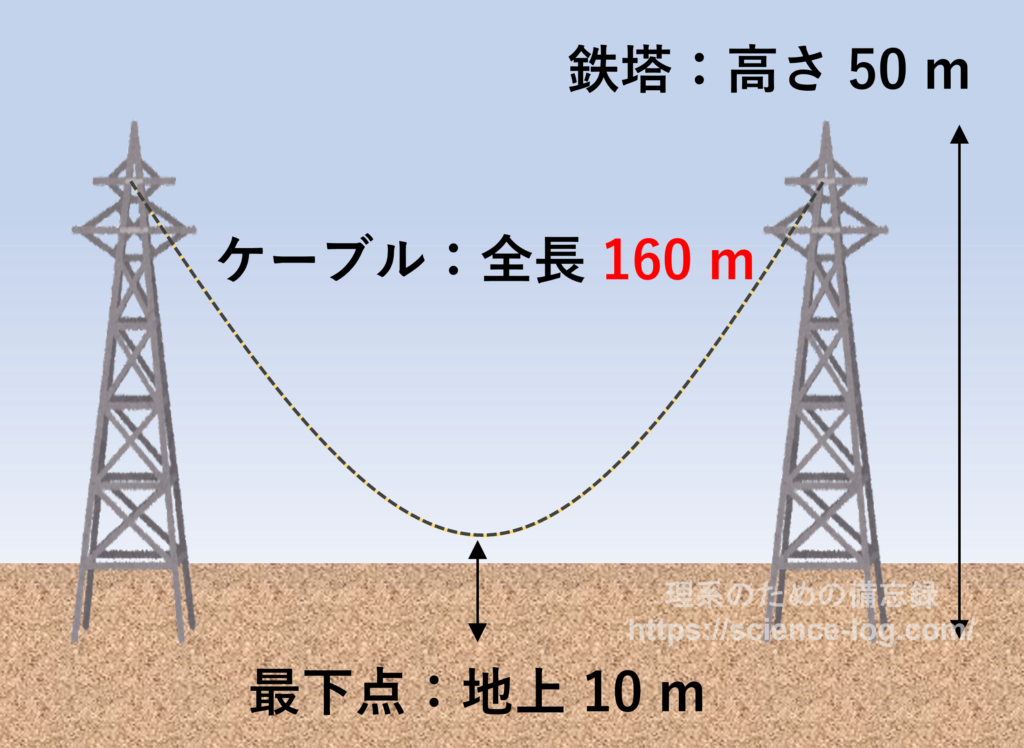
まず、ケーブルが描く曲線の方程式は最下点を $x=0$ とすると、懸垂線の一般式を高さ方向に$h$だけ平行移動したものと考えて$$f(x)=\dfrac{a}{2}\left(e^{\frac{x}{a}}+e^{-\frac{x}{a}}\right)+h$$という式で表せるはずです。これは一般式に定数項$h$を加えただけなので曲線の弧長公式がそのまま使えます（不安な人は$f(x)$の導関数を調べてみて下さい）。

２つの鉄塔の間隔を $2b$ メートルとしましょう。このときケーブルの高さ方向の差分から$$f(b)-f(0)=40$$が成り立ちます。また、ケーブルの半分の長さについて$$\int_{0}^{b}\sqrt{1+\{f'(x)\}^2}\,dx=80$$が成り立ちます。以上から、$$\left\{\begin{array}{l}
40=\dfrac{a}{2}\left(e^{\frac{b}{a}}+e^{-\frac{b}{a}}\right)-a \quad \cdots ① \\
80=\dfrac{a}{2}\left(e^{\frac{b}{a}}-e^{-\frac{b}{a}}\right) \quad \cdots ②
\end{array}\right.$$という連立方程式を得ます。$②+①$、$②-①$ より$$\left\{\begin{array}{l}
120=a e^{\frac{b}{a}}-a \quad \cdots ③ \\
40=a-a e^{-\frac{b}{a}} \quad \cdots ④
\end{array}\right.$$となり、$③ \div ④$ より、$$3=\frac{e^{\frac{b}{a}}-1}{1-e^{-\frac{b}{a}}}$$ $$\therefore 3-\frac{3}{e^{\frac{b}{a}}}=e^{\frac{b}{a}}-1$$ $$\therefore e^{\frac{2b}{a}}-4e^{\frac{b}{a}}+3=0$$ $$\therefore (e^{\frac{b}{a}}-3)(e^{\frac{b}{a}}-1)=0$$ $$\therefore e^{\frac{b}{a}}=1 \text{ または } 3$$と求められます。

ここで、$e^{\frac{b}{a}}=1$ となるのは$a$が無限大か $b=0$ の場合に限られるので問題の条件に合いません。したがって $e^{\frac{b}{a}}=3$ が解となることが分かります。これを$③$に代入して$a$について解くと $a=60$ を得るので、$b=60 \log 3$ と求められます。

また、$x=0$ の点における条件として $a+h=10$ があるので $h=-50$ となり、題意を満たすケーブルの曲線は$$f(x)=\color{red}{30\left(e^{\frac{x}{60}}+e^{-\frac{x}{60}}\right)-50}$$という式で表せることが分かります。実際、この曲線 $y=f(x)$ は $x=60 \log 3$ で $y=50$ をとります。

$60 \log 3 = 65.91673…$ なので、鉄塔の間隔はこれを2倍して大体 132 m 程度と見積もられます。これは立派な数学の問題と言えますね！

---