【数学夏祭り】第7’問（関数方程式）について【2020年夏】

先週まで2週間にわたって開催された「数学夏祭り」第7問の代替問題（第7’問）について解説･考察してみました。

第1問についてはこちらから→【数学夏祭り】第一問（整数問題）の解説【2020年夏】

第4問についてはこちらから→【数学夏祭り】第4問（確率）の面白さについて【2020年夏】

---

【数学夏祭り】第７´問

---

（数学夏祭り(2020) 第7´問）

 考え方

設定が抽象的であり難易度は高めですが、ステップを追って考えれば実は単純な問題です。

1番目の条件は定義域（$x$の範囲）が実数全体の集合$\mathbb{R}$のうち非負であるような部分集合であること、2番目の条件は$f(x)$の値域が実数全体の集合$\mathbb{R}$のうち非負であることを意味しています。

さらに3番目の条件より、$f(x)$は上記の範囲で逆関数を持つようです。今回与えられている主な式は$$f(x)=\left[f^{-1}\left(\sqrt{f(x)}\right)\right]+\sqrt{⟨x⟩}\cdots (\ast )$$というもので、ここから出発して考えていきます。

$y=f(x)$ と置くと $x=f^{-1}(y)$ となるので、$(\ast )$より$$y=\left[f^{-1}\left(\sqrt{y}\right)\right]+\sqrt{⟨f^{-1}(y)⟩}$$となります。

ここで $y=7.9(>0)$ を代入してみると、$$7.9=\left[f^{-1}\left(\sqrt{7.9}\right)\right]+\sqrt{⟨f^{-1}(7.9)⟩}$$ $$7.9=\left[f^{-1}\left(\sqrt{7.9}\right)\right]+\sqrt{⟨K⟩}$$となります。いま、$\left[f^{-1}\left(\sqrt{7.9}\right)\right]$は整数であり、$⟨x⟩$ の定義より $0\leqq ⟨K⟩<1$ が成り立つから明らかに$$0\leqq \sqrt{\phantom{(}⟨K⟩}<1$$となるので、$7.9$の整数部分が$\left[f^{-1}\left(\sqrt{7.9}\right)\right]$であり、$7.9$の小数部分が$\sqrt{⟨K⟩}$となることが分かります。

したがって$$\sqrt{⟨K⟩}=0.9$$ $$\therefore ⟨K⟩=0.81$$を得ます。

次に $y={7.9}^2(>0)$ を代入してみると、$${7.9}^2=\left[f^{-1}\left(7.9\right)\right]+\sqrt{⟨f^{-1}({7.9}^2)⟩}$$ $$62.41=\left[K\right]+\sqrt{⟨f^{-1}({7.9}^2)⟩}$$となります。いま、$[K]$は整数であり、$⟨x⟩$ の定義より $0\leqq ⟨f^{-1}({7.9}^2)⟩<1$ が成り立つから明らかに$$0\leqq \sqrt{⟨f^{-1}({7.9}^2)⟩}<1$$となるので、$62.41$の整数部分が$[K]$であり、$62.41$の小数部分が$\sqrt{⟨f^{-1}({7.9}^2)⟩}$となることが分かります。

よって$$[K]=62$$が得られます。

以上より、$$\begin{array}{rl}{f}^{-1}\left(\sqrt{7.9}\right)& =K\\ & =[K]+⟨K⟩\\ & =62+0.81\\ & =62.81\end{array}$$と求められます。

 

 逆関数$f^{-1}(x)$のグラフ

上記の方法はオーソドックスなものだと思いますが、これを応用すれば一般の非負実数$x$についても逆関数$f^{-1}(x)$をあらわに与えることができます。

$$f(x)=\left[f^{-1}\left(\sqrt{f(x)}\right)\right]+\sqrt{⟨x⟩}\cdots (\ast )$$という式をもう少し詳しく見ていきましょう。

先ほどの議論と全く同様に$\sqrt{⟨x⟩}$は$1$未満であることから、$(\ast )$より$f(x)$の整数部分が$\left[f^{-1}\left(\sqrt{f(x)}\right)\right]$に一致すること、つまり、$$[f(x)]=\left[f^{-1}\left(\sqrt{f(x)}\right)\right]\cdots \mathrm{①}$$が言えて、$f(x)$の小数部分が$\sqrt{⟨x⟩}$に一致すること、つまり、$$⟨f(x)⟩=\sqrt{⟨x⟩}\cdots \mathrm{②}$$が言えます。

ここで、①式において $x=f^{-1}(y^2)$（$y^2=f(x)$ とするのと同じ）とすると、$$\left[y^2\right]=[f^{-1}(y)]\cdots \mathrm{③}$$を得ます。

また、②式より、両辺正より2乗して$$⟨f(x){⟩}^2=⟨x⟩$$となり、$x=f^{-1}(y)$ を代入してやると$$⟨y{⟩}^2=⟨f^{-1}(y)⟩\cdots \mathrm{④}$$を得ます。

よって、③と④より、$$\begin{array}{rl}{f}^{-1}(y)& =[f^{-1}(y)]+⟨f^{-1}(y)⟩\\ & =\left[y^2\right]+⟨y{⟩}^2\end{array}$$を得るので、変数を$x$にすれば、逆関数$f^{-1}(x)$は$$f^{-1}(x)=\left[x^2\right]+⟨x{⟩}^2$$と表せます。

これをグラフにすると以下の赤線のようになります（灰色の線は $y=x^2(x\geqq 0)$ のグラフ）。

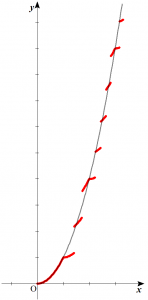
今回の問題を解く上では全く気付く必要の無いことですが、実は $k\leqq x<k+1$（$k$は非負整数）の範囲で $y=f^{-1}(x)$ のグラフは $2k+1$ 個の領域に分割されています。

これはデジタル（離散的）なグラフとなる $y=\left[x^2\right]$（青色）を考えれば明らかで、$y=⟨x{⟩}^2$ のグラフ（緑色）も描くと以下のようになります。

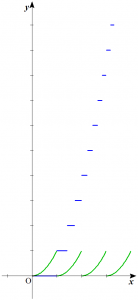
$x^2$の整数部分を$n$とすると、$$n\leqq x^2<n+1$$ $$\therefore \sqrt{n}\leqq x<\sqrt{n+1}$$が成り立ちます。つまり、$\sqrt{n}$が整数$k$となるとき $n=k^2$ となり、$\sqrt{n}$が次の整数 $k+1$ となるのは $n=(k+1{)}^2$ のときであるため、その間にはちょうど$$(k+1{)}^2-k^2=2k+1$$だけ整数が存在します。

そのため、$y=f^{-1}(x)$ のグラフは $k\leqq x<k+1$ の範囲で $2k+1$ 個の曲線に分割されています。ただし、$x$が整数となる点では $y=f^{-1}(x)$ のグラフは連続になっているので、$y=f^{-1}(x)$ のグラフには $k\leqq x<k+1$（$k\geqq 1$）の範囲に不連続な箇所が $2k-1$ 個あることが分かります。

 

 この問題の作り方

ここまで見てきたように本問では逆関数が先にあり、$f(x)$の形で出題しているのは、わざと題意を分かりにくくするためであると推測できます。実際、$f(x)$を陽関数のようないわゆる「閉じた形」として表示することは困難です。

---

先ほど導いた$$f^{-1}(y)=\left[y^2\right]+⟨y{⟩}^2\cdots (\ast \ast )$$という式から問題文中の$f(x)$の式を導くのはそれほど難しくありません。少しやってみましょう。

$(\ast \ast )$より、$$f^{-1}(y)-⟨y{⟩}^2=\left[y^2\right]$$となるので、右辺が整数であり、$⟨y{⟩}^2$が$1$未満であることから、$⟨y{⟩}^2$は$f^{-1}(y)$の小数部分であることが分かります。これより、$$⟨y{⟩}^2=⟨f^{-1}(y)⟩$$ $$\therefore ⟨y⟩=\sqrt{⟨f^{-1}(y)⟩}$$を得ます。

また、$(\ast \ast )$より$\left[y^2\right]$は$f^{-1}(y)$の整数部分となるので、$$\left[y^2\right]=[f^{-1}(y)]$$と表せて、$y^2$を$y$で置き換えると$$\left[y\right]=[f^{-1}(\sqrt{y})]$$を得ます（ここで問題文中の条件1、2が効いてくる）。

したがって、$$\begin{array}{rl}y& =\left[y\right]+⟨y⟩\\ & =[f^{-1}(\sqrt{y})]+\sqrt{⟨f^{-1}(y)⟩}\end{array}$$となるから、これに $y=f(x)$ を代入して$$f(x)=\left[f^{-1}\left(\sqrt{f(x)}\right)\right]+\sqrt{⟨f^{-1}(f(x))⟩}$$ $$\therefore f(x)=\left[f^{-1}\left(\sqrt{f(x)}\right)\right]+\sqrt{⟨x⟩}$$が得られます。

･･･という訳で、出題サイドとしては関数$$y=\left[x^2\right]+⟨x{⟩}^2$$を題材に、少し捻って出題した、といった所だと思います。

---