【整式の割り算】組立除法の極意

今回は整式同士で割り算を効率的に計算する方法である「組立除法」(くみたてじょほう) について動画付きで解説します。整式の除算が苦手な人は必見です！

 

 普通の割り算の場合

組立除法について説明する前に、まずは筆算形式の普通の割り算をおさらいしておきましょう（時間が無い人は読み飛ばして結構です）。

次の問題を考えてみます。

次のように解くのが普通でしょうか。

これは次のような手順で計算しています。ごく普通の筆算です。

これでも割り算は実行できますが、$x^{n}$の部分は実質的に不要なので、実はかなり非効率な書き方になってしまっています。

そこで、次のように$x$の部分や「$+$」の符号を省略します。これにより書く手間がかなり減り、計算が効率化できます。$$\small \begin{array}{rr|rrrrr}
 & & & 1 & 5 & 9 & 22 \\
\hline 1 & -2 & 1 & 3 & -1 & 4 & 1 \\
& & 1 & -2 & & \\
\hline & & & 5 & -1 & & \\
& & & 5 & -10 & & \\
\hline & & & & 9 & 4 & \\
& & & & 9 & -18 & \\
\hline & & & & & 22 & 1 \\
& & & & & 22 & -44 \\
\hline & & & & & & 45
\end{array}$$この書き方に慣れておくことを強くオススメします！

 

 組立除法の場合

それではお待ちかねの組立除法の解説をしていきます。

組立除法では、割る方の整式は1次式でなければなりませんが、割られる方の数式は何次の多項式であってもOKです。具体的なやり方は以下の通りです。

これは次のような手順で計算しています。

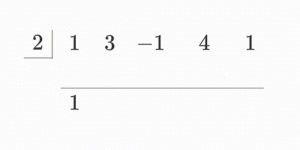
最高位の数字はそのまま下ろしてきます。次々と乗じている$2$は、因数 $x-\color{red}{2}$ の部分に由来しています（この定数を書く位置に関しては色々な流儀があります）。

例えば $x+4$ で割る場合は最下段の数に $-4$ を乗じます。$2x-3$ で割る場合は先に$2$で括り、最下段の数に $\dfrac{3}{2}$ を乗じて計算します。

要するに $x-a$ で割る場合には、同次の項で和を取りつつ、次々と$a$を掛けて計算することになります。手計算の際に筆算をするよりも書く手間が大きく削減されます。

 

 組立除法の仕組み

組立除法で割り算ができる仕組みについて少し説明します。

2次式の割り算で理解するのが分かりやすいと思いますので、整式 $p_0 x^2+p_1 x+p_2 $ を $x-a$ で割る操作を考えます。

普通の筆算なら次のようになります。

$$\small \begin{array}{rr|rrrr}
 & & & p_0 & p_1+ap_0 \\
\hline 1 & -a & p_0 & p_1 & p_2 \\
& & \color{red}{p_0} & -\color{blue}{ap_0} & & \\
\hline & & & p_1+ap_0 & p_2 & \\
& & & \color{red}{p_1+ap_0} & -\color{blue}{a(p_1+ap_0)} & \\
\hline & & & & \color{red}{p_2+a(p_1+ap_0)}
\end{array}$$

これを組立除法の書き方に直すと次のようになります。

$$\small \begin{array}{r|rrrrr}
a \quad & p_0 & p_1 & p_2 \\
& & \color{blue}{ap_0} & \color{blue}{a(p_1+ap_0)} \\
\hline & \color{red}{p_0} & \color{red}{p_1+ap_0} &\!|\!| \ \ \color{red}{p_2+a(p_1+ap_0)} \\
\end{array}$$

青字部分と赤字部分はそれぞれ対応しています。

今は2次式の割り算を考えましたが、何次式の割り算であっても同じ方法で計算できます。

この様子から、組立除法でも普通の筆算と全く同じ計算を行っていることが見て取れるでしょう。筆算の余分な部分を省略した書き方で割り算を行っている、というのが組立除法の本質です。

 

 例題

組立除法の使って幾つか計算練習をしてみましょう。

$$\small \begin{array}{rlr}
\dfrac{\left.-3 \ \right|}{} & {\begin{array}{rrrrr}
1 & -2 & 1 & -2 & 1 \\
& -3 & 15 & -48 & 150 \\
\hline 1 &-5 & 16 & -50 &\!|\!|\ \ \color{red}{151}
\end{array}}
\end{array}$$より、余りは$\color{red}{151}$となります。

 

---

$2x-1$ を$2$で括り、$x-\dfrac{1}{2}$ で割って余りを求めます。後で$2$倍すると商を求めることができます。

$$\small \begin{array}{rlr}
\dfrac{\left.\dfrac{1}{2} \ \right|}{} & {\begin{array}{rrrr}
1 & 0 & 0 & 1 \\
& \dfrac{1}{2} & \dfrac{1}{4} & \dfrac{1}{8} \\
\hline 1 & \dfrac{1}{2} & \dfrac{1}{4} &\left|\!{}\left|\ \ \color{red}{\dfrac{9}{8}}\right.\right.
\end{array}}
\end{array}$$これより、$$\small \begin{align} & \quad \ \ x^{3}+1 \\ &= \left(x^{2}+\frac{1}{2}x+\frac{1}{4}\right) \left(x-\frac{1}{2}\right)+\frac{9}{8} \\ &= \left(\frac{1}{2}x^{2}+\frac{1}{4}x+\frac{1}{8}\right) \left(2x-1\right)+\frac{9}{8} \end{align}$$となるので、商は$\color{red}{\dfrac{1}{2}x^{2}+\dfrac{1}{4}x+\dfrac{1}{8}}$、余りは$\color{red}{151}$となります。

 

---

この問題は組立除法を使うメリットがありませんが、虚数解 $\pm i$ を用いて次のように無理やり計算することはできます。

$$\small \begin{array}{rlc}
\begin{array}{r}\dfrac{\left. i \ \right|}{} \\ \dfrac{\left. -i \ \right|}{}\end{array} & {\begin{array}{rrrr}
1 & 2 & 1 & 1 \\
& i & 2i-1 & -2 \\
\hline 1 & 2+i & 2i &\!|\!| \ \color{red}{-1} \\
& -i & -2i \\
\hline 1 & 2 &\!|\!| \quad \color{red}{0}
\end{array}}
\end{array}$$

これより$$\begin{align} & \quad \ \ x^3+2x^2+x+1 \\ &=(x+2)(x^2+1)-1 \end{align}$$を得るので、商は$\color{red}{x+2}$、余りは$\color{red}{-1}$となります。

 

---