前回の記事では「順像法」と「逆像法」の仕組みについて詳しく解説しました。今回はこれらの解法が実際の入試の場面でどのように使われるのかを見てみます。東京大学の問題を取り上げていますが、東大を受験しない人にも是非取り組んで欲しい良問です。
《問題》
正の実数$a$に対して、座標平面上で次の放物線を考える。$$C: \quad y=a x^{2}+\dfrac{1-4 a^{2}}{4 a}$$ $a$が正の実数全体を動くとき、$C$の通過する領域を図示せよ。
(東京大学2015年 理科第1問)
《考え方》
本問は順像法と逆像法の優れた教材です。数Ⅲの知識は必要になりますが、是非とも授業で取り上げて頂きたい問題です。
領域を図示させる問題は難関大学では頻出です。本問は東大レベルとしては比較的易しめの部類ですが、適度な難度の良問と言えます。この手の問題では「順像法」もしくは「逆像法」を用いて領域を求めることになります。順像法と逆像法については「【順像法と逆像法①】直線の掃過領域を例に理解する」の記事をご覧下さい。
順像法を使う場合は$$y=a x^{2}+\dfrac{1-4 a^{2}}{4 a}$$において $x=t$($t$は定数)などと置いて$x$を固定し、$$y=(t^2-1)a+\dfrac{1}{4a}$$と整理してから$y$の値域を求めます。
逆像法を使う場合は与式を$$(x^{2}-1)a^2-ya+\dfrac{1}{4}=0$$と$a$の二次方程式に変形し、これが実数解を持つ条件から領域を導きます。
いずれの方法でも場合分けが必要となり、あまり手間は変わりません。以下では両方の解き方による解答例を掲載します。
順像法による解答例
与式を$$\begin{aligned}
y &= a x^{2}+\dfrac{1-4 a^{2}}{4 a} \\
&=a x^{2}+\dfrac{1}{4 a}-a \\
&=(x^2-1)a+\dfrac{1}{4a}
\end{aligned}$$と変形する。ここで、$x=t$($t$は定数)と置いて$x$を固定すると、そのときの$y$の値が取り得る範囲は$a$の関数$$f(a)=(t^2-1)a+\dfrac{1}{4a}$$の値域に等しい。以下、係数 $t^2-1$ の正負で場合分けを行い、関数$f(a)$の値域を調べる。
また、$$\begin{aligned}
f^{\prime}(a) &= t^{2}-1-\frac{1}{4 a^{2}} \\
&=\frac{4\left(t^{2}-1\right) a^{2}-1}{4 a^{2}}
\end{aligned}$$であることに注意する。
(ⅰ)$t^{2}-1 \leqq 0$ のとき、$f^{\prime}(a)<0$ となるから $f(a)$ は単調減少である。$$\displaystyle \lim _{a \rightarrow+0} f(a)=\infty$$および$$\displaystyle \lim _{a \rightarrow \infty} f(a)=\left\{\begin{array}{cc}0 & \left(t^{2}-1=0\right) \\ -\infty & \left(t^{2}-1<0\right)\end{array}\right.$$となるから、$y$の値域は$$\left\{\begin{array}{lc}k=\pm 1 \text { のとき、} 0<y \\ -1<k<1 \text { のとき、} y \text { は任意の実数 }\end{array}\right.$$となる。
(ⅱ)$t^{2}-1 > 0$ のとき、導関数$f^{\prime}(a)$は$$\small f^{\prime}(a)=\dfrac{4\left(t^{2}-1\right)}{4 a^{2}}\left(a-\dfrac{1}{2 \sqrt{t^{2}-1}}\right)\left(a+\dfrac{1}{2 \sqrt{t^{2}-1}}\right)$$となり、増減表は次のようになる。$$\small \begin{array}{|c||c|c|c|c|}
\hline a & (0) & \cdots & \dfrac{1}{2 \sqrt{t^{2}-1}} & \cdots \\
\hline f^{\prime}(a) & & – & 0 & + \\
\hline f(a) & (\infty) & \searrow & \sqrt{t^{2}-1} & \nearrow \\
\hline
\end{array}$$ $\displaystyle \lim _{a \rightarrow+0} f(a)=\infty$ および $\displaystyle\lim _{a \rightarrow \infty} f(a)=\infty$ を合わせると、$y$の値域は$$y \geqq \sqrt{t^{2}-1}$$となる。
以上(ⅰ)と(ⅱ)の結果から、放物線$C$の通過する領域は以下の斜線部のようになる。ただし、境界線は $y = \sqrt{x^{2}-1}$($y>0$)の部分のみ含む。
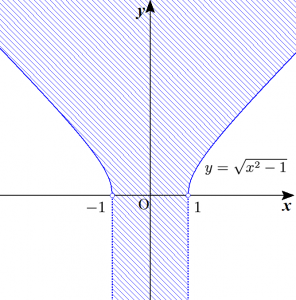
順像法はどんな問題に対しても使えるオールマイティな解法です。基本的には順像法をまずマスターしておくべきです。
一方で、本問の放物線の方程式は$a$の二次方程式に式変形することができます。このような場合、通過領域の決定を二次関数の解の配置問題に帰着させる逆像法を用いて解答することも可能です。
以下、逆像法による解答例を示します。
逆像法による解答例
放物線$C$の方程式は$$y = a x^{2}+\dfrac{1-4 a^{2}}{4 a}$$ $$\therefore (x^2-1)a^2-ya+\dfrac{1}{4}=0$$と変形できる。これより、$C$が点$(X,Y)$を通過するような実数$a$が存在するための条件は、$a$に関する方程式$$(X^2-1)a^2-Ya+\dfrac{1}{4}=0 \quad \cdots ①$$が正の実数解$a$を少なくとも1つもつ条件に一致する。
以下、$f(a)=(X^2-1)a^2-Ya+\dfrac{1}{4}$ と置いて方程式$①$が正の実数解をもつ条件を調べる。なお、$$f(0)=\dfrac{1}{4} \quad \cdots ②$$であることに注意する。
(ⅰ)$X^2-1=0$、即ち $X=\pm 1$ のとき、$$f(a)=-Ya+\dfrac{1}{4}$$ となるから、このとき $f(a)=0$ が正の実数解をもつためには傾き $-Y$ が負でなければならない。したがって、$$Y>0$$が求める条件となる。
(ⅱ)$X^2-1<0$ のとき、$b=f(a)$ は$ab$平面上で上に凸な放物線となる。$②$を考慮すると $f(a)=0$ は正の実数解を1つもつ。故に、任意の$Y$が適する。
(ⅲ)$X^2-1>0$ のとき、$b=f(a)$ は$ab$平面上で下に凸な放物線となる。このとき$$\small f(a)=\left(X^{2}-1\right)\left\{a-\frac{Y}{2\left(X^{2}-1\right)}\right\}^{2}-\frac{Y^{2}}{4\left(X^{2}-1\right)}+\frac{1}{4}$$と変形する。$②$を考慮すると、軸について$$\frac{Y}{2\left(X^{2}-1\right)}>0 \quad \cdots ③$$が成り立つことが必要である。また、頂点について$$-\frac{Y^{2}}{4\left(X^{2}-1\right)}+\frac{1}{4} \leqq 0 \quad \cdots ④$$となることが必要である。
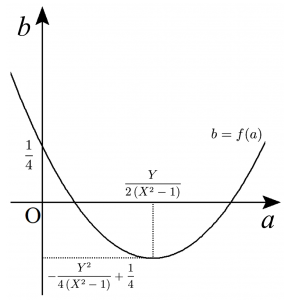
$X^2-1>0$ のとき、$③$かつ$④$は
$Y>0$ かつ $X^2-Y^2 \leqq 1$
と同値である。
以上(ⅰ)~(ⅲ)の結果から、放物線$C$の通過する領域は以下の斜線部のようになる。ただし、境界線は $y = \sqrt{x^{2}-1}$($y>0$)の部分のみ含む。

因みに本問の放物線$C$をグラフ化すると下図のようになります。横のスライダーで$a$の値を色々変えられます。
それぞれの解答はどちらの方が優れているというものではなく、利点も欠点もあります。問題によっては順像法の方がラクだったり、逆像法の方がラクだったりします。臨機応変に対応できるように両方の解法をマスターしておくべきです。
通過領域や軌跡を求める問題では、答案の中で$x$や$y$だけでなく色々な文字を使う必要が出てきます。問題集の解答例を読むときにこんがらがってしまいがちですが、基本的には解答を分かりやすくするために便宜上用いているだけです。
例えば「逆像法による解答例」ではいきなり$ab$平面が登場していますが、$b$という文字を使う必然性は無く、$u=f(a)$ と置いて$au$平面上で議論しても全く問題ありません。元々、放物線$C$は$xy$平面上で考えているので、それとは別に$a$を軸とする別の平面上で$f(a)$のグラフを考えていますよ、ということが答案の読み手に伝わる書き方になっていれば何でもOKです。
本問はセオリー通りの方法で素直に解けます。東大を目指している方は、この程度の問題はサラッと解けるようにしておきましょう。世の中にはもっと複雑な領域を求める問題が沢山ありますが、解き方の基本はどれも同じであり、類題の経験がモノを言います。彼を知り己を知れば百戦殆うからず、ですね!

“【順像法と逆像法②】放物線の掃過領域(東京大学2015年)” への1件の返信