前回の続きです。ケンブリッジ大学の入学試験に利用されている「Sixth Term Examination Paper」(通称 STEP) から、2019年のSTEP1第2問をご紹介します。
《問題》
The curve $C$ is given parametrically by the equations $x = 3t^2$, $y = 2t^3$. Show that the equation of the tangent to $C$ at the point $(3p^2 , 2p^3)$ is $y = px − p^3$.
Find the point of intersection of the tangents to $C$ at the distinct points $(3p^2 , 2p^3)$ and $(3q^2 , 2q^3)$. Hence show that, if these two tangents are perpendicular, their point of intersection is $(u^2 + 1, −u)$, where $u = p + q$.
The curve $\tilde{C}$ is given parametrically by the equations $x = u^2 + 1$, $y = −u$. Find the coordinates of the points that lie on both $C$ and $\tilde{C}$. Sketch $C$ and $\tilde{C}$ on the same axes.
(STEP2019 MATHⅠ §A p2)
» 和訳はこちら
曲線$C$は、方程式 $x = 3t^2$, $y = 2t^3$ によって媒介変数表示される。点 $(3p^2 , 2p^3)$ における$C$の接線の方程式は、$y=px-p^3$ であることを示せ。
異なる2点 $(3p^2 , 2p^3)$ および $(3q^2 , 2q^3)$ における$C$の接線の交点を求めよ。これにより、これら2つの接線が垂直であれば、その交点は $(u^2 + 1, -u)$ となることを示せ。ただし $u = p + q$ である。
曲線$\tilde{C}$は、方程式 $x = u^2 + 1$, $y = -u$ によって媒介変数表示される。$C$と$\tilde{C}$の両曲線上にある点の座標を求めよ。さらに$C$と$\tilde{C}$を同じ座標平面上に描け。
» 閉じる
《考え方》
媒介変数表示された曲線に関する問題です。日本だと数Ⅲに分類されるレベルの問題ですね。
曲線$C$はすぐに求められると思います。誘導にしたがって直交する接線の条件から交点を求め、曲線$\tilde{C}$を求めましょう。グラフを描くときは尖点(せんてん)や、$C$と$\tilde{C}$が接することなどに注意して下さい。
解答例
接線について
$$\small \dfrac{d y}{d x}=\dfrac{\dfrac{d}{d t}\left(2 t^{3}\right)}{\dfrac{d}{d t}\left(3 t^{2}\right)}=\dfrac{6 t^{2}}{6 t}=t$$ より、点 $\mathrm{P}(3p^2 , 2p^3)$ における接線の傾きは $p$ となる。このとき接線の方程式は$$y-2 p^{3}=p\left(x-3 p^{2}\right)$$つまり$$y=p x-p^{3}$$となる。
2接線の交点について
$y=p x-p^{3}$ と $y=q x-q^{3}$ が交点を持つとき、$$p x-p^{3}=q x-q^{3}$$ $$\therefore x=\left(p^{3}-q^{3}\right)$$が成り立ち、$p \ne q$ より$$\begin{cases} x=p^{2}+p q+q^{2} \\ y=p q(p+q) \end{cases} \quad \cdots (*)$$と表せる。
いま2つの接線が直交するから、$p q=-1$ であり、このとき$$\small u=p-\dfrac{1}{p},\, u^{2}=p^{2}+\dfrac{1}{p^{2}}-2$$となるから$(*)$より$$\small \begin{align} P&=\left(p^{2}+\frac{1}{p^{2}}-1,\,-1 \cdot \left(p-\frac{1}{p}\right)\right) \\ &=\left(u^{2}+1,-u\right) \end{align}$$となる。
曲線$\tilde{C}$について
曲線 $\tilde{C}:x=y^{2}+1$ が曲線 $C:\dfrac{x^{3}}{27}=\dfrac{y^{2}}{4}$ と交点をもつとき、$$\dfrac{(y^{2}+1)^{3}}{27}=\dfrac{y^{2}}{4}$$ $$\therefore 4\left(y^{2}+1\right)^{3}=27 y^{2}$$ $$\therefore 4\left(y^{6}+3 y^{4}+3 y^{2}+1\right)=27 y^{2}$$ $$\therefore 4 y^{6}+12 y^{4}-15 y^{2}+4 =0$$ $$\therefore \left(y^{2}+4\right)\left(4 y^{4}-4 y^{2}+1\right) =0$$ $$\therefore \left(y^{2}+4\right)\left(2 y^{2}-1\right)^{2} =0$$となるから、$y^{2}=\dfrac{1}{2}$ より、$$y=\pm \dfrac{1}{\sqrt{2}},\, x=\dfrac{3}{2}$$と求められる。よって求める交点の座標は$$\left(\dfrac{3}{2},\, \pm \dfrac{1}{\sqrt{2}}\right)$$となる。
曲線 $\tilde{C}:x=y^{2}+1$ は放物線であり、曲線 $C:\dfrac{x^{3}}{27}=\dfrac{y^{2}}{4}$ については$$\small \dfrac{d y}{d x}=t \ \left(=\pm \sqrt{\dfrac{x}{3}}=\sqrt[3]{\dfrac{y}{2}}\right)$$ より、$y>0$ の部分では傾きが単調増加、$y<0$ の部分では傾きが単調減少となる。また交点$\small \left(\dfrac{3}{2},\, \pm \dfrac{1}{\sqrt{2}}\right)$では$C$と$\tilde{C}$が接している。
以上から、曲線の概形は以下のようになる。ただし赤色の曲線が$C$、青色の曲線が$\tilde{C}$である。
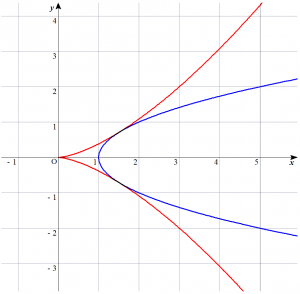
(コメント)
前回に引き続き、イギリスの難関大学の入試問題を取り上げましたが、本問に関しても普通の数Ⅲの問題という印象ですね。かなり誘導が丁寧なので、ささっと片付けたいところです。
取り敢えず2問分解説してみましたが、誰得企画ですね・・・(笑)
