創作整数問題#62解法＆創作整数問題#63

解答例

曲線$C_1$：$y=x^2$ を$45^{\circ}$だけ反時計回りに回転させて得られる曲線を$C_a$、反対に$45^{\circ}$だけ時計回りに回転させて得られる曲線を$C_b$とする。このとき曲線の位置関係は下図のようになり、$C_a$と$C_b$は$y$軸に関して対称であるから、$C_a$上の格子点の$x$座標の符号を反転した点は$C_b$上の格子点となる。よって$C_a$上の格子点を探せば十分である。

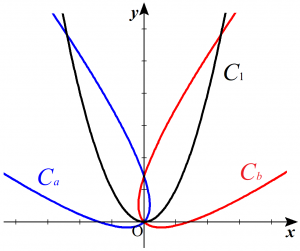
以下、曲線$C_a$の方程式を求める。$C_a$の方程式は、パラメータ表示された複素数 $t+t^2 i$ に対して $\cos 45^{\circ}+i \sin 45^{\circ}$ を乗じることで得られる。$$\begin{align}& (t+t^2 i)(\cos 45^{\circ}+i \sin 45^{\circ}) \\ =\,& (t+t^2 i)\left(\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{2}}i\right) \\ =\,& \dfrac{\sqrt{2}}{2}(t+t^2 i)(1+i) \\ =\,& \dfrac{\sqrt{2}}{2}(t-t^2)+\dfrac{\sqrt{2}}{2}(t+t^2)i\end{align}$$となり、この回転操作によって曲線$C_1$上の点$(t,t^2)$が移される点を$(X,Y)$と置くと$$\begin{cases} X=\dfrac{\sqrt{2}}{2}(t-t^2) \\ Y=\dfrac{\sqrt{2}}{2}(t+t^2) \end{cases}$$と表せる。これより、$$X+Y=\sqrt{2}\,t$$ $$\therefore t=\dfrac{1}{\sqrt{2}}(X+Y)$$となるので$t$を消去して整理すると、$$X^2+2XY+Y^2+\sqrt{2}X-\sqrt{2}Y=0$$を得る。よって曲線$C_a$の方程式は$$x^2+2xy+y^2+\sqrt{2}x-\sqrt{2}y=0$$となる。これより点$(0,0)$は明らかに曲線$C_a$上の格子点である。

以下、$x \ne 0$ かつ $y \ne 0$ かつ $x \ne y$ とすると、$$(x+y)^2+\sqrt{2}(x-y)=0$$ $$\therefore \dfrac{(x+y)^2}{(y-x)}=\sqrt{2} \quad \cdots (*)$$と変形できる。ここで以下の補題を示す。

よって補題より$(*)$の右辺は無理数であり、$x$、$y$が整数のとき$(*)$の左辺は有理数であるから、$(*)$を満たす整数の組$(x,y)$は存在しない。

以上より、求める$C_2$上の格子点は$$(x,y)=\color{red}{(0,0)}$$である。