各種三角関数のマクローリン展開

この記事では各種三角関数のマクローリン展開（x=0におけるテイラー展開）を扱います。20次までの展開式一覧も掲載しています。

 

 三角関数のマクローリン展開

$$\small \displaystyle \begin{align} \sin x &= \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1} \\ &=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \end{align}$$ $$\small \displaystyle \begin{align} \cos x &=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n} \\ &=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots \end{align}$$ $$\small \displaystyle \begin{align} \tan x &=\sum _{n=1}^{\infty }{\frac {B_{2n}(-4)^{n}\left(1-4^{n}\right)}{(2n)!}}x^{2n-1} \\ &=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+{\frac {17x^{7}}{315}}+\cdots \end{align}$$（$B_n$ はベルヌーイ数）

これより、$\sin x$ を微分すると $\cos x$ になり、$\cos x$ を微分すると $-\sin x$ になることが直感的に見て取れます。

また、展開を打ち切る次数が大きいほど元の関数を正確に表現できます（下図参照）。

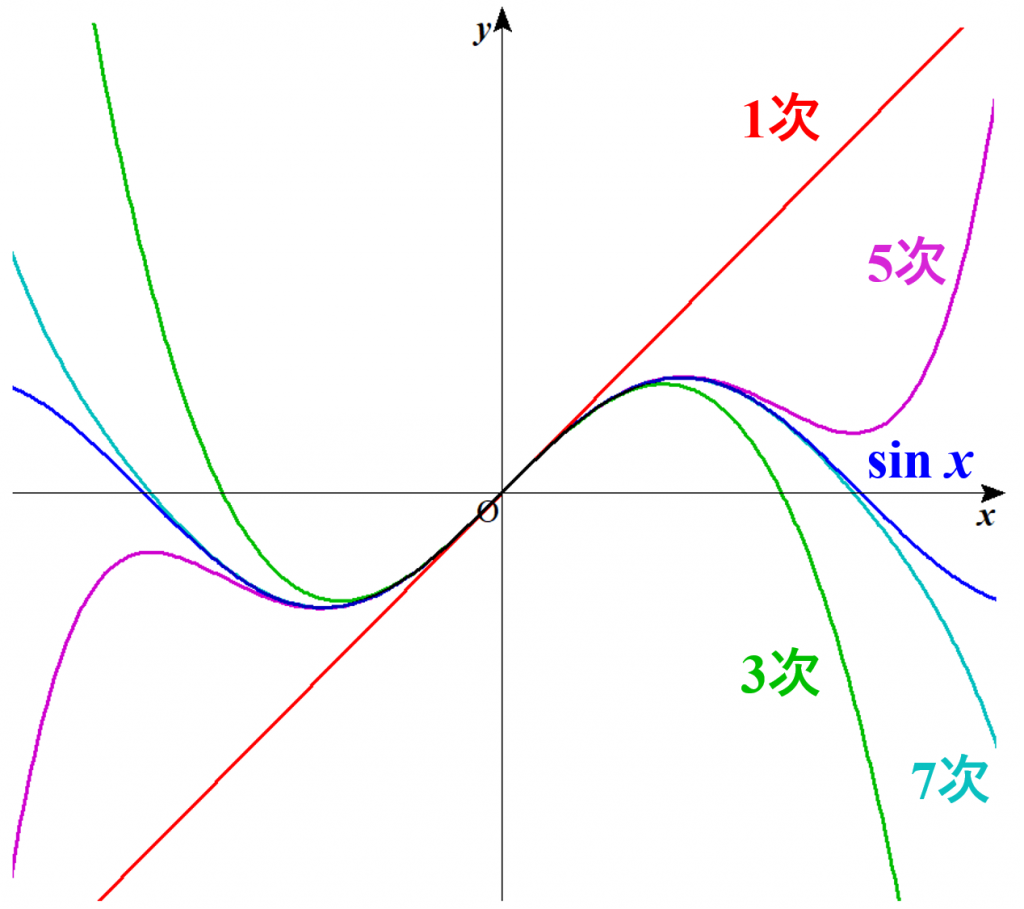図．$\sin x$ のマクローリン展開

 

 逆三角関数のマクローリン展開

$$\small \displaystyle \begin{aligned}\arcsin x&=\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1} \\ &=x+{\frac {x^{3}}{6}}+{\frac {3x^{5}}{40}}+{\frac {5x^{7}}{112}}+\cdots \\ \arccos x&={\frac {\pi }{2}}-\arcsin x \\ &={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1} \\ &={\frac {\pi }{2}}-x-{\frac {x^{3}}{6}}-{\frac {3x^{5}}{40}}-{\frac {5x^{7}}{112}}-\cdots \\[6pt]\arctan x &=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1} \\ &=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-{\frac {x^{7}}{7}}+\cdots \end{aligned}$$ここで、$\arcsin x=\sin^{-1}x$ のことを指します。他も同様です。

 

 20次までの展開式

$\small \begin{align} \sin x &= x-\dfrac{x^{3}}{6}+\dfrac{x^{5}}{120}-\dfrac{x^{7}}{5040}+\dfrac{x^{9}}{362880} \\ &\quad -\dfrac{x^{11}}{39916800}+\dfrac{x^{13}}{6227020800}-\dfrac{x^{15}}{1307674368000} \\ &\quad +\dfrac{x^{17}}{355687428096000}-\dfrac{x^{19}}{121645100408832000}+O(x^{20}) \end{align}$

$\small \begin{align} \cos x &= 1-\dfrac{x^{2}}{2}+\dfrac{x^{4}}{24}-\dfrac{x^{6}}{720}+\dfrac{x^{8}}{40320}-\dfrac{x^{10}}{3628800} \\ &\quad +\dfrac{x^{12}}{479001600}-\dfrac{x^{14}}{87178291200}+\dfrac{x^{16}}{20922789888000} \\ &\quad -\dfrac{x^{18}}{6402373705728000}+\dfrac{x^{20}}{2432902008176640000}+O(x^{22}) \end{align}$

$\small \begin{align} \tan x &= x+\dfrac{x^{3}}{3}+\dfrac{2 x^{5}}{15}+\dfrac{17 x^{7}}{315}+\dfrac{62 x^{9}}{2835} \\ &\quad +\dfrac{1382 x^{11}}{155925}+\dfrac{21844 x^{13}}{6081075}+\dfrac{929569 x^{15}}{638512875} \\ &\quad +\dfrac{6404582 x^{17}}{10854718875}+\dfrac{443861162 x^{19}}{1856156927625}+O(x^{20}) \end{align}$

$\sin x$ や $\cos x$ は分母が階乗なので特に書き下す必要はありませんが、$\tan x$ の展開式計算は手計算だとそれなりに骨が折れます。

---