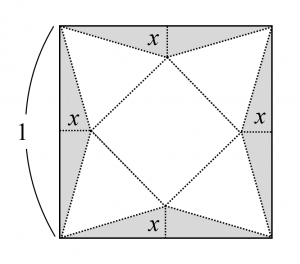
四角錐の展開図の切り出し（名古屋市立大学2014年）

解答例

$x$の範囲は $0<x<\dfrac{1}{2}$ であることに注意する。

四角錐の底面は対角線の長さが $1-2x$ の正方形であり、その面積は $\dfrac{1}{2}(1-2x)^2$ となる。側面の二等辺三角形の等しい辺（底辺でない方の辺）の長さは $\sqrt{x^{2}+\dfrac{1}{4}}$ であるから、四角錐の高さは三平方の定理より$$\sqrt{x^{2}+\dfrac{1}{4}-\left(\dfrac{1}{2}-x\right)^{2}}=\sqrt{x}$$と求められる。

故に四角錐の体積$V$は$$\begin{aligned}
V &=\dfrac{1}{3} \sqrt{x} \cdot \dfrac{1}{2}(1-2 x)^{2} \\
&=\dfrac{\sqrt{x}(1-2 x)^{2}}{6}
\end{aligned}$$で与えられる。ここで、導関数は$$\begin{aligned}
\dfrac{d V}{d x} &=\dfrac{\dfrac{1}{2 \sqrt{x}}(1-2 x)^{2}-4 \sqrt{x}(1-2 x)}{6} \\
&=\dfrac{(1-2 x)(1-10 x)}{12 \sqrt{x}}
\end{aligned}$$となるから、増減表は以下のようになる。$$\begin{array}{|c||c|c|c|c|c|}
\hline x & 0 & \cdots & \dfrac{1}{10} & \cdots & \dfrac{1}{2} \\
\hline \dfrac{d V}{d x} & & + & 0 & – & \\
\hline V & & \nearrow & \dfrac{4 \sqrt{10}}{375} & \searrow & \\
\hline
\end{array}$$よって$V$は $x=\color{red}{\dfrac{1}{10}}$ のとき、最大値$$\color{red}{\dfrac{4 \sqrt{10}}{375}}$$をとる。