2021年6月16日2022年11月25日投稿者: pencil

回文数の性質について

今日は6/16。616は左から読んでも右から読んでも616。･･･ということで、今回は「回文数」に関する話題を取り上げてみます。

回文数とは

回文数（かいぶんすう；Palindromic number）とは、各位の数を反転させてできる整数と元の整数が同じであるようなものを指します。例えば、$121$や$4385834$などは回文数です。

そもそも「回文」とは、「新聞紙」や「竹やぶ焼けた」のように、順番をひっくり返しても全く同じように読める語や文のことを指しています。整数値についても、そのアナロジーから「回文数」という名前で呼ばれています。英語で回文は “palindrome” であり、回文数は “Palindromic number” と呼ばれています。中国語では日本と全く同じ「回文数」という名称で呼ばれています。

$n$桁の回文数の個数

$n$桁の回文数の個数は

9, 9, 90, 90, 900, 900, 9000, 9000, …

という数列を成します。これはオンライン整数列辞典「OEIS」にA050683として登録されています。回文数自体はOEISのA002113として登録されています。

一般項$a_n$は $$a_n=9 \cdot 10^{\lfloor(n-1)/2\rfloor}$$で与えられ、$$a_{n}=10 a_{n-2}$$という漸化式が成り立ちます。ここで$\lfloor(n-1)/2\rfloor$は床関数で、$(n-1)/2$を超えない最大の整数を表しています。

$2k$ 桁の回文数は、最上位の数が$0$にならないように上$k$桁の数を決めれば自動的に決まります。また、$2k+1$ 桁の回文数は、左右中央の桁の数字を$0$～$9$のうちから選び、最上位の数が$0$にならないように上$k$桁の数を決めれば自動的に決まります。このことから、上記の一般項が導かれます（奇数桁とその次の偶数桁の回文数の個数が同じになるのはこのような理由によります）。

偶数桁の回文数は$11$の倍数

鋭い数学的センスの持ち主であれば、偶数桁の回文数が「左右対称」であることからすべて$11$の倍数であることを見抜いてしまうかもしれません。

例えば、$100001$のように両端の数字が$1$で真ん中に$0$が偶数個だけ挟まっているような整数は$11$で割り切れます。これは$n$を正の整数として $10^{2n-1}+1$ を$11$で割った余りを合同式で考えれば納得できます。あるいは合同式を使わなくても、このような数が$11+99…990$（$9$が偶数個）と書き直せることからも、偶数桁の回文数が$11$で割り切れることが説明できます。

偶数桁の回文数はこのような整数に$1$～$9$までの整数を乗じたものを幾つか足し合わせた和になっているので、常に$11$の倍数となります。これより、3桁以上の回文素数はすべて奇数桁（偶数桁の回文素数は$11$のみ）であることが従います。過去に数学検定でこの事実に関する問題が出題されているようです。

※因みに、2021年現在の時点で知られている最大の回文素数は$$10^{474500}+999 \times 10^{237249}+1$$です。上位20位までの回文素数がこちらのサイトにまとめられています。

また、$11$の倍数であるような回文数を数え上げさせる問題が最近のジュニア数学オリンピックに出題されています。

正の整数であって、一の位が$0$でなく、一の位から逆の順番で読んでも元の数と等しいものを回文数とよぶ。$10000$以下の正の整数のうち、$11$の倍数であるような回文数はいくつあるか。

（2020年日本ジュニア数学オリンピック予選第3問）

» 答えはこちら

正解は$107$個です。

» 閉じる

それから、かなり古いですがもっと難しい問題が算数オリンピックに出題されています。

ある$6$桁の回文数は、$95$で割り切れ、しかも、その商も回文数になるという。このような回文数をすべて求めよ。

（1995年日本算数オリンピック予選第3問）

» 答えはこちら

正解は$527725$です。因みに、$10^{10}$以下のものは以下の8個のみです。

5225、52725、527725、5277725、52255225、52777725、522505225、527777725

» 閉じる

大学入試だと、これも古いですが2001年の津田塾大の数学に、$11$で割り切れるような$5$桁の回文数のうちで最大のものと最小のものを求めさせる問題が出題されています。オマケ問題として付いていた設問ですが、これに関しては誘導設問を無視した方が寧ろ解きやすいのではないかと思います。

回文数の逆数からなる無限級数は収束する

$1$～$10^k$までの回文数の逆数の和を計算したものを以下に示します。

上限 $10^k$	逆数の和 the sum of the reciprocals
$10$	2.8289682539682537
$10^2$	3.0861471861471856
$10^3$	3.3190020006509102
$10^4$	3.3421302129563510
$10^5$	3.3651662022380453
$10^6$	3.3674689702500697
$10^7$	3.3697715736297990
$10^8$	3.3700018324036383
$10^9$	3.3702320909393553

回文数の逆数からなる無限級数は大体 $3.370283…$ という値に収束することが知られています。ただし、無限級数が収束するからといって回文数が有限個しかない訳ではありません。回文数は無数に存在します。

※参考：A118031 Decimal expansion of the sum of the reciprocals of the palindromic numbers

※逆数の和はプログラムで計算しています。以下はJulia言語でのコード例です。あまり数学的な方法ではないですが･･･。

# sum of the reciprocals of the palindromic numbers
function palindromic_rcplsum()
    sum = 0
    for m = 1:10^5
        rev = parse(Int,reverse(string(m)))
        if rev == m
            sum += 1/rev
        end
    end
    println(sum)
end
palindromic_rcplsum()

全ての整数は高々3つの回文数の和で表せる

2017年に投稿された “Every positive integer is a sum of three palindromes” という論文によれば、5進法以上の記数法上では全ての整数が高々3つの回文数の和で表せることがアルゴリズムとともに示されています。$0$も回文数に含んでいるので自明な組は多いのですが、例えば$23805$であれば

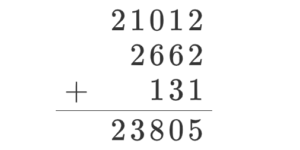
のように3つの回文数の和で表せます。気になる方は “Sum of 3 Palindromes” というページで遊んでみてはいかがでしょう。

なお、”Sums of Palindromes: an Approach via Automata” という別の論文によれば、2進法～4進法の場合は高々4つの回文数で表せるそうです。

※「高々3つの回文数の和で表せる」と主張しているだけで一意性については何も保証していません。実際、「3つの回文数」として適する回文数の組は多くの場合、複数通り存在しています。

参考：
【論文】Every positive integer is a sum of three palindromes
【論文】Sums of Palindromes: an Approach via Automata
（右側の “PDF” (スマホなら”PDF”か”Download PDF”) をクリックすれば論文の内容が読めます）
【動画】Every Number is the Sum of Three Palindromes – Numberphile

「リクレル数」と「196問題」

ある整数に対して各位の数字を反転させてできる数を「逆順数」と呼ぶことにします。ただしこれは一般的な名称ではないので注意して下さい。

ある整数に対して、自身とその逆順数との和を求める操作のことを「リクレルプロセス」と呼びます。例えば、$56$なら$$56 + 65 = 121$$となり、$125$なら$$125 + 521 = 646$$となります。これが１回のリクレルプロセスに相当します。

多くの数はリクレルプロセスを繰り返し適用すると、いずれは回文数になります。特に、1桁と2桁の数字は全て、リクレルプロセスを繰り返すと最終的に回文数になることが知られています。

※リクレルプロセスは以下のように計算できます。Julia言語でのコード例を示しておきます（最大1000回で打ち切り）。この例では$195$をリクレル関数に代入しています。

# Lychrel function
function Lychrel(n)
    count = 0
    for m = 1:1000 # 回数上限
        rev = parse(BigInt,reverse(string(n)))
        if rev == n
            count = m
            break
        else
            println(n)
            n += rev
        end
    end
    println("---------------\n", n, " : ", count-1)
end
Lychrel(195)   # 任意の整数

# 195
# 786
# 1473
# 5214
# ---------------
# 9339 : 4

ここで、何回リクレルプロセスを繰り返しても回文数にならない整数のことを「リクレル数」と呼びます。しかしこれはあくまでも定義でしかなく、十進数におけるリクレル数の存在は証明されていません。つまり「十進数のリクレル数は存在するのか？」という問いは数学の未解決問題なのです。

※$2$進数や$16$進数など、基数が$2$の累乗となっている記数法についてはリクレル数の存在が証明されています。他にも$11$進数、$17$進数、$20$進数、$26$進数について、それぞれリクレル数の存在が証明されています。

十進数の場合は証明ができていないだけで、リクレル数の候補は幾つか知られています。例えば、$196$などはリクレル数であると予想されています。

十進数における$196$は最小のリクレル数の候補であるため、リクレル数か否かについて特に注目されています。$196$がリクレル数か否かを判断する問題には「196問題」と特別に名前が付けられています。数十億回の反復後でも未だに回文は得られていないようです。リクレル数の存在を証明する一般的な方法を思い付いた方は是非とも論文にして発表して下さい･･･。

※Romain Dolbeau氏のページからソースコードをダウンロードすれば「196問題」の分散コンピューティングに協力できるみたいです。

※「196問題」は「コラッツ予想」と似たような未解決問題と言えます。仕組み自体は簡単に理解できるのに、あっという間に未解決問題が登場してしまうのが数論の面白いところですね。この辺りの内容は幾らでも掘り下げられそうです。