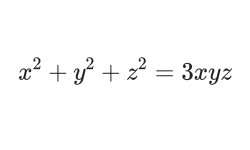しばらく放ったらかしにしてしまいました。創作整数問題シリーズも75回を重ね、これでシーズン3が一区切りします。
マルコフ方程式の解の構成(2006年東京大学前期理系数学第4問)
今回は一昔前の東大理系数学で出題された不定方程式に関する整数問題を取り上げます。
マルコフ数を構成する方法
今回は整数論の分野から「マルコフ数」の話題を取り上げてみます。
【数学夏祭り】第一問(整数問題)の解説【2020年夏】
実は、今週から2週間にわたって「数学夏祭り」という数学愛好家向けのイベントがネット上(主にTwitter上)で開催されています!
問いの花火打ち上がる
世界で一番mathい夏
数学夏祭り
8/31(月) 17:00 第一問 開始#数学夏祭り pic.twitter.com/R5JJPpYF9B— 数学夏祭り@8/31 17時開幕 (@mathmatsuri) August 29, 2020
なんと今回の企画では解説記事も応募対象になっており、しかも第1問は管理人の大好きな整数分野からの出題ということなので、当サイトでも参加してみたいと思います(笑)。25時が解答応募の締め切りということなので、記事の公開は25時ちょうどとしました。
a^2+b^2+c^2=d^2を満たす整数組(一橋大学1994年後期第1問)
昨日に引き続き、方程式 a2 + b2 + c2 = d2 を満たす整数組の剰余に関する問題を取り上げます。
a^2+b^2+c^2=d^2を満たす整数組(横浜国立大学2000年前期(経済)第1問)
今回は表題の通り、a2 + b2 + c2 = d2 という方程式を満たす整数組の剰余に関する問題を取り上げます。
x+yとx+2yがともに平方数となる整数x,y
先日公開した創作整数問題#67に関する話題です。ペル方程式に関する考察(雑談)をしてみます。
3元3次式の整数問題(旭川医科大学2015年数学第1問)
旭川医科大学の前期試験から3元3次式の整数問題を取り上げます。
東北大学2020年前期数学(文系第2問,理系第3問)
今回は東北大学の整数問題を取り上げます。指数関数を含むディオファントス方程式が題材で、文理共通の出題でした。
x^3+y^3+z^3=kの整数解【頭脳王の問題から】
最近話題になった頭脳王の整数問題を取り上げてみます。この問題、実はそれなりに背景のある問題なのです・・・。