√2が無理数であることの証明は高校数学では「背理法」の導入として使われることが多いですが、図形的な証明が可能であることはあまり知られていません。この方法は「無限降下法」の分かりやすい題材になると思うので、教育的観点から取り上げてみます。
早速、証明してみましょう。
まず以下のように、斜辺が$\sqrt{2}$(等辺が$1$)の直角二等辺三角形を考えます。
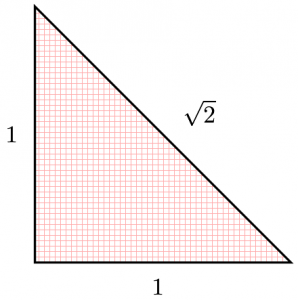
ここで $\sqrt{2}$ が有理数であると仮定します。つまり、互いに素な正の整数 $p$、$q$ を用いて$$\sqrt{2}=\dfrac{p}{q}$$と置きます。
この「$\sqrt{2}$ が有理数である」という仮定は、
仮定の言い換え$(*)$
$\dfrac{p}{q}$という有理数が既約(これ以上約分できない形)であり、組$(p,q)$が$\sqrt{2}$を表現できる最小の整数組として一意に定まる
ということを意味しています。
この仮定を図形的な視点から否定するのが今回のテーマです。
● ● ●
この仮定より、三角形を$q$倍に相似拡大すると、以下のように斜辺が$p$で等辺が$q$の直角二等辺三角形となります。
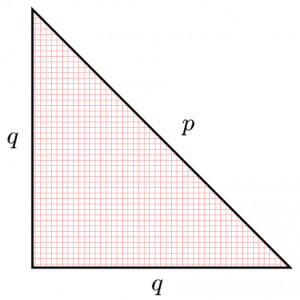
このとき三角形の各辺は整数であることに注意して下さい。なお、この三角形の最小性は上記の$(*)$によって保証されており、この三角形に対してどのような相似縮小を施しても全ての辺が整数になることはありません(この点が証明の核心部分に関連します)。
次に、以下のように三角形の内部から新たに相似な直角二等辺三角形を切り出します。

赤チェック地の三角形 $T_1$ に対して、青斜線地の三角形 $T_2$ の相似比を考えると$$T_1:T_2=q:p-q$$となります。よって、$T_2$ の等辺は $p-q$ となり、$T_1$ の底辺は $q$ なので $T_2$ の斜辺の長さは $q-(p-q)=2q-p$ となります。
しかし、図より明らかに $T_2<T_1$ であり、しかも三角形 $T_2$ の各辺は整数となるので、三角形 $T_1$ の最小性に矛盾します。つまり、$(p,q)$より小さい整数組$(2q-p,p-q)$によって$$\sqrt{2}=\dfrac{2q-p}{p-q}$$と表されることを示しており、組$(p,q)$が$\sqrt{2}$を表現できる最小の整数組である、という仮定に矛盾しています。
したがって仮定は誤りで、$\sqrt{2}$ が無理数であることが従います。
(コメント)
はじめに最小性を仮定し、さらに小さい組が構成できることを示して矛盾を導く、という間接証明法は「無限降下法」と呼ばれます。
今回では三角形の最小性を仮定しましたが、これは$\sqrt{2}$を表現できる幾らでも小さい整数組が構成できる、という点がポイントになっています。要は、青斜線地の三角形 $T_2$ に対して全く同様に新たな相似な三角形 $T_3$ を作ることができる、ということです。今回紹介した構成法では、原理的にはより小さな三角形を幾らでも(=無限個)作ることができますが、正の整数は幾らでも小さく取ることはできないので矛盾します。
無限降下法は整数問題で時々出題されることがあります(東大2006年前期理科第4問などが有名です)。
