数Ⅲ微積で厄介者扱いされることの多い不定積分 $\displaystyle \int \sqrt{x^2+1}\,dx$ の図形的な導出法を紹介します。さらに、この不定積分を計算する際に用いられる $x+\sqrt{x^{2}+1}=t$ という置き換えの意味について考察します。
問題意識の背景
不定積分 $\displaystyle \int \sqrt{x^2+1}\,dx$ は普通、$$x+\sqrt{x^{2}+1}=t$$などという置換によって計算が進められます。他にも $x=\tan \theta$ と置いたり $x=\dfrac{e^{t}-e^{-t}}{2}$ などと置く方法もあるのですが、残念なことに多くの参考書や教科書ではこれらの置換を天下り的に用いており、そのモチベーションが明らかでないことがほとんどです。
【清史弘からの提案 7 】
教育系YouTuber の人に向けて、このような動画はどうですか? という内容です。もちろん、YouTuber でない方もご参加ください。
私の考え方は24時間以内にあげようと思っています。
これは、唯一の正解というよりは、いろいろとあってよいと思います。#清史弘からの提案 pic.twitter.com/UokREtslQt— 清 史弘 (@f_sei) September 13, 2020
このような置換積分を使わなければならないことの理由付けとして色々な説明が与えられていますが、結局はこの式が双曲線の式であるという事実が理解の根底にあります。その視点で考えれば、この不定積分の式は実は図形的に計算することが可能なのです。
置換 $x+\sqrt{x^{2}+1}=t$ の根拠については後で述べるとして、まずは不定積分 $\displaystyle \int \sqrt{x^2+1}\,dx$ を(ほぼ)図形的に導出する方法について紹介します。
曲線を回転する
$y=\sqrt{x^2+1}$ という関数を考えてみます。このグラフは以下のような双曲線になります。($y$軸との交点は$(0,\,1)$です)
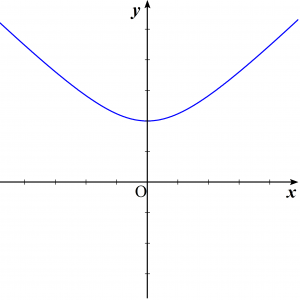
例えば定積分 $\displaystyle \int^{t}_{0} \sqrt{x^2+1}\,dx$ の値は以下の赤斜線部の面積に等しく、$$\dfrac{1}{2} \log \left(\sqrt{t^{2}+1}+t\right)+\dfrac{1}{2} t \sqrt{t^{2}+1}$$で与えられます。

このままでは考えにくいのでこれを$45^{\circ}$だけ時計回りに回転してみます。

計算すれば分かりますが、元の青色の曲線 $y=\sqrt{x^2+1}$ は陰関数表示にすると$$x^2-y^2=-1 \quad (x>0)$$と書けます。これを$45^{\circ}$だけ時計回りに回転したもの(赤色曲線)は$$xy=\dfrac{1}{2} \quad (x>0)$$となります(複素数などを使って確かめてみて下さい)。
こうすることで関数 $y=\dfrac{1}{2x}$ の積分を利用できるようになり、計算は格段にシンプルになります。
面積計算
以下のように各点を設定します。このとき、求める赤斜線部の面積を$S$とすると$$\small S=\triangle \mathrm{OAB}+\triangle \mathrm{OCD}+\text{図形}\mathrm{ABEF}-\triangle \mathrm{DEF}$$となります。
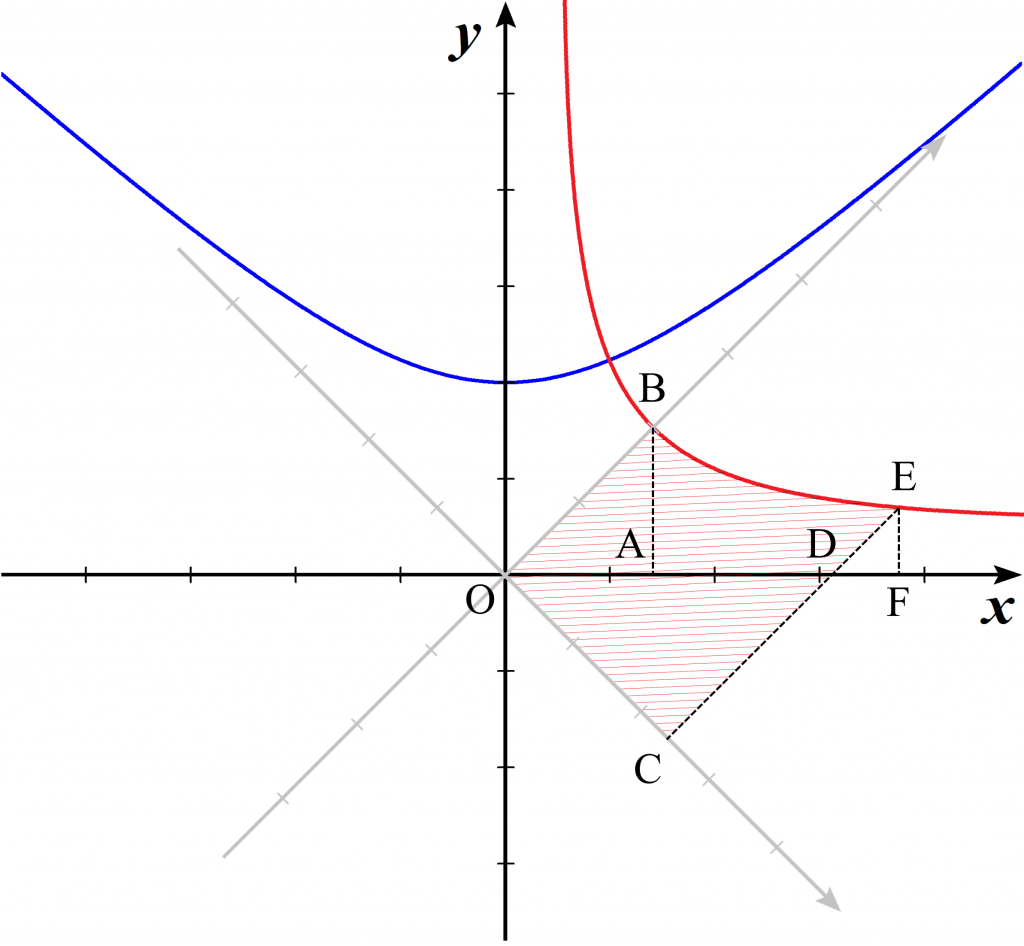
上の図において、回転前の座標軸は灰色で示しています。
$\triangle \mathrm{OAB}$ は $\mathrm{OB}=1$ の直角二等辺三角形なので $\mathrm{OA}=\mathrm{AB}=\dfrac{1}{\sqrt{2}}$ であり、$\triangle \mathrm{OCD}$ は $\mathrm{OC}=\mathrm{CD}=t$ の直角二等辺三角形なので、$\mathrm{OD}=\sqrt{2}\,t$ となります。
回転前の座標を考えれば $\mathrm{CE}=\sqrt{t^2+1}$ と表せるので、$$\mathrm{DE}=\sqrt{t^2+1}-t$$ $$\mathrm{DF}=\mathrm{EF}=\dfrac{\sqrt{t^2+1}-t}{\sqrt{2}}$$となり、$$\mathrm{OF}=\mathrm{OD}+\mathrm{DF}=\dfrac{\sqrt{t^2+1}+t}{\sqrt{2}}$$と表せます。
各線分の長さが出揃ったので、それぞれの図形の面積を求めることができます。
$\triangle \mathrm{OAB}=\dfrac{1}{2}\left(\dfrac{1}{\sqrt{2}}\right)^{2}=\dfrac{1}{4}$
$\triangle \mathrm{OCD}=\dfrac{1}{2} t^{2}$
$\text{図形}\mathrm{ABEF}=\displaystyle \int_{\frac{1}{\sqrt{2}}}^{\frac{\sqrt{t^{2}+1}+t}{\sqrt{2}}} \dfrac{1}{2 x} dx$
$\begin{align} \triangle \mathrm{DEF}&=\dfrac{1}{2}\left(\dfrac{\sqrt{t^{2}+1}-t}{\sqrt{2}}\right)^{2} \\ &=\dfrac{1}{2} t^{2}-\dfrac{1}{2} t \sqrt{t^{2}+1}+\dfrac{1}{4} \end{align}$
ここで$$\begin{align}
& \quad \displaystyle \int_{\frac{1}{\sqrt{2}}}^{\frac{\sqrt{t^{2}+1}+t}{\sqrt{2}}} \dfrac{1}{2 x} d x \\ &=\dfrac{1}{2}[\log x]_{\frac{1}{\sqrt{2}}}^{\frac{\sqrt{t^{2}+1}+t}{\sqrt{2}}} \\
&=\dfrac{1}{2}\left(\log \dfrac{\sqrt{t^{2}+1}+t}{\sqrt{2}}-\log \dfrac{1}{\sqrt{2}}\right) \\
&=\dfrac{1}{2}\left\{\log \left(\sqrt{t^{2}+1}+t\right)-\log \sqrt{2}+\log \sqrt{2}\right\} \\
&=\dfrac{1}{2} \log \left(\sqrt{t^{2}+1}+t\right)
\end{align}$$となるので、$$\small \begin{align}
S&=\triangle \mathrm{OAB}+\triangle \mathrm{OCD}+\text{図形}\mathrm{ABEF}-\triangle \mathrm{DEF} \\
&=\dfrac{1}{4}+\dfrac{1}{2} t^{2}+\dfrac{1}{2} \log \left(\sqrt{t^{2}+1}+t\right)-\left\{\dfrac{1}{2} t^{2}-\dfrac{1}{2} t \sqrt{t^{2}+1}+\dfrac{1}{4}\right\} \\
&=\dfrac{1}{2} \log \left(\sqrt{t^{2}+1}+t\right)+\dfrac{1}{2} t \sqrt{t^{2}+1}
\end{align}$$と求められます。これこそが求めるべき不定積分の式です。
以上より$$\small \displaystyle \int \sqrt{x^2+1}\,dx=\color{red}{\dfrac{1}{2} \log \left(\sqrt{t^{2}+1}+t\right)+\dfrac{1}{2} t \sqrt{t^{2}+1}+C}$$となることが(一部$\log$の積分を使いましたが)図形的に示すことができました。
$\small t=\sqrt{x^2+1}+x$ の意味
以上、不定積分 $\displaystyle \int \sqrt{x^2+1}\,dx$ の式は図形的に導出可能であることを示しました。それでは $t=\sqrt{x^2+1}+x$ という置き換えは何が根拠になっているのでしょうか?
まず、$y=\sqrt{x^2+1}$ は直角双曲線であり、その漸近線は $y=\pm x$(下図の緑色直線)です。
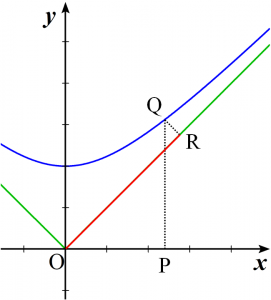
$\mathrm{OP}=x$ とすると$$\mathrm{PQ}=\sqrt{x^2+1}$$ $$\mathrm{OR}=\dfrac{\color{red}{\sqrt{x^2+1}+x}}{\sqrt{2}}$$となります。
これは係数を無視すれば、$\sqrt{x^2+1}+x$ という値が漸近線 $y=x$ を新たな軸に取り直したときの点$\mathrm{Q}$の座標成分になることを意味します。つまり、$t=\sqrt{x^2+1}+x$ という置き換えは座標軸の変換に対応していたのです($y=x$ を$t$軸に取り直して $\mathrm{OR}=\dfrac{1}{\sqrt{2}}t$ と置くイメージ)。
直角双曲線は $y=\sqrt{x^2+1}$ という形のまま扱うよりも $xy=\dfrac{1}{2}$ として扱う方が遥かに簡単です。実際に、煩雑な積分計算の一切を避けられることを前段で確認しました。つまり、$t=\sqrt{x^2+1}+x$ と置換すれば直角双曲線の漸近線を軸に取り直せるため、面積計算を単純化することができるのです。以上のことはこの置換の根拠と言って差し支えないでしょう。
(コメント)
$t=\sqrt{x^2+1}+x$ という置き換えは、実は座標軸を回転させれば自然に(?)導かれる置き換えだったのです。以上のことを踏まえれば、係数の付いた $\sqrt{ax^2+b}$ の不定積分であっても、座標系の相似拡大を考えることで自由自在に計算可能です。こんなことは教科書のどこにも書いておらず、とても面白い視点だと思います。
