前回に続いて「相似」に関連する平面図形の問題を紹介します。今回はやや大学受験生向けの内容です。
相似比を使って図形の計量を行うのは、何も中学生だけの領分ではありません。大学受験生は数学Ⅰ・Aで三角比やより高度な平面図形の知識を学ぶためか、相似な図形が全く見えなくなってしまうことがあります。「盲点」というやつですね。
大学受験生だからといって余弦定理を駆使してゴリゴリ計算するのが最善手とは言えません。相似な図形を見抜くことができれば計算量が抑えられ、それだけケアレスミスの確率も低くなります。という訳で、今回は相似な図形が隠れている大学入試問題を取り上げていきます。
大学入試から①
2013年のセンター試験で出題された図形問題です。受験界隈では悪い意味で(?)有名です。
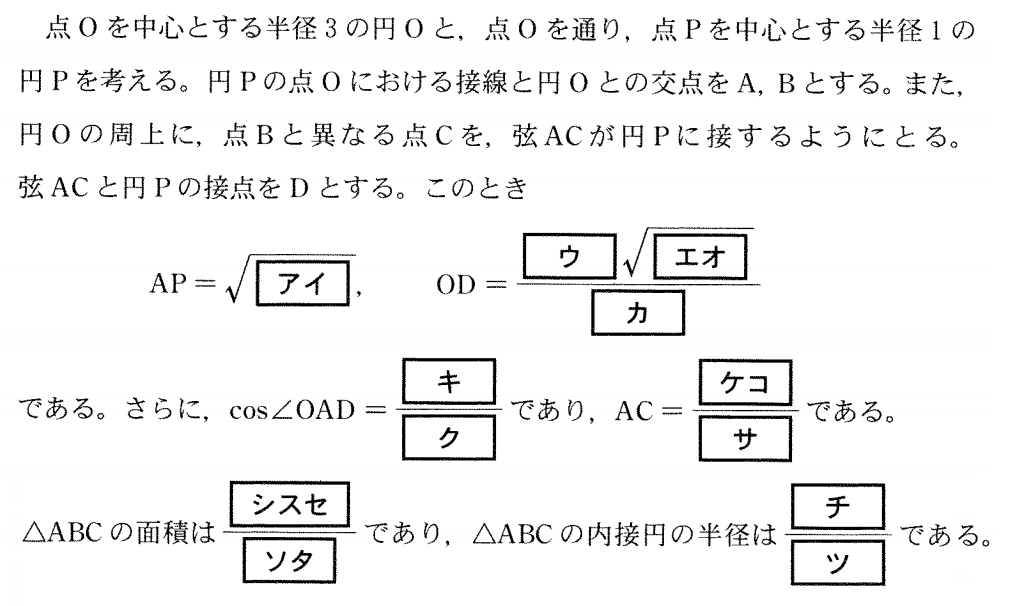 (出典:センター試験2013年数学Ⅰ・A第3問)
(出典:センター試験2013年数学Ⅰ・A第3問)
さて、問題文の条件をもとに図を描いてみると以下のようになります。
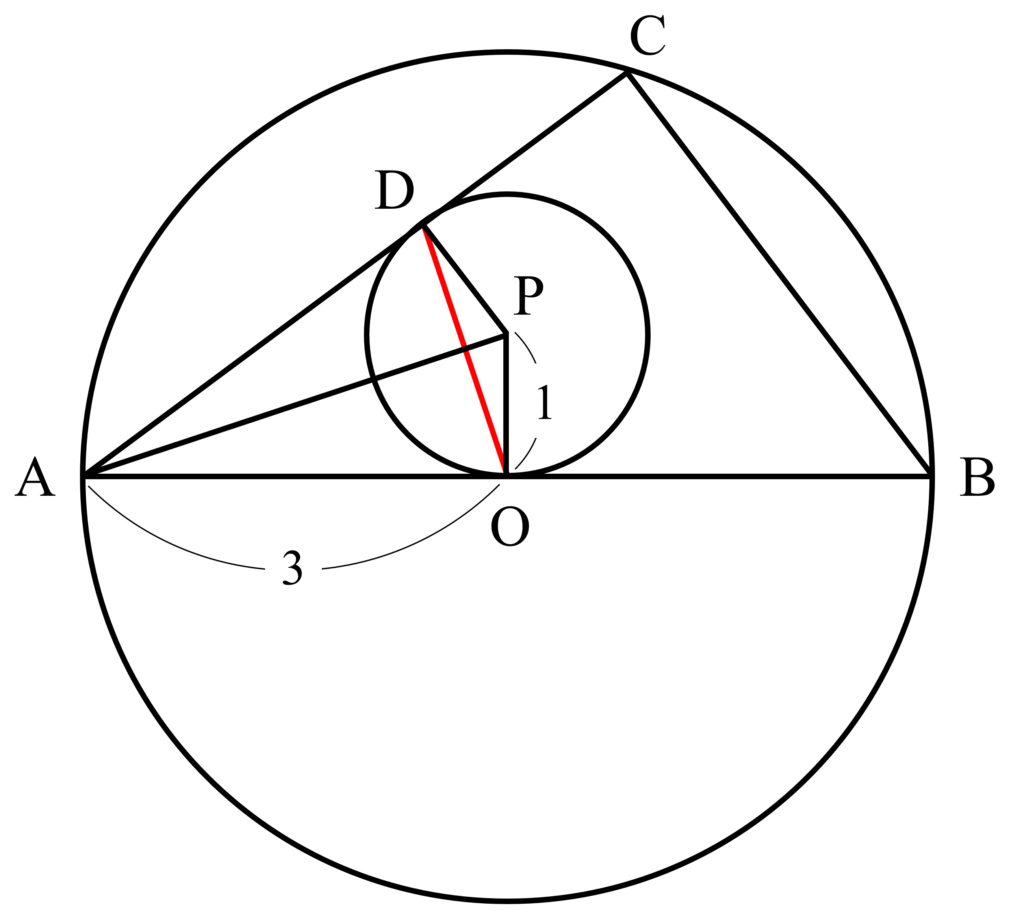
何の変哲もない図形問題なのですが、受験生の多くは$\mathrm{OD}$の導出で詰まってしまったそうです。皆さんはすぐに求められますよね・・・?(まずは自力で取り組んでみましょう)
» $\mathrm{OD}$の導出方法
($\mathrm{OD}$の導出方法)
下図のように相似な直角三角形を抜き出して考えます。$\mathrm{AP}=\sqrt{10}$ は三平方の定理からすぐに求められます。

図に示した三角形の相似比より $\dfrac{1}{2}\mathrm{OD}=\dfrac{3}{\sqrt{10}}$ と求められるので、$$\mathrm{OD}=\color{red}{\dfrac{3\sqrt{10}}{5}}$$を得ます。
もしくは、$\triangle \mathrm{OPA}$が直角三角形であることから $\sin\angle \mathrm{OPA}=\dfrac{3}{\sqrt{10}}$ が直ちに分かるので、$\dfrac{1}{2}\mathrm{OD}=\mathrm{OP}\sin\angle \mathrm{OPA}$ として求めることもできます。これは実質的に相似を用いた方法と同じです。
ここまで悩む余地など皆無なのですが、多くの大学受験生は三角形の相似などとうの昔に忘れ去っていたらしく、アとイのマークしか埋められなかった人が続出したとか・・・。この年の数学Ⅰ・A第4問の確率もクセのある問題だったためか、この年の数Ⅰ・Aの平均点は51.20点と歴代ワースト3位の低さを記録しました。
本問に関しては、その後の設問で$\mathrm{OD}$の長さを使う(ように見える)ので焦りが焦りを呼び、出来はかなり悲惨だったようです(実際には$\cos \angle \mathrm{OAD}$の値は2倍角の公式からも導出可能)。こうした事態に陥らないためにも、相似の考え方は頭の片隅に常に置いておくべきでしょう。試験本番で柔軟な視点が持てるかどうかは日頃の訓練のやり方に依るところ大です。
最も遠回りな方法は、$\triangle \mathrm{OPA}$から$\cos\angle \mathrm{OPA}$を求め、二倍角の公式から$\cos\angle \mathrm{OPD}$を求めて$\triangle \mathrm{OPD}$について余弦定理を用いる方法でしょうか。余弦定理まで持ち出さなくても直角三角形になっているのだから三角比を使えばいいのに・・・、という気持ちになりますが。
誘導を無視すれば、方べきの定理の利用も考えられそうですが、$\mathrm{OA}$の長さの情報を利用できないので未知数が残ってしまいます。やはり相似比から直ちに求めてしまうのが速いですね。
» 閉じる
大学入試から②
平行四辺形$\mathrm{ABCD}$において、辺$\mathrm{AB}$を$1:1$に内分する点を$\mathrm{E}$、辺$\mathrm{BC}$を$2:1$に内分する点を$\mathrm{F}$、辺$\mathrm{CD}$を$3:1$に内分する点を$\mathrm{G}$とする。線分$\mathrm{CE}$と線分$\mathrm{FG}$の交点を$\mathrm{P}$とし、線分$\mathrm{AP}$を延長した直線と辺$\mathrm{BC}$の交点を$\mathrm{Q}$とするとき、比$\mathrm{AP}:\mathrm{PQ}$を求めよ。
(2013年京都大学前期共通 理系第1問/文系第2問)
2013年の京都大学で出題された図形問題です。ベクトルを使いたくなりますが、もっと上手い方法はないでしょうか?
まずは15分程度を目安に、自力で解いてみて下さい。京大の数学としては異様に易しい問題です。
» 解答の流れ
(解答の流れ)
ベクトルによる解法は省略。補助線を引いて幾何のみで攻めます。

図のように点$\mathrm{H}$、$\mathrm{I}$をとります。$\mathrm{DI}=x$ と置くと、$\triangle \mathrm{GDI} \sim \triangle \mathrm{GCF}$ より $\mathrm{CF}=3x$ となるので $\mathrm{AD}=\mathrm{BC}=9x$ です。また、$\triangle \mathrm{ECB} \equiv \triangle \mathrm{EHA}$ より $\mathrm{AH}=9x$ となるので、$\mathrm{HI}=19x$ です。
ここで、$\triangle \mathrm{PQF} \sim \triangle \mathrm{PAI}$ および $\triangle \mathrm{PCF} \sim \triangle \mathrm{PHI}$ より、$$\mathrm{AP}:\mathrm{PQ}=\mathrm{IP}:\mathrm{PF}=\mathrm{HI}:\mathrm{CF}$$となるので$$\mathrm{AP}:\mathrm{PQ}=\color{red}{19:3}$$と求められます。
補助線を引く分、広い視野が必要ですが、ベクトルを使うよりも遥かに簡単に解決できます。
» 閉じる
大学入試から③
京大からもう1題、2010年に出題された図形問題を取り上げます。「正十角形」に惑わされないように。
点$\mathrm{O}$を中心とする正十角形において、$\mathrm{A}$、$\mathrm{B}$を隣接する2つの頂点とする。線分$\mathrm{OB}$上に $\mathrm{OP}^2=\mathrm{OB} \cdot \mathrm{PB}$ を満たす点$\mathrm{P}$をとるとき、$\mathrm{OP}=\mathrm{AB}$ が成立することを示せ。
(2010年京都大学前期文系 第4問)
正十角形は以下のようになりますがこの図を丁寧に描く必要は無く、$\triangle \mathrm{OAB}$ の部分のみを考えれば十分です。
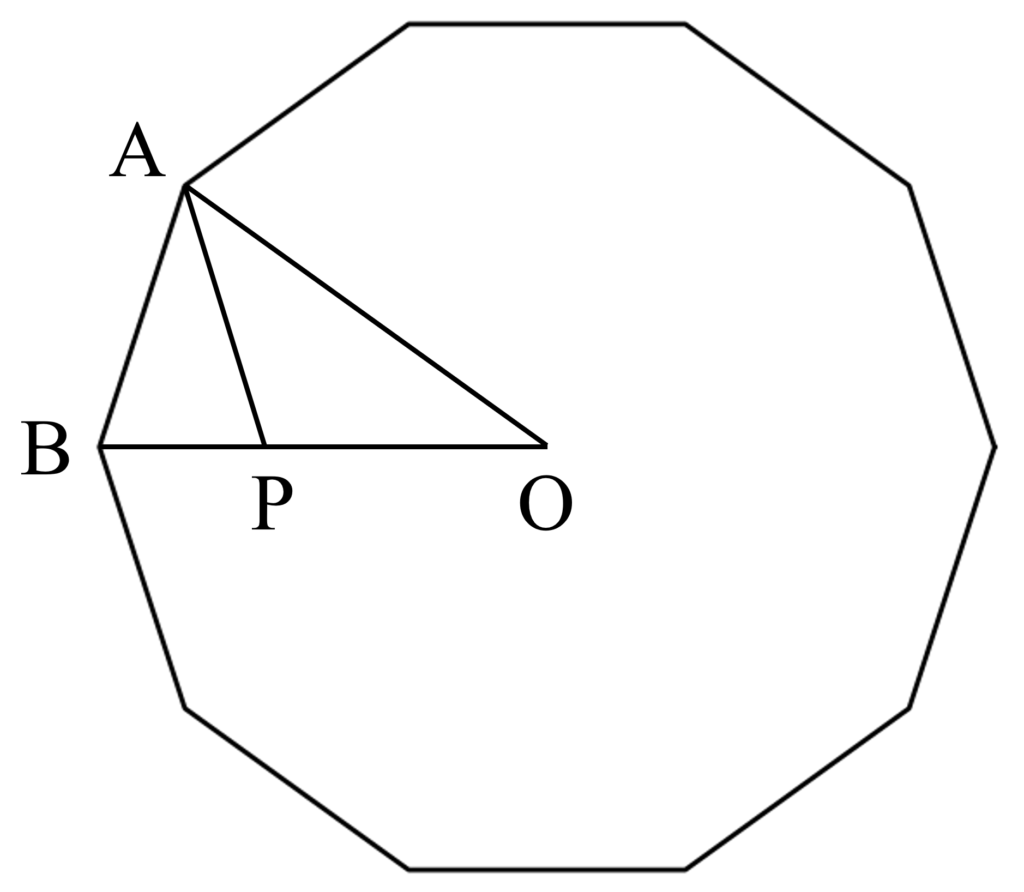
» 解答の流れ
(解答の流れ)
まず、題意の命題は一般の正十角形について成り立つことを主張するものなので、半径$1$の円に内接する正十角形を考えれば十分です。
仮定より、$$\mathrm{OP}^2=\mathrm{OB} \cdot \mathrm{PB}$$ $$\therefore \mathrm{OP}^2=1 \cdot (1-\mathrm{OP})$$ $$\therefore \mathrm{OP}^2+\mathrm{OP}-1=0$$となるので、これを$\mathrm{OP}$について解いて$$\mathrm{OP}=\dfrac{\sqrt{5}-1}{2} \ (>0)$$を得ます。よって$$\begin{align} \mathrm{BP}:\mathrm{OP} &=\dfrac{3-\sqrt{5}}{2}:\dfrac{\sqrt{5}-1}{2} \\ &= \dfrac{3-\sqrt{5}}{\sqrt{5}-1}:1 \\ &= \dfrac{\sqrt{5}-1}{2}:1 \end{align}$$となるので、線分$\mathrm{AP}$は$\mathrm{BO}$を $\dfrac{\sqrt{5}-1}{2}:1$ に内分します。
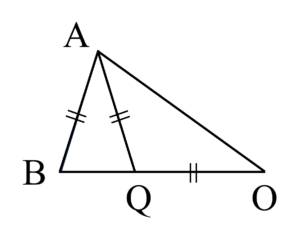
ここで、上図のように二等辺三角形$\mathrm{OAB}$について $\mathrm{AB}=\mathrm{AQ}$ となるような点$\mathrm{Q}$を辺$\mathrm{OB}$上にとります。このような点$\mathrm{Q}$は辺$\mathrm{OB}$上にただ1点だけ存在することに注意して下さい。
$\triangle \mathrm{OAB}$と$\triangle \mathrm{ABQ}$は底角の等しい二等辺三角形なので$$\triangle \mathrm{OAB} \sim \triangle \mathrm{ABQ}$$であり、$\angle \mathrm{AOB}=\angle \mathrm{BAQ}=36^{\circ}$ より、$\triangle \mathrm{QOA}$は $\mathrm{QA}=\mathrm{QO}$ の二等辺三角形と分かります。よって$$\mathrm{AB}=\mathrm{QA}=\mathrm{OQ} \quad \cdots (*)$$が成立します。
また、このとき$\mathrm{AQ}$は$\angle \mathrm{OAB}$の二等分線なので$\mathrm{BO}$を$\mathrm{AB}:\mathrm{AO}$に内分します。$\triangle \mathrm{OAB}$と$\triangle \mathrm{ABQ}$は相似なので$$\mathrm{AB}:\mathrm{AO}=\mathrm{BQ}:\mathrm{AB}$$ $$\therefore \mathrm{AB}^2=1 \cdot (1-\mathrm{OQ})$$ $$\therefore \mathrm{AB}^2=(1-\mathrm{AB}) \quad (\because (*))$$となります。この解は先ほどの$\mathrm{OP}$の2次方程式と同様に$\mathrm{AB}=\dfrac{\sqrt{5}-1}{2}$ と求められ、これより $\mathrm{AB}:\mathrm{AO}=\dfrac{\sqrt{5}-1}{2}:1$ となります。
よって $\mathrm{BP}:\mathrm{OP}=\mathrm{AB}:\mathrm{AO}$ となるから線分$\mathrm{AP}$は$\angle \mathrm{OAB}$の二等分線であり、点$\mathrm{P}$は点$\mathrm{Q}$に一致するから$(*)$より $\mathrm{OP}=\mathrm{AB}$ が成立します。以上の議論は、辺の長さを定数倍することで任意の辺の長さの正十角形について適用できるので、これで題意の命題が示されました。
あるいは以下のような証明方法もあります。
$\triangle \mathrm{OAB}$について$\angle \mathrm{OAB}$の二等分線$\mathrm{AQ}$を引き、$\angle \mathrm{OAB}=2\theta$ と置きます。
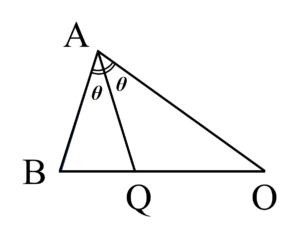
$\triangle \mathrm{OAB}$は二等辺三角形なので$$\angle \mathrm{OAB}=\angle \mathrm{OBA}=2\theta$$であり、$$\angle \mathrm{AOB}=\pi-4\theta$$です。正十角形の中心角$\angle \mathrm{AOB}$は $\dfrac{2\pi}{10}$ なので、$$\theta=\dfrac{\pi}{5}\ (=36^{\circ})$$と求められます。よって $\angle \mathrm{QAO}=\angle\mathrm{QOA}=\theta$ より、$\triangle \mathrm{OAQ}$は $\mathrm{QA}=\mathrm{QO}$ の二等辺三角形と分かります。また、$\angle \mathrm{BQA}$は$\angle \mathrm{OQA}$の外角なので$$\begin{align} \angle \mathrm{BQA}&=\angle \mathrm{QAO}+\angle \mathrm{QOA} \\ &=\theta+\theta \\ &=2\theta \\ &=\angle \mathrm{QBA} \end{align}$$となり、これと $\mathrm{OBA}=2\theta$ であることから$\triangle \mathrm{ABQ}$が二等辺三角形であることが従います。
以上より、$$\mathrm{OQ}=\mathrm{AQ}=\mathrm{AB} \quad \cdots (*)$$が成り立ちます。
また、角の二等分線の性質から、$$\mathrm{AB}:\mathrm{AO}=\mathrm{QB}:\mathrm{OQ}$$が成り立ちます。ここで、$\mathrm{AB}=\mathrm{OQ}$、$\mathrm{AO}=\mathrm{OB}$ より、$$\mathrm{OQ}:\mathrm{OB}=\mathrm{QB}:\mathrm{OQ}$$ $$\therefore \mathrm{OQ}^2=\mathrm{OB}\cdot\mathrm{QB}$$を得ます。
ところで、図より $\mathrm{OP}^2=\mathrm{OB} \cdot \mathrm{PB}$ を満たすような線分$\mathrm{OB}$上の点$\mathrm{P}$はただ一つしか存在しないから、点$\mathrm{P}$は点$\mathrm{Q}$と同一の点です。
したがって、$(*)$より$$\mathrm{OP}=\mathrm{AB}$$が成り立ちます。
□
頂角が$36^{\circ}$の二等辺三角形は頻出です。相似な図形が見抜ければ $\dfrac{\pi}{5}$ の三角比だって怖くありません。
» 閉じる

相似な図形は色々な所に潜んでいます。大学入試問題の勉強をしていると解法の選択肢が多くなるせいか、なかなか初等幾何の発想が浮かばないものです。いざという時に「盲点」に遭遇しないためにも、日頃からパターンに囚われない柔軟な思考力を鍛えておきたいですね。
ところで、数学についての理解力や知識はあるのに成績が伸び悩んでいるという人は、自分の解き方に固執しすぎているかもしれません。一つの問題に対して色々な解法が存在することは皆さん理解していると思いますが、「解ければいいや」で済ませているといつまでたっても成績は伸びません。身に覚えはありませんか?
様々な別解の考え方を吸収して、解法の引き出しをできるだけ沢山増やしてください。数学に限った話ではありませんが、勉強で一番大切なのは問題を解いているときではなく、答案を自己採点して具体的に反省し、さらに別解までを自分の血肉にするべく学んでいるときです。視野が広がると今度は学ぶことが楽しくなるはずです。