曲線の長さの導出は立体の積分と並んで数Ⅲで学ぶ解析分野の最高峰として難関大の入試で頻出のテーマです。今回は放物線の曲線の長さを解析的に求めてみます。
曲線の長さの公式
曲線の長さを求める公式について復習しておきましょう。弧長積分の公式とは以下のようなものでした。
媒介変数表示された関数の弧長
$f$、$g$ が連続かつ微分可能で $f^{\prime}$、$g^{\prime}$も連続とするとき、$\begin{cases}x=f(t) \\ y=g(t) \end{cases}$ と媒介変数表示された曲線の $\alpha\leqq t\leqq \beta$ の部分の長さは、$$\displaystyle\int_{\alpha}^{\beta}\sqrt{f'(t)^2+g'(t)^2}dt$$によって与えられる。
この公式は曲線の長さを無限小の折れ線によって近似して得られます。以下の図において $n \to \infty$ とすれば折れ線の長さの総和は曲線の長さに等しくなります(詳しい証明は教科書に載っていますので、ここでは省略します)。
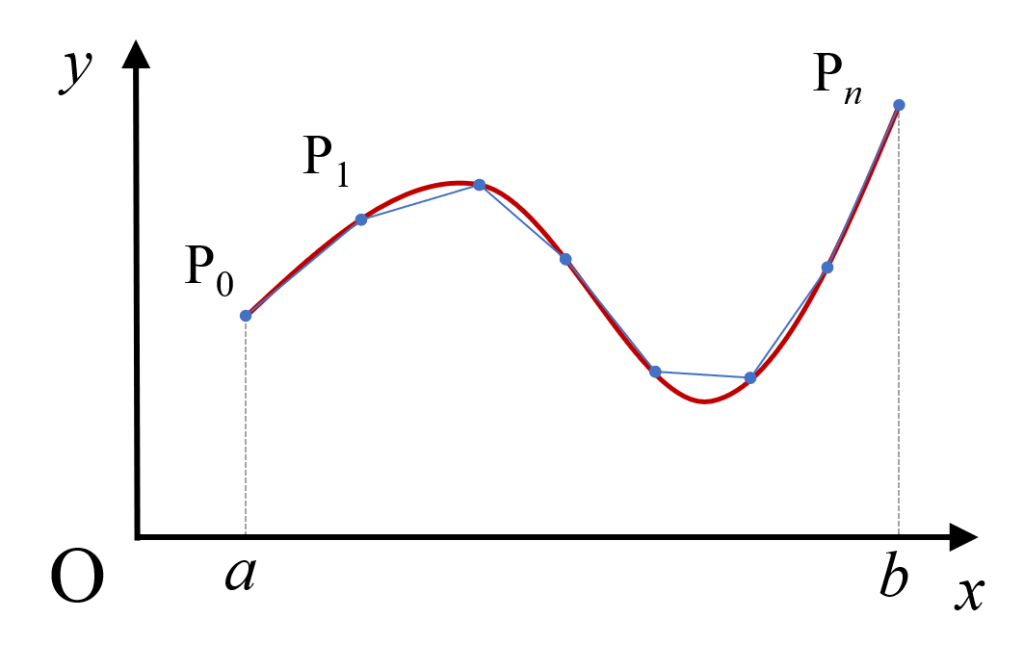
陽関数の場合はこの媒介変数$t$を$x$とすればよく、$\dfrac{dx}{dt} \to \dfrac{dx}{dx}=1$、$\dfrac{dy}{dt} \to \dfrac{dy}{dx}$、$dt \to dx$ の置き換えにより以下の公式を得ます。
陽関数の弧長
$f$ が連続かつ微分可能で $f^{\prime}$ も連続とするとき、曲線 $y=f(x)$ の $a \leqq x \leqq b$ の部分の長さは、$$\displaystyle\int_{a}^{b}\sqrt{1+f'(x)^2}dx$$によって与えられる。
放物線は陽関数として表示可能なので、今回はこちらの公式を利用します。
放物線の長さを求めよう
早速、放物線 $y=px^2$ の長さを求めてみましょう($p$は正の実数)。放物線は頂点を通る軸に関して線対称なので $x \geqq 0$ の部分を考えれば十分です。
上記の公式により $0 \leqq x \leqq a$ の部分の長さ$L_{p,a}$は、$$\begin{align} L_{p,a} &= \int_{0}^{a}\sqrt{1+f'(x)^2}dx \\ &= \int_{0}^{a}\sqrt{1+4p^2 x^2}dx \end{align}$$となります。ここで、$t=2px$ と置けばこの積分は$$\displaystyle \dfrac{1}{2p}\int_{0}^{2pa}\sqrt{1+t^2}dt$$と変換されるので、不定積分$$\int\sqrt{1+t^2}dt$$が求められれば一般の場合に適用できます。
ここで次の公式*1の出番です。$$\int\sqrt{x^2+1}\,dx =\dfrac{1}{2}x\sqrt{x^2+1}+\dfrac{1}{2}\log(\sqrt{x^2+1}+x)+C$$この公式を用いると$$L_{p,a}=\displaystyle \dfrac{1}{2p}\left\{pa\sqrt{4p^2 a^2+1}+\dfrac{1}{2}\log\left(\sqrt{4p^2 a^2+1}+2pa\right)\right\}$$と求められます。
これより、$p=1$ の場合、すなわち $y=x^2$ の $0 \leqq x \leqq 1$ の部分の長さ$L_{1,1}$は$$\displaystyle \dfrac{\sqrt{5}}{2}+\dfrac{1}{4}\log\left(\sqrt{5}+2\right)$$と求められます。
また、$y=2x^2$ の $1 \leqq x \leqq 2$ の部分の長さは $L_{2,2}-L_{2,1}$ となるので$$\sqrt{65}-\dfrac{\sqrt{17}}{2}+\dfrac{1}{8}\left\{\log\left(\sqrt{65}+8\right)-\left(\sqrt{17}+4\right)\right\}$$と求められます。
入試で頻出の関数
放物線の弧長は式の見た目が煩雑なので計算ミスに注意です。入試でよく出るタイプの関数としては放物線の他に、
カテナリー
$$f(x)=\dfrac{e^{x}+e^{-x}}{2}$$
対数関数
$$f(x)=\log x$$
次数が半整数の関数
$$f(x)=x^{\frac{3}{2}}$$
などがあります。$y=\sqrt {r^2 – x^2}$ を用いて半径$r$の円周が$2\pi r$となることを示すこともできます。入試問題ではありませんが、「鉄塔の間隔は何m?」~Amazon入社試験よりのページでカテナリーについて触れています。
*1 $\displaystyle\int\sqrt{x^2+1}\,dx$ の積分について
この公式は $\cos$ 関数による置換積分などを駆使して導出することができます。以下のように不定積分の結果(右辺)を微分してみると正しいことが確かめられます。
$\begin{align}(x \sqrt{x^{2}+1})^{\prime} &=\sqrt{x^{2}+1}+\frac{x^{2}}{\sqrt{x^{2}+1}} \\ &=\sqrt{x^{2}+1}+\sqrt{x^{2}+1}-\frac{1}{\sqrt{x^{2}+1}} \\ &=2 \sqrt{x^{2}+1}-\frac{1}{\sqrt{x^{2}+1}} \end{align}$
$\begin{align}(\log (x+\sqrt{1+x^{2}}))^{\prime} &=\frac{1+x / \sqrt{1+x^{2}}}{x+\sqrt{1+x^{2}}} \\ &=\frac{1}{\sqrt{1+x^{2}}} \end{align}$

“【曲線の長さの公式】放物線の長さを求めてみよう” への1件の返信