前回解説した「ニュートン法」を用いて曲面上における停留点を探索してみます。今回はその一つである「鞍点」について詳しく考察してみます。化学寄りの話題も含みます。
目次
・ニュートン法は停留点へ向かう
・3種類の停留点
・ニュートン法で停留点を探そう!
・ヘッセ行列の固有値と固有ベクトル
・停留点チャレンジ
(Himmelblau’s functionを例に)
・まとめ
ニュートン法は停留点へ向かう
ニュートン法は2次関数で目的関数の近似し、その極小点方向に座標を更新していくという最適化手法でした。しかしニュートン法が必ずしも目的関数の値を最小化する訳ではないことに注意する必要があります。
そもそもニュートン法がどのようなアルゴリズムで座標を更新してるかを確認しておく必要があります。前回の記事の「ニュートン法のコンセプト」の項を参考にしてください。
ニュートン法は目的関数の2次近似によって最適化を行う手法で、目的関数の1次微分、すなわち勾配がゼロになる点に向かって座標を更新していきます。つまり、ニュートン法で最終的に辿り着く点は「勾配がゼロである点」であって、必ずしも極小点とは限りません。
3種類の停留点
勾配(1次微分)の値がゼロとなる点を「停留点」と呼びます。停留点には以下の3種類があります。
・ 極大点
・ 極小点
・ 鞍点
イメージとしては「平らになっている点」が停留点に相当します。
2変数関数$$f(x_1,x_2)=\dfrac{1}{2}\sin x_1-\cos x_2$$を例に図示すると以下のようになります。
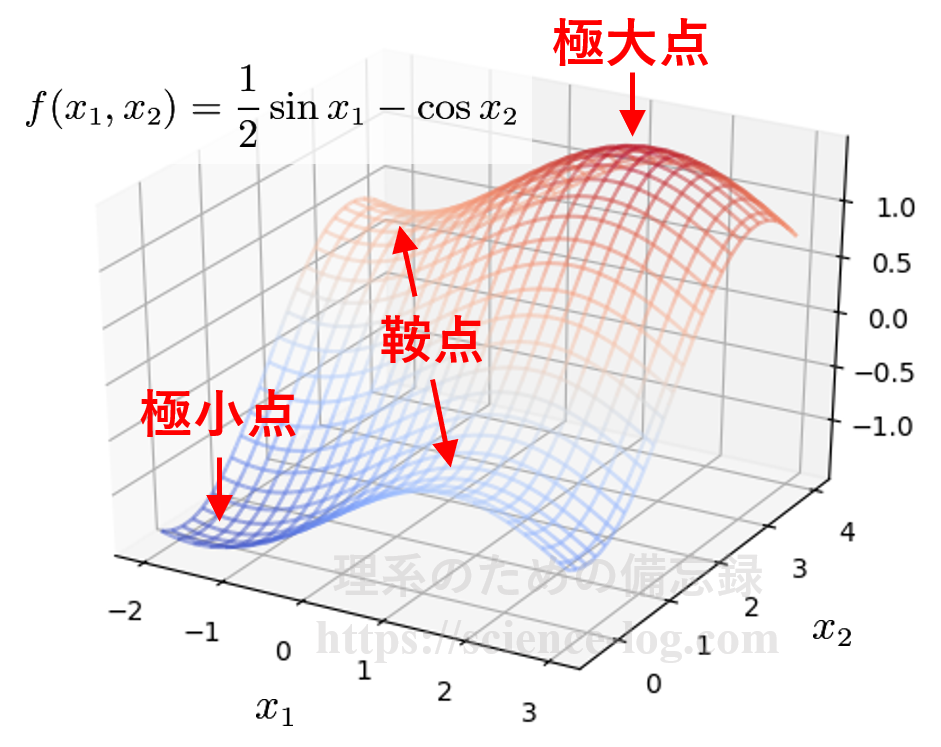
※上図は $-2.0 \leqq x_1 \leqq 3.0$、$-0.4 \leqq x_2 \leqq 4.0$ の範囲のみ図示しています。この$f(x_1,x_2)$は周期関数なので極大点、極小点、鞍点は無数に存在します。
図示した範囲に存在する停留点は4つ存在します。
● 極大点:$\left(\dfrac{\pi}{2},\,\pi\right)$
● 極小点:$\left(-\dfrac{\pi}{2},\,0\right)$
● 鞍点 :$\left(-\dfrac{\pi}{2},\,\dfrac{\pi}{2}\right)$、$\left(\dfrac{\pi}{2},\,0\right)$
これらの点が停留点になっていることは偏導関数により確かめることができます。ある点が停留点であるための必要十分条件は、すべての第1次偏導関数の値がゼロであることです。
ここで、$\small f(x_1,x_2)=\dfrac{1}{2}\sin x_1-\cos x_2$ の第1次偏導関数は$$\begin{cases} \dfrac{\partial f}{\partial x_1}=\dfrac{1}{2}\cos x_1 \\ \dfrac{\partial f}{\partial x_2}=\sin x_2 \end{cases}$$となり、第2次偏導関数は
$$\begin{cases} \dfrac{\partial^2 f}{\partial x_1^2}=-\dfrac{1}{2}\sin x_1 \\ \dfrac{\partial^2 f}{\partial x_1 x_2}=0 \\ \dfrac{\partial^2 f}{\partial x_2^2}=\cos x_2 \end{cases}$$となります。
したがって、停留点では$$\begin{cases} \dfrac{1}{2}\cos x_1=0 \\ \sin x_2=0 \end{cases}$$より、$$x_1=\pi n_{1}-\dfrac{\pi}{2}, \ x_2=\pi n_{2}, \quad n_{1} \in \mathbb{Z}, \ n_{2} \in \mathbb{Z}$$を満たしています。
ニュートン法で停留点を探そう!
$-2.0 \leqq x_1 \leqq 3.0$、$-0.4 \leqq x_2 \leqq 4.0$ の範囲に存在する$$f(x_1,x_2)=\dfrac{1}{2}\sin x_1-\cos x_2$$の停留点をニュートン法で求めてみましょう。コードの実装例は以下のようになります。
import numpy as np
def f(x, y):
return np.sin(x)/2 - np.cos(y)
def fx(x, y):
h = 1e-7
return (f(x+h, y)-f(x-h, y))/(2*h)
def fy(x, y):
h = 1e-7
return (f(x, y+h)-f(x, y-h))/(2*h)
def fxx(x, y):
h = 1e-7
return (fx(x+h, y)-fx(x-h, y))/(2*h)
def fxy(x, y):
h = 1e-7
return (fx(x, y+h)-fx(x, y-h))/(2*h)
def fyy(x, y):
h = 1e-7
return (fy(x, y+h)-fy(x, y-h))/(2*h)
# input section
xc1 = 1.0; yc1 = 2.0 # 初期値
stepsize = 1 # ステップ幅
maxtimes = 10000 # 最大試行回数
times = maxtimes # 試行回数カウント用変数
# Newton-Raphson method ニュートン・ラフソン法
for i in range(1, maxtimes):
diffx1 = fx(xc1, yc1); diffy1 = fy(xc1, yc1)
if np.sqrt(diffx1 ** 2 + diffy1 ** 2) < 1e-7:
times = i
break
else:
det = fxx(xc1, yc1) * fyy(xc1, yc1) - fxy(xc1, yc1) ** 2
x_element = fx(xc1, yc1) * fyy(xc1, yc1) - fy(xc1, yc1) * fxy(xc1, yc1)
y_element = - fx(xc1, yc1) * fxy(xc1, yc1) + fxx(xc1, yc1) * fy(xc1, yc1)
xc2 = xc1 - stepsize * x_element / det # 次のx座標を生成
yc2 = yc1 - stepsize * y_element / det # 次のy座標を生成
xc1 = xc2; yc1 = yc2 # 座標の更新
# 試行回数
print("done! ( i =", times, ")")
# 極小点の座標
print("(", xc1, ",", yc1,")")
# 極小点での値と勾配の大きさ
print("z =", f(xc1, yc1), ", |d| =", np.sqrt(diffx1 ** 2 + diffy1 ** 2))
# ヘッセ行列
Hessian = np.array([[fxx(xc1, yc1),fxy(xc1, yc1)],[fxy(xc1, yc1),fyy(xc1, yc1)]])
# 固有値・固有ベクトルをそれぞれeig_val, eig_vecに格納
eig_val, eig_vec =np.linalg.eig(Hessian)
# 固有値
print(eig_val)
# 固有ベクトル
print(eig_vec)
※今回はmathモジュールではなく数値計算ライブラリであるnumpyをインポートしています。これは後述するヘッセ行列の固有値と固有ベクトルを計算するモジュールを利用するためです(一応、numpyを使わずにベタ書きしても実装可能です)。
初期値は $(\pm 1.0,\, \pm 2.0)$(複合任意)とするのが良いでしょう。先ほど挙げた4つの停留点が見つかるはずです。以下に出力結果をまとめたものを載せておきます。
# xc1 = 1.0; yc1 = 2.0 done! ( i = 7 ) ( 1.570796326345029 , 3.141592653008608 ) z = 1.5 , |d| = 1.1102230246251565e-09 [-0.49960036 -0.99920072] [[1. 0.] [0. 1.]] # xc1 = 1.0; yc1 = 0.0 done! ( i = 4 ) ( 1.5707963203899926 , 0.0 ) z = -0.5 , |d| = 3.3306690738754696e-09 [-0.49960036 0.99920072] [[1. 0.] [0. 1.]] # xc1 = -1.0; yc1 = 0.0 done! ( i = 5 ) ( -1.570796320194075 , 0.0 ) z = -1.5 , |d| = 3.3306690738754696e-09 [0.49960036 0.99920072] [[1. 0.] [0. 1.]] # xc1 = -1.0; yc1 = 2.0 done! ( i = 7 ) ( -1.5707963270771752 , 3.1415926517835135 ) z = 0.5 , |d| = 2.220446049250313e-09 [ 0.49960036 -0.99920072] [[1. 0.] [0. 1.]]
このプログラムでは、停留点の座標、$z=f(x_1,x_2)$ の値、勾配の絶対値、固有値、固有ベクトルを出力しています。全部見つけられましたか?
ヘッセ行列の固有値と固有ベクトル
「ヘッセ行列による多変数関数の極値判定」でも解説した通り、ヘッセ行列の首座小行列式の正負を調べることで停留点の極値判定が可能です。しかしここでは、鞍点について詳しく調べるためにヘッセ行列の固有値の正負を調べることにします。
一般に、2次の正方行列の固有値を求めるには、$$\begin{align} \mathbf{U}^{\dagger} \mathbf{O} \mathbf{U} &=\left[\begin{array}{ll}
U_{11} & U_{21} \\
U_{12} & U_{22}
\end{array}\right]\left[\begin{array}{ll}
O_{11} & O_{12} \\
O_{12} & O_{22}
\end{array}\right]\left[\begin{array}{ll}
U_{11} & U_{12} \\
U_{21} & U_{22}
\end{array}\right] \\
&=\left[\begin{array}{cc}
\omega_{1} & 0 \\
0 & \omega_{2}
\end{array}\right] \end{align}$$と対角化できるような2次のユニタリー行列$\mathbf{U}$を見つければよいことが知られています。
※ユニタリー行列とは関係式$$\mathbf{U}^{\dagger} \mathbf{U}=\mathbf{E}$$を満たす行列で、「等長写像」とも呼ばれます。ここで、$\mathbf{U}^{\dagger}$は行列$\mathbf{U}$の「随伴行列」を表し、$\mathbf{E}$は単位行列を表しています。
2次のユニタリー行列は、$$\begin{align} \mathbf{U}^{\dagger} \mathbf{U} &=\left[\begin{array}{ll}
U_{11} U_{11}+U_{21} U_{21} & U_{11} U_{12}+U_{21} U_{22} \\
U_{12} U_{11}+U_{22} U_{21} & U_{12} U_{12}+U_{22} U_{22}
\end{array}\right] \\
&=\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right] \end{align}$$という関係式を満たします。これより、4個の未知数に対して3本の等式が得られるため、2次のユニタリー行列はただ1つのパラメータを使って表せることが分かります。この2次のユニタリー行列はその性質上、一種の回転行列と見なすことができ、パラメーター$\theta$を用いて$$\mathbf{U}=\left[\begin{array}{lr}
\cos \theta & \sin \theta \\
\sin \theta & -\cos \theta
\end{array}\right]$$と表すことができます。このとき、2次の行列$\mathbf{O}$に対して$$\small \begin{aligned}
& \quad \mathbf{U}^{\dagger} \mathbf{O} \mathbf{U} \\
&=\left[\begin{array}{cc}
\cos \theta & \sin \theta \\
\sin \theta & -\cos \theta
\end{array}\right]\left[\begin{array}{ll}
O_{11} & O_{12} \\
O_{12} & O_{22}
\end{array}\right]\left[\begin{array}{ll}
\cos \theta & \sin \theta \\
\sin \theta & -\cos \theta
\end{array}\right] \\
&=\left[\begin{array}{cc}
O_{11} \cos ^{2} \theta+O_{22} \sin ^{2} \theta +O_{12} \sin 2 \theta & \dfrac{1}{2}\left(O_{11}-O_{22}\right) \sin 2 \theta-O_{12} \cos 2 \theta \\
\dfrac{1}{2}\left(O_{11}-O_{22}\right) \sin 2 \theta-O_{12}\cos 2 \theta & O_{11} \sin ^{2} \theta+O_{22} \cos ^{2} \theta-O_{12} \sin 2 \theta
\end{array}\right]
\end{aligned}$$となります。これが対角行列であるためには$$\dfrac{1}{2}\left(O_{11}-O_{22}\right) \sin 2 \theta-O_{12} \cos 2 \theta=0$$が成り立つことが必要で、この解を$\theta_{0}$とすれば$$\theta_{0}=\dfrac{1}{2} \tan ^{-1} \frac{2 O_{12}}{O_{11}-O_{22}}$$と表されます。これより、2つの固有値は$$\begin{cases}
\omega_{1}=O_{11} \cos ^{2} \theta_{0}+O_{22} \sin ^{2} \theta_{0}+O_{12} \sin 2 \theta_{0} \\
\omega_{2}=O_{11} \sin ^{2} \theta_{0}+O_{22} \cos ^{2} \theta_{0}-O_{12} \sin 2 \theta_{0}
\end{cases}$$と求められるので、2つの固有ベクトルは$$\begin{aligned}
\mathbf{v}_{1}&=\left[\begin{array}{l}
\cos \theta_{0} \\
\sin \theta_{0}
\end{array}\right] \\
\mathbf{v}_{2}&=\left[\begin{array}{r}
\sin \theta_{0} \\
-\cos \theta_{0}
\end{array}\right]
\end{aligned}$$で与えられます。上記のサンプルコードの「np.linalg.eig(Hessian)」の行では、2次のヘシアン$\mathbf{H}$に対してこれと同じことをやっています。以上の原理が分かっていればnumpyに頼らなくても実装は可能です。
今のケースで重要なのは固有値の正負です。2変数関数を考えているので、ヘッセ行列の固有値は2つだけ存在します。ある停留点における2つの固有値がいずれも負であればその点は極大点になっており、いずれも正であればその点は極小点になっています。2つの固有値の符号が異なる場合は鞍点に対応します。
例えば、先ほどプログラムで求めた $\small f(x_1,x_2)=\dfrac{1}{2}\sin x_1-\cos x_2$ の
( 1.57079… , 3.14159… )
という停留点における固有値は
[-0.49960… -0.99920…]
となっており、いずれも負です。このことから、この点は極大点だと判断できます。また、
( 1.57079… , 0.0 )
という停留点における固有値は
[-0.49960… 0.99920…]
となっており、$\omega_{1}$のみが負です。このことから、この点は鞍点だと判断できます。また、固有値$\omega_{1}$に対応する固有ベクトル$$\mathbf{v}_{1}=\left[\begin{array}{l}
1.0 \\
0.0
\end{array}\right]$$は「虚の振動方向」に対応しており、その方向に沿って目的関数が成す曲面が「峠」になっていることを意味しています。
※目的関数が化学的なポテンシャルエネルギー面に対応する場合、この方向に沿って曲面を降下する (質量加重) 最急降下経路は「固有反応座標」(Intrinsic Reaction Coordinate;IRC) と呼ばれるものに相当します。
他の停留点に対しても同様に、固有値から極値判定をすることができます。多変数関数の極値判定については「ヘッセ行列による多変数関数の極値判定」のページで詳しく解説しています。鞍点と「虚の振動数」の関係についても解説しているので参考にして下さい。
※参考文献:
「新しい量子化学―電子構造の理論入門〈上〉」
「Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory」
停留点チャレンジ
“Test functions for optimization” というWikipediaのページに様々な最適化手法のベンチマーク用の関数が掲載されています。
例えば、Himmelblau’s function(ヒンメルブラウの関数)は以下のように定義される2変数関数です。
def f(x, y):
return (x**2 + y -11)**2 + (x + y**2 - 7)**2
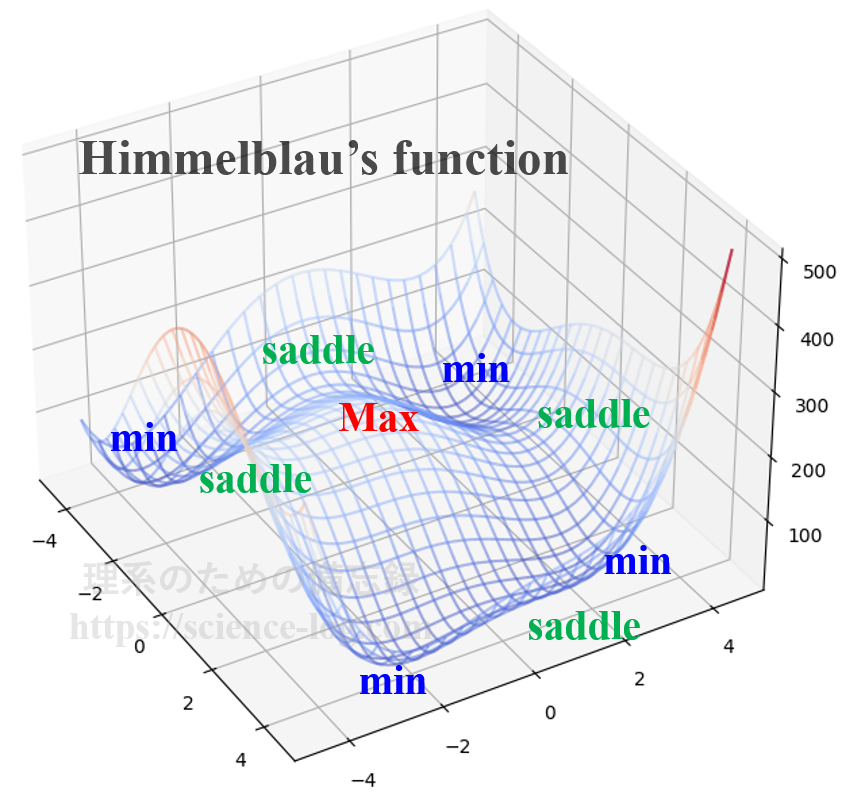
手頃な練習素材にちょうど良いので、9個の停留点をすべて見つけてみましょう! 管理人の手元のプログラムでは、以下のような軌跡で鞍点を見つけることができました。濃い緑色の点が初期位置、赤色の点が到達点です。
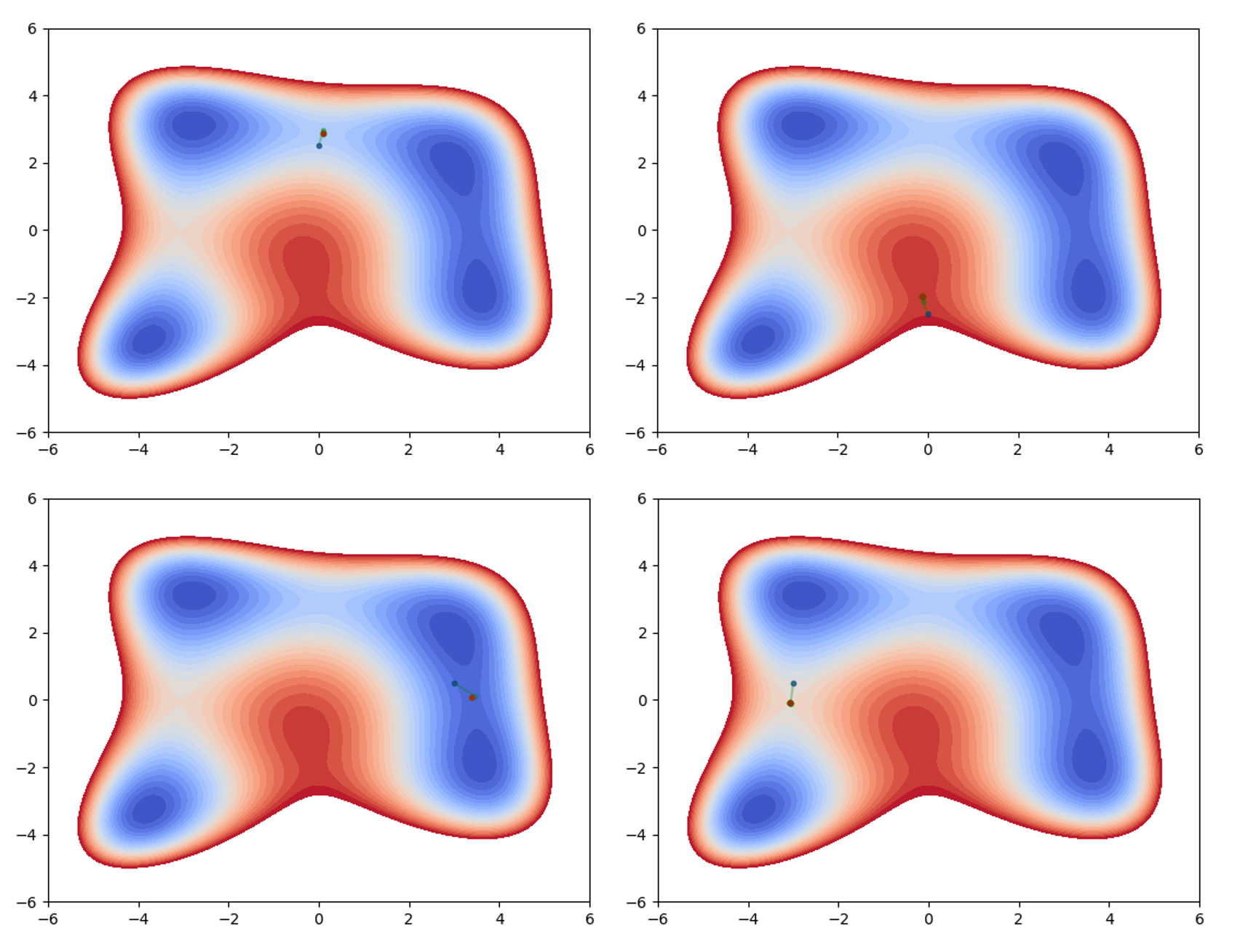 (画像が小さくて見にくい場合は別のタブで開いて見て下さい)
(画像が小さくて見にくい場合は別のタブで開いて見て下さい)
極大点や極小点についてもニュートン法で同様に見つけることができます。ここで便宜上、それぞれの停留点を以下の図のように名前を付けておきます。
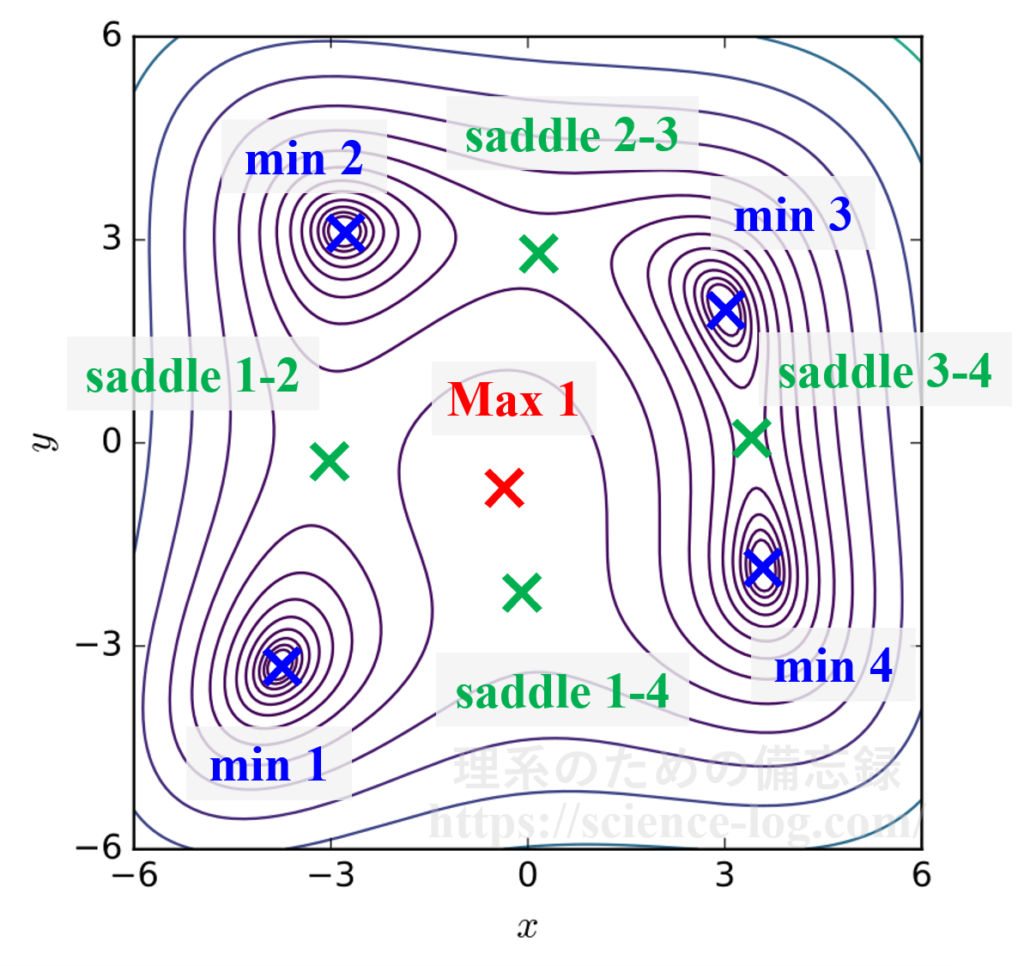
各停留点の座標は以下のようになっており、値の他に固有値と固有ベクトルも載せています(ここで固有ベクトルは単位ベクトルになるように規格化しています)。
saddle 1-2
( -3.073025749300209 , -0.08135304638107348 )
z = 104.01516291755811
[ 72.26089122 -39.93119675]
[[ 0.99301482 0.11798967]
[-0.11798967 0.99301482]]
saddle 2-3
( 0.08667750226556875 , 2.8842546996855103 )
z = 67.71915008752615
[-31.76834648 75.82199609]
[[-0.99433751 -0.10626814]
[ 0.10626814 -0.99433751]]
saddle 3-4
( 3.3851541836492998 , 0.07385187936015292 )
z = 13.31192627040559
[ 97.44009285 -13.99573032]
[[ 0.99216722 -0.12491682]
[ 0.12491682 0.99216722]]
saddle 1-4
( -0.1279613484073797 , -1.9537149746627236 )
z = 178.33723920192745
[-49.20102655 20.77931712]
[[-0.993663 0.11240036]
[-0.11240036 -0.993663 ]]
min 1
( -3.7793102533892027 , -3.2831859912902943 )
z = 7.044847776975894e-21
[133.78561493 70.71435445]
[[ 0.84983348 0.52705128]
[-0.52705128 0.84983348]]
min 2
( -2.8051180869527372 , 3.131312518250689 )
z = 5.435251636972771e-25
[64.84037255 80.55007156]
[[-0.99652071 -0.08334554]
[ 0.08334554 -0.99652071]]
min 3
( 2.999999999999998 , 2.0000000000000036 )
z = 2.335028279454195e-28
[82.28427094 25.71572879]
[[ 0.92387953 -0.38268343]
[ 0.38268343 0.92387953]]
min 4
( 3.5844283403304984 , -1.8481265269644915 )
z = 1.120119376541419e-25
[105.41890798 28.69067719]
[[ 0.99586064 -0.09089321]
[ 0.09089321 0.99586064]]
Max 1
( -0.27084459372962016 , -0.9230385619374777 )
z = 181.61652152258273
[-45.9343729 -18.01447332]
[[-0.99173447 0.12830718]
[-0.12830718 -0.99173447]]
以上が9個の全停留点の情報です。初期値や数値微分の仕様によっては数値が厳密に一致するとは限りませんが、概ね一致していれば正しく見つけられていると言って良いでしょう。
ここでも固有値を確認しておくと、minでは2つの固有値がいずれも正、saddleでは1つのみ負、Maxでは2つの固有値がいずれも負になっています。
また、例えばsaddle 1-2においては固有値$\omega_2$が負なので、峠方向の固有ベクトルが$$\mathbf{v}_2=\left[\begin{array}{c} -0.11798967 \\ 0.99301482 \end{array}\right]$$で、尾根方向(固有値が正の方向)の固有ベクトルが$$\mathbf{v}_1=\left[\begin{array}{c} 0.99301482 \\ 0.11798967 \end{array}\right]$$になっていることも確かめられます。ここで例えば、saddle 1-2の座標を初期値として$\mathbf{v}_2$の前後の方向に最急降下法で下っていくことで得られる経路は、山登りに例えるとmin 1とmin 2を繋ぐ「最も低い標高の道を通って」行き来する経路になります。
まとめ
今回試したのは2変数関数ですが、最適化手法のベンチマーク用の関数には3次以上の関数も用意されています。原理的には多変数関数でも上記と同様の解析が可能です。その場合、図形的な意味付けは難しくなりますが、ニュートン法とヘッセ行列の固有値と固有ベクトルという道具を使って多次元空間内の停留点を探し出して分類することはできます。興味のある方は是非チャレンジしてみて下さい!
このようにニュートン法は停留点を求めることのできるアルゴリズムですが、時に収束がうまくいかないという問題点があります。これはヘッセ行列の(半)正定値性や正則性が常に保証されている訳ではなく、ニュートン法が破綻するケースが存在するためです。次回は、この弱点を克服するアルゴリズムである「準ニュートン法」について紹介します。

“【最適化問題の基礎】ニュートン法で停留点を探す(鞍点と固有値の関係)” への3件の返信