「コッホ雪片」(Koch snowflake) とは、スウェーデンの数学者ヘルゲ・フォン・コッホ (Helge von Koch:1870年~1924年) が考案したフラクタル図形の一種です。
 図.コッホ雪片
図.コッホ雪片
元々は「コッホ曲線」というものがあり、これを三角形の各辺としたものが「コッホ雪片」です。コッホ雪片の周長は無限の長さを持つのに対し、周で囲まれた面積は有限値をとります。今回は北大後期の入試問題から、コッホ雪片に関する問題を取り上げてみます。
《問題》
1辺の長さが$a$の正三角形$D_{0}$から出発して、多角形$D_{1}$、$D_{2}$、$\cdots$、$ D_{n}$、$\cdots$ を次のように定める。
(ⅰ) $\mathrm{AB}$を$D_{1}$の1辺とする。辺$\mathrm{AB}$を$3$等分し、その分点を$\mathrm{A}$に近い方から$\mathrm{P}$、$\mathrm{Q}$とする。
(ⅱ) $\mathrm{PQ}$を1辺とする正三角形$\mathrm{PQR}$を$D_{n-1}$の外側に作る。
(ⅲ) 辺$\mathrm{AB}$を折線$\mathrm{APRQB}$で置き換える。
$D_{1}$のすべての辺に対して(ⅰ)~(ⅲ)の操作を行って得られる多角形を$D_{n}$とする。
以下の問いに答えよ。
(1)$D_{n}$の周の長さ$L_n$を$a$と$n$で表せ。
(2)$D_{n}$の面積$S_n$を$a$と$n$で表せ。
(3)$\displaystyle \lim_{n \to \infty} S_n$を求めよ。
(2010年北海道大学 後期第3問)
《考え方》
図を使って考えると分かりやすいでしょう。正三角形と書いてありますが、まずは1辺に注目して周の長さや面積の増分を調べます。図形絡みの無限等比級数の典型題なので規則性(数列)さえ見つけられれば(3)はサービス問題です。
以下では多角形 $D_{n}$ の一辺の長さと辺の本数を数列にして考えることにします。
解答例
(1)
多角形 $D_{n}(n=0,1,2, \cdots)$ の一辺の長さを$a_{n}$とし、辺の本数を$x_{n}$とする。
$D_0$は一辺の長さが$a$の正三角形であるから、$$a_0=a,\, x_0=3 \quad \cdots ①$$となる。
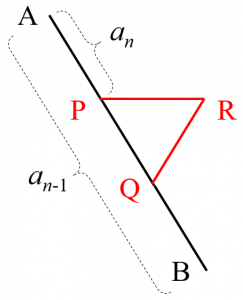
$D_{n-1}$の各辺に対して(ⅰ)~(ⅲ)の操作を1回ずつ行うと辺の長さは$\dfrac{1}{3}$倍され、辺の本数は$4$倍になる。
故に$$\left\{\begin{array}{ll}
a_{n}=\dfrac{1}{3} a_{n-1}, & \cdots ② \\
x_{n}=4 x_{n-1} & \cdots ③
\end{array}\right.$$が成り立つ。①と②より、$$a_{n}=a\left(\dfrac{1}{3}\right)^{n} \quad(n=0,1,2, \cdots)$$を得る。また、①と③より、$$x_{n}=3 \cdot 4^{n} \quad(n=0,1,2, \cdots)$$を得る。よって多角形 $D_{n}(n=0,1,2, \cdots)$ の周の長さ$L_n$は$$\begin{align}
L_{n} &= a_{n} x_{n} \\
&= a\left(\frac{1}{3}\right)^{n} \cdot 3 \cdot 4^{n} \\
&= \color{red}{3 a\left(\frac{4}{3}\right)^{n}}
\end{align}$$と求められる。
(2)
$D_{n-1}$の各辺に対して(ⅰ)~(ⅲ)の操作を1回ずつ行うと以下のように$D_n$が生成する。
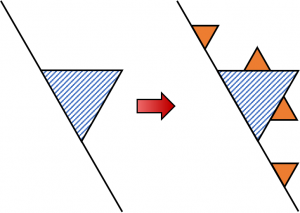
$D_{n-1}$の$x_{n-1}$本の各辺には新たに一辺の長さが$a_n$の正三角形が付け加えられるから、面積の増分は$$S_{n}-S_{n-1}=\dfrac{\sqrt{3}}{4}\left(a_{n}\right)^{2} \cdot x_{n-1}$$で与えられる。これと(1)の結果より、$$\begin{align}
S_{n}-S_{n-1} &=\dfrac{\sqrt{3}}{4}\left\{a\left(\dfrac{1}{3}\right)^{n}\right\}^{2} \cdot 3 \cdot 4^{n-1} \\
&=\dfrac{\sqrt{3}}{12} a^{2}\left(\dfrac{4}{9}\right)^{n-1} \quad(n \geqq 1)
\end{align}$$となる。これは階差数列になっているので、$$\begin{align}
S_{1}-S_{0}&=\dfrac{\sqrt{3}}{12} a^{2} \\
S_{2}-S_{1}&=\dfrac{\sqrt{3}}{12} a^{2}\left(\dfrac{4}{9}\right) \\
S_{3}-S_{2}&=\dfrac{\sqrt{3}}{12} a^{2}\left(\dfrac{4}{9}\right)^{2} \\
& \vdots \\
S_{n}-S_{n-1}&=\dfrac{\sqrt{3}}{12} a^{2}\left(\dfrac{4}{9}\right)^{n-1}
\end{align}$$の辺々を加えて$$\small \begin{align}
S_{n}-S_{0} &=\dfrac{\sqrt{3}}{12} a^{2}\left\{1+\dfrac{4}{9}+\left(\dfrac{4}{9}\right)^{2}+\cdots+\left(\dfrac{4}{9}\right)^{n-1}\right\} \\
&=\dfrac{\sqrt{3}}{12} a^{2} \cdot \dfrac{1-\left(\dfrac{4}{9}\right)^{n}}{1-\dfrac{4}{9}} \\
&=\dfrac{3 \sqrt{3}}{20} a^{2}\left\{1-\left(\dfrac{4}{9}\right)^{n}\right\}
\end{align}$$と整理できる。ここで、$S_{0}=\dfrac{\sqrt{3}}{4} a^{2}$ より、$$\begin{align}
S_{n} &=\dfrac{\sqrt{3}}{4} a^{2}+\dfrac{3 \sqrt{3}}{20} a^{2}\left\{1-\left(\dfrac{4}{9}\right)^{n}\right\} \\
&=\sqrt{3} a^{2}\left\{\dfrac{2}{5}-\dfrac{3}{20}\left(\dfrac{4}{9}\right)^{n}\right\}
\end{align}$$を得る。これは $n=0$ のときも成立するから、$$S_n=\color{red}{\sqrt{3} a^{2}\left\{\dfrac{2}{5}-\dfrac{3}{20}\left(\dfrac{4}{9}\right)^{n}\right\}}$$となる。
(3)
(2)の結果より、$$\lim _{n \to \infty} S_{n}=\color{red}{\dfrac{2 \sqrt{3}}{5} a^{2}}$$である。
(コメント)
問題文からは何となく難しそうな雰囲気がしますが、パターンさえ掴んでしまえば実は単純な問題であると分かります。
上で見たように、コッホ雪片の面積はもとの正三角形の面積の$\dfrac{8}{5}$倍に限りなく近づきます。因みに、フラクタル幾何学において「$1/k$ 倍に縮めると、もとの図形を作るには $N = k^D$ 個の図形が必要となる」という意味で「フラクタル次元$D$」というものが定義されています。この定義に照らせば、コッホ雪片のフラクタル次元は$$\dfrac{\log 4}{\log 3} \approx 1.262$$となります。これは$1$次元より大きく$2$次元より小さいので、周長は無限大に発散し、面積は有限値に収束することに対応しています。フラクタル図形について興味のある方は「ちょっと面白い「無限」の話」の記事も是非ご覧下さい!
