今回は今年の阪大理系数学で出題された求積問題を取り上げます。
3辺の長さの和が$2$である三角形$\mathrm{ABC}$において、辺$\mathrm{BC}$の長さを$a$、辺$\mathrm{CA}$の長さを$b$で表す。三角形$\mathrm{ABC}$を辺$\mathrm{BC}$を軸として1回転させてできる回転体の体積を$V$とする。以下の問いに答えよ。
(1)$a$の値を固定して$b$の値を変化させるとき、$V$が最大になるのは、三角形$\mathrm{ABC}$が辺$\mathrm{BC}$を底辺とする二等辺三角形となるときである。これを示せ。
(2)$a$、$b$の値をともに変化させるとき、$V$の最大値と、最大値を与える$a$、$b$の値をそれぞれ求めよ。
(2020年大阪大学 前期理系第5問)
考え方
三角形$\mathrm{ABC}$の3辺の長さの和が一定という拘束条件が課された、よくあるタイプの最小・最大値の問題です。(1)は座標に置いて機械的に証明するとラクです。(2)は(1)の結論を利用するだけで複雑な計算は全く不要です。
解答例
(1)
$\mathrm{B}\left(-\dfrac{a}{2}, 0\right)$、$\mathrm{C}\left(\dfrac{a}{2}, 0\right)$ となるように座標軸をとる。$b$の値を変化させると頂点$\mathrm{A}$は$$\mathrm{AB}+\mathrm{AC}=2-a$$を満たしながら動くから、点$\mathrm{A}$の描く軌跡は$\mathrm{B}$、$\mathrm{C}$を焦点とする長軸の長さが $2-a$ であるような楕円(軸上の2点を除く)である。
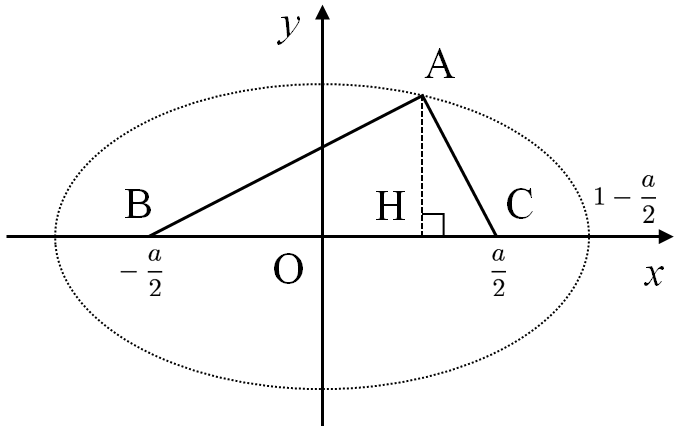
点$\mathrm{A}$から辺$\mathrm{BC}$に垂線$\mathrm{AH}$を下ろし、$\mathrm{H}(x, 0)$とする。このとき $-1+\dfrac{a}{2}<x<1-\dfrac{a}{2}$ が成り立つ。
(ⅰ)$-1+\dfrac{a}{2} <x \leqq -\dfrac{a}{2}$のとき、
$$\small \begin{aligned} V &=\dfrac{1}{3} \pi \mathrm{AH}^{2} \left(\dfrac{a}{2}-x\right)-\dfrac{1}{3} \pi \mathrm{AH}^{2} \left(-\dfrac{a}{2}-x\right) \\ &=\dfrac{\pi a}{3} \mathrm{AH}^{2} \end{aligned}$$となる。
(ⅱ)$-\dfrac{a}{2} <x < \dfrac{a}{2}$のとき、
$$\small \begin{aligned} V &=\dfrac{1}{3} \pi \mathrm{AH}^{2} \left(\dfrac{a}{2}-x\right)+\dfrac{1}{3} \pi \mathrm{AH}^{2} \left(x+\dfrac{a}{2}\right) \\ &=\dfrac{\pi a}{3} \mathrm{AH}^{2} \end{aligned}$$となる。
(ⅲ)$\dfrac{a}{2} \leqq x < 1-\dfrac{a}{2}$のとき、
$$\small \begin{aligned} V &=-\dfrac{1}{3} \pi \mathrm{AH}^{2} \left(x-\dfrac{a}{2}\right)+\dfrac{1}{3} \pi \mathrm{AH}^{2} \left(x+\dfrac{a}{2}\right) \\ &=\dfrac{\pi a}{3} \mathrm{AH}^{2} \end{aligned}$$となる。
(ⅰ)~(ⅲ)より、いずれの場合でも$$V=\dfrac{\pi a}{3} \mathrm{AH}^{2}$$と表せることが分かる。
したがって$V$が最大となるのは垂線$\mathrm{AH}$が最大となるときであるから、これは点$\mathrm{A}$が$\mathrm{BC}$の垂直二等分線上にくるとき、つまり三角形$\mathrm{ABC}$が辺$\mathrm{BC}$を底辺とする二等辺三角形となるときである。
□
(2)
(1)より、$V$が最大となるのは三角形$\mathrm{ABC}$が辺$\mathrm{BC}$を底辺とする二等辺三角形となるときである。このとき$$a+2b=2$$となり、三平方の定理より$$\small \mathrm{AH}^2=\left(1-\dfrac{a}{2}\right)^{2}-\left(\dfrac{a}{2}\right)^{2}=1-a$$となるから、$$\small \begin{aligned}
V & \leqq \dfrac{\pi a}{3}(1-a) \\
&=-\dfrac{\pi}{3}\left(a-\dfrac{1}{2}\right)^{2}+\dfrac{\pi}{12} \\
& \leqq \dfrac{\pi}{12} \ \ \left(\text{等号成立は } a=\dfrac{1}{2} \text{ のとき}\right)
\end{aligned}$$となる。
以上より、$\color{red}{a=\dfrac{1}{2}}$、$\color{red}{b=\dfrac{3}{4}}$ のとき、$V$は最大値 $\color{red}{\dfrac{\pi}{12}}$ をとる。

本問は2変数関数の問題ですが、丁寧な誘導が付いているので落とせません。三角形$\mathrm{ABC}$は対称な図形なので(1)が無くても体積$V$が最大になる状況(三角形$\mathrm{ABC}$が二等辺三角形になること)の見当が付けられることが望ましいです。
今年の阪大数学は全体的にかなり易化しました。本問は数Ⅲ範囲の求積問題ということで出題されたようですが、積分不要の問題でありほとんど差が付かなかったのではないでしょうか。来年は確実に難化すると思われますので、やや複雑な定積分計算や空間図形の求積はしっかり対策しておきましょう。