曲面上の停留点間の最急降下経路に関する話題です。計算化学分野の内容を多分に含みます。
化学反応経路の分岐
量子化学の世界では、分子の座標(原子核の位置)に対応するシュレーディンガー方程式をコンピューターによって解き、その構造におけるエネルギーを計算します。普通、量子化学計算による反応経路探索においては静的な化学ポテンシャルを考えます。つまり、分子の構造に「揺らぎ」が無い絶対零度の状態のエネルギー面上で化学反応経路の性質を議論しています。
※振動数解析などにより自由エネルギーが得られる場合は、自由エネルギーに基づいて議論されます。
しかしこれでは温度に依存する熱力学的な効果を記述することができないため、現実の系に存在する分子の動力学的な性質(ダイナミクス)を反映させることは困難です。この点において、ポテンシャルエネルギー面上における反応経路の取り扱いが不正確になってしまう場合があります。
反応経路は動力学的に分岐することがあります。物質Aが化学的に変化して物質Bと別の物質Cのいずれかが生じる、といったシチュエーションは理論的に考えられるだけでなく、実際の有機化学反応などでも見られる現象です。
もっと具体的に説明すると、例えば、共役ジエンにアルケンが付加して6員環構造を生じる「ディールス・アルダー反応」などのペリ環状反応には、1種類の反応物が複数の生成物を一定の割合で生じる反応が数多く知られています。ブタジエンとアレンのペリ環状反応では4員環化合物と6員環化合物の2種類の生成物を与えることが知られています。
このような生成物の夾雑現象は、ポテンシャルエネルギー面上において「経路分岐」(bifurcation) が発生していることに由来する場合があります。以下の図はポテンシャルエネルギー面上で起きている経路分岐の模式図です。左側の極小点(reactant)から出発して1つ目の遷移状態(transition state;TS)を超えると2つ目の遷移状態に衝突します。その過程でポテンシャル面の曲率が正から負に変わるような領域に差し掛かり、ここでエネルギーが最小になるような経路(「最小エネルギー経路」=minimum energy path;MEP と呼ばれる)を選んで手前側の極小点(product 1)へと下っていきます。一方で、分子には運動エネルギーが存在するので、2つ目の遷移状態を超えられるだけの余分なエネルギーがあれば、一部の分子は奥側の極小点(product 2)にも下っていきます。これが経路分岐の概略です。
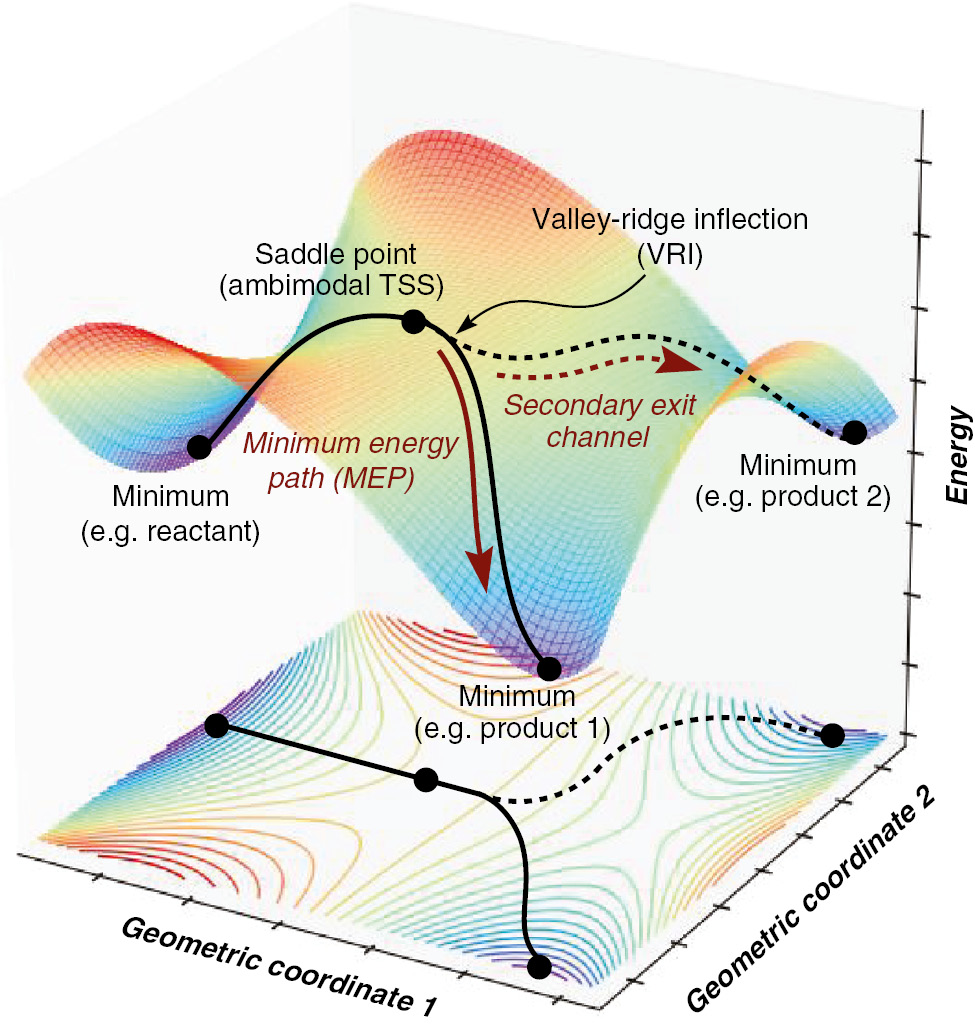
図.$z=2x^5-7x^2-5xy+y^2+2$ を元に作成されたbifurcationの概念図
(Pure Appl. Chem. 2017; 89(6): 679–698 より引用)
このような経路分岐は最急降下経路が “valley-ridge inflection point” (VRI)「谷尾根変曲点」と呼ばれる点に差し掛かったときに発生すると考えられています。VRIは「ヘッセ行列の固有値がゼロであり、勾配ベクトルが対応する固有ベクトルに垂直であるような点」として数学的に定義されます。例えばメタクロレインの二量化では全く同じ生成物を与えるものの、同位体効果を調べた研究グループにより2通りの生成経路が存在することが報告されています。これは経路分岐がポテンシャル面の対称性が高いほど生じやすいことを裏付けています。
化学反応の理論解析で頻繫に用いられている遷移状態理論(Transition state theory;TST)では、遷移状態とポテンシャルの極小点は1対1に対応しているものと考えるため、複数の生成物を与える経路分岐のような現象を正しく考慮できないという問題があります。静的なポテンシャル面の最小エネルギー経路を追跡する他に、分子動力学(molecular dynamics;MD)シミュレーションなどを使えば動的な化学反応経路の追跡が可能です。MDシミュレーションは反応の分岐比を予測して実験的な生成物の生成比と比較するためによく使用されており、経路分岐を検出することができます。
※模式図では単なる2変数関数で経路分岐が説明されていますが、実際の化学的ポテンシャルエネルギー面は分子の原子数を$N$とすると $3N-6$ 次元の超曲面になっています。
※参考文献:
“Post-transition state bifurcations gain momentum – current state of the field” by Stephanie R. Hare, Dean J. Tantillo(2017年)
“Diels–Alder Reactions of Allene with Benzene and Butadiene: Concerted, Stepwise, and Ambimodal Transition States” by Hung V. Pham, K. N. Houk(2014年)
“Racing Carbon Atoms. Atomic Motion Reaction Coordinates and Structural Effects on Newtonian Kinetic Isotope Effects” by Ivonne L. Andujar-De Sanctis, Daniel A. Singleton(2012年)
経路分岐を体感してみる
2変数関数$f(x, y)$について $z=f(x, y)$ のグラフは3次元の曲面を描きます。たった2変数の関数でも上図のような経路分岐が観察できるので、ちょっとした考察くらいはできます。
適当にアレンジした多峰性の2変数関数$$\begin{align} f(x, y)=& \dfrac{1}{2} e^{\sin (x-2)+\cos y}+e^{\sin (x-y)-\cos y} \\ &+\dfrac{1}{14} e^{\sin y+3 \cos (x-y)}+\dfrac{2}{e^{x+y-3}+1}+\dfrac{e^{\frac{x^{2}}{3}+\frac{y^{2}}{5}}}{1000} \end{align}$$について考えます。曲面の等高線図(青色が濃いほど関数値が小さい)は以下のようになり、各停留点に適当な名前を付けています。小文字のmは極小点、大文字のMは極大点、sは鞍点に対応しています。極値の点の番号は適当に付けており、鞍点は隣接する極小点の番号を取っています。
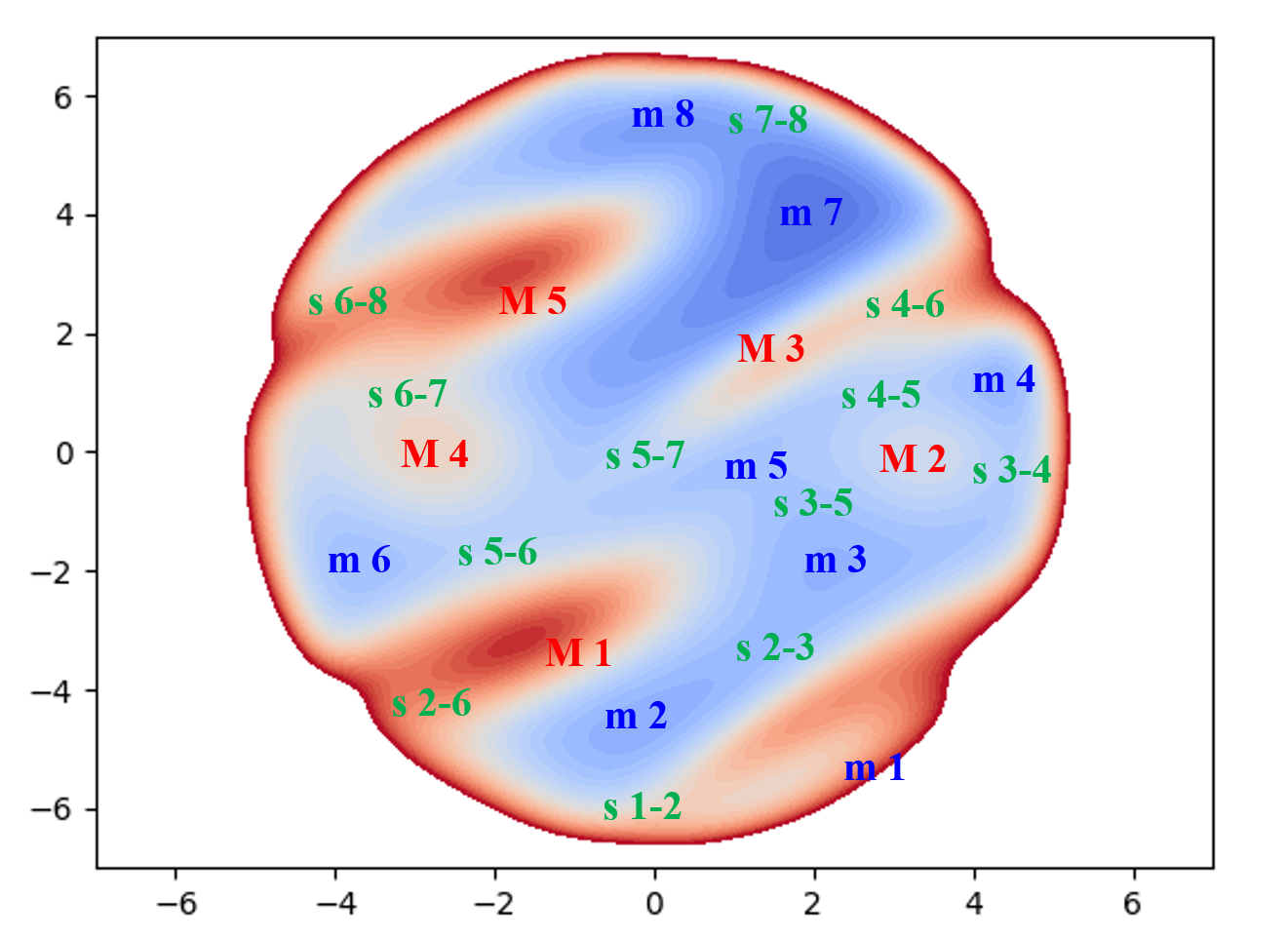
以下に、ニュートン法によって求めた停留点の座標の情報をまとめておきます。ニュートン法の初期値、停留点の座標、関数の値、固有値、固有ベクトルの順で出力しています。
m 1
初期値( 0.0 , -6.0 )
( 1.4086361787327064 , -5.658809316260772 )
z = 5.786351992929754
[ 1.14442798 16.37489135]
[[-0.86604243 0.49997051]
[-0.49997051 -0.86604243]]
m 2
初期値( -0.2 , -5.7 )
( -0.1534676564241066 , -4.57828215659672 )
z = 2.7759045767270636
[0.54849511 3.18185425]
[[-0.80732635 0.59010521]
[-0.59010521 -0.80732635]]
m 3
初期値( 2.0 , -2.2 )
( 2.1997561975738664 , -1.9584626867041848 )
z = 2.9388130001023183
[1.18091723 0.78417752]
[[ 0.80864711 0.58829402]
[-0.58829402 0.80864711]]
m 4
初期値( 5.0 , 1.2 )
( 4.313644005998416 , 1.1593143232803698 )
z = 3.0305769127824016
[6.31913802 3.75058481]
[[ 0.96440424 -0.26443234]
[ 0.26443234 0.96440424]]
m 5
初期値( 1.5 , -0.0 )
( 0.9491645285652016 , -0.2535674327975252 )
z = 3.5017193990520292
[0.27883967 2.48561566]
[[-0.87126064 0.49082063]
[-0.49082063 -0.87126064]]
m 6
初期値( -5.0 , -1.2 )
( -3.677845437568093 , -1.9163715276002327 )
z = 3.3598513299661534
[2.15189449 1.64506825]
[[ 0.86078997 -0.50896034]
[ 0.50896034 0.86078997]]
m 7
初期値( 1.7 , 4.2 )
( 2.006200846410346 , 4.038093623114429 )
z = 1.2312275482293922
[1.54831406 1.06626116]
[[ 0.9533115 0.30198871]
[-0.30198871 0.9533115 ]]
m 8
初期値( 0.0 , 5.2 )
( 0.13360502819497327 , 5.441000744912198 )
z = 2.2486368497581024
[0.80261158 5.6144775 ]
[[-0.98171251 0.19036952]
[-0.19036952 -0.98171251]]
s 1-2
初期値( 0.2 , -5.9 )
( 0.5911185541395549 , -5.840355227348794 )
z = 6.091100380299775
[-5.95858232 4.55970131]
[[-0.91356389 -0.40669524]
[ 0.40669524 -0.91356389]]
s 2-3
初期値( 1.5 , -3.0 )
( 1.3830211871216698 , -3.1351298654416966 )
z = 3.158261239473254
[ 2.78256234 -0.46219622]
[[ 0.78615827 0.61802523]
[-0.61802523 0.78615827]]
s 2-6
初期値( -2.9 , -3.3 )
( -3.079694456117682 , -3.8169362267214875 )
z = 8.522333100905895
[ 4.54758333 -6.94566506]
[[ 0.94965627 -0.31329374]
[ 0.31329374 0.94965627]]
s 3-4
初期値( 4.5 , -0.0 )
( 4.442366502655995 , -0.21089842113555415 )
z = 3.894918124802819
[ 7.50516247 -1.48775368]
[[ 0.99566663 0.09299444]
[-0.09299444 0.99566663]]
s 3-5
初期値( 1.5 , -1.0 )
( 1.379372606862197 , -0.4786865554475489 )
z = 3.5559714727292393
[ 0.76555478 -1.20964399]
[[ 0.75701428 -0.65339833]
[ 0.65339833 0.75701428]]
s 4-5
初期値( 3.5 , 1.0 )
( 2.9886304968351096 , 1.0272104461681844 )
z = 4.046069332449557
[-1.45233016 3.02884685]
[[-0.9915228 0.12993279]
[-0.12993279 -0.9915228 ]]
s 4-6
初期値( 3.5 , 2.2 )
( 2.5808737214289073 , 2.241725635116187 )
z = 6.012002997696764
[ 0.92723124 -14.71620121]
[[ 0.86468909 -0.50230745]
[ 0.50230745 0.86468909]]
s 5-6
初期値( -2.0 , -1.7 )
( -1.9600748749620056 , -1.3395152803097021 )
z = 4.060821934369255
[-0.57428115 3.9715636 ]
[[-0.88642364 0.46287485]
[-0.46287485 -0.88642364]]
s 5-7
初期値( -1.0 , -0.7 )
( -0.8901369277657292 , -0.6493631310387875 )
z = 3.918861049829654
[ 0.4481126 -1.54723339]
[[ 0.79069046 -0.61221613]
[ 0.61221613 0.79069046]]
s 6-7
初期値( -3.0 , 1.0 )
( -3.1159520248822377 , 0.945523410719906 )
z = 5.531203504201209
[-2.18926598 2.8553998 ]
[[-0.97414597 0.22591954]
[-0.22591954 -0.97414597]]
s 6-8
初期値( -4.0 , 2.0 )
( -3.5658006421874 , 2.358148230699719 )
z = 7.942261760676404
[ 1.25342776 -12.88856506]
[[ 0.9031012 -0.42942779]
[ 0.42942779 0.9031012 ]]
s 7-8
初期値( 1.0 , 5.0 )
( 0.7213665810278206 , 5.354689366964271 )
z = 2.31941895434561
[-1.36725747 3.32124999]
[[-0.90274005 -0.43018648]
[ 0.43018648 -0.90274005]]
M 1
初期値( -1.5 , -3.0 )
( -1.7079408169126866 , -3.200249957507587 )
z = 9.784379583152711
[ -2.28072237 -17.92533667]
[[ 0.86180099 -0.50724654]
[ 0.50724654 0.86180099]]
M 2
初期値( 3.7 , 0.0 )
( 3.3958809693167877 , -0.06959462086785176 )
z = 4.786960187630291
[-2.61664903 -3.04548839]
[[ 0.82536242 0.56460328]
[-0.56460328 0.82536242]]
M 3
初期値( 1.7 , 1.6 )
( 1.6925276303396097 , 1.6076395635220364 )
z = 6.196133687522351
[ -0.80039139 -23.75774191]
[[ 0.78181107 -0.62351539]
[ 0.62351539 0.78181107]]
M 4
初期値( -2.7 , 0.0 )
( -2.794616613610473 , 0.07916833974018259 )
z = 5.965024848304088
[-3.55809756 -2.63694692]
[[-0.79534787 0.60615325]
[-0.60615325 -0.79534787]]
M 5
初期値( -2.0 , 3.0 )
( -1.8186002491037492 , 3.0154282020752246 )
z = 9.475693316932386
[ -2.57704317 -17.45138019]
[[ 0.86906236 -0.49470256]
[ 0.49470256 0.86906236]]
極値判定の方法は「ヘッセ行列による多変数関数の極値判定」のページ、停留点をプログラムによって求める方法については「【最適化問題の基礎】ニュートン法で停留点を探す(鞍点と固有値の関係)」のページを参考にして下さい。
この2変数関数$f(x, y)$には3つの「経路分岐」が存在します。列挙すると以下の通りです。
s 4-6 → s 4-5 → m 4 / m 5
s 5-6 → s 5-7 → m 5 / m 7
s 6-8 → s 6-7 → m 6 / m 7
対応する鞍点から「峠方向」の前後に下った経路を図示すると以下のようになります。経路の出発点である鞍点は緑色の丸、経路の到達点である極小点は赤色の丸で表示しています。赤色の曲線が経路分岐している降下経路であり、青色の曲線はその途中で衝突する鞍点からの降下経路を描画したものです。
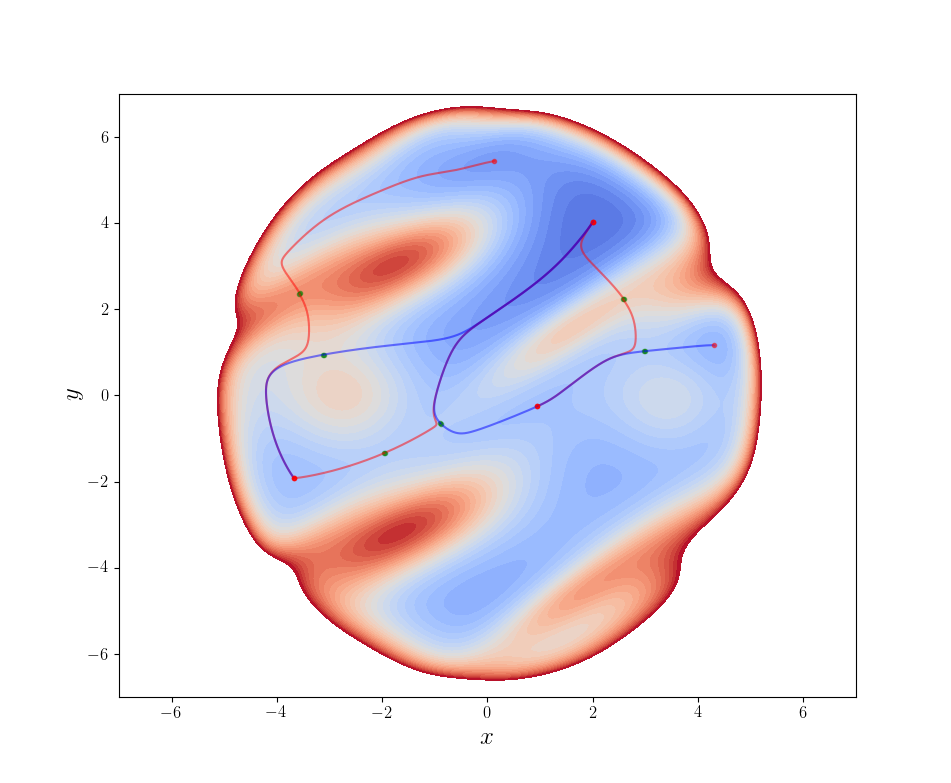
※これらの経路は、鞍点の近くに「限りなくゆっくりと流れる水」を流したときにその水流が辿る軌跡になっています。実際の水流には「勢い」があるため、山にぶつかっても勢いよく乗り越えてしまうことがありますが、そういった場合は考えないという意味の比喩表現です。数学的には単なる「最急降下経路」として定義されます。
赤色の曲線は青色の曲線と途中で合流しています。赤色の曲線が衝突する鞍点を「低い方の鞍点」と呼ぶことにすると、赤色の曲線は低い方の鞍点が繋ぐ2つの極小点のうちの一方に到達しています。このことは、ある鞍点(遷移状態)を通過した分子は両側のエネルギー極小点に降下していくはずなのに、最急降下経路を辿っているだけではそのうちの一方しか見つけられない(最小エネルギー経路(MEP)のみが得られている)ことを意味しています。
すべての鞍点からの降下経路を描画すると以下のようになります。経路分岐に関係しない鞍点からの降下経路は緑色の曲線で表示しています。
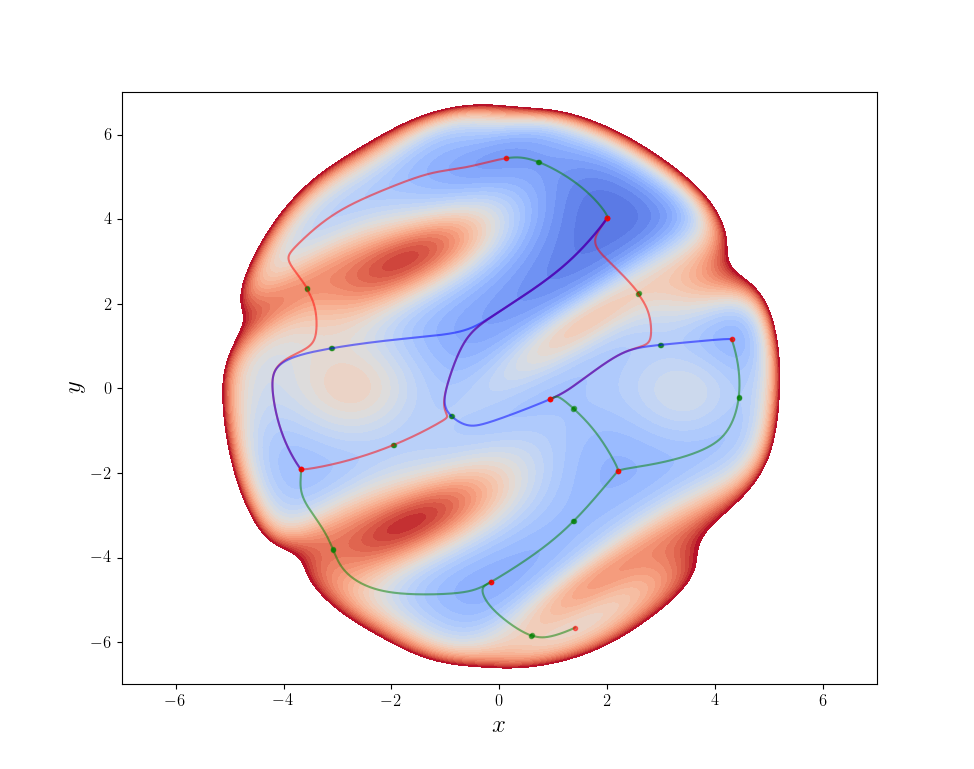
MEPの追跡にはもう一つの問題点があります。最急降下法ではどんなに「曲がった」経路でも得られてしまうため、例えば分子が熱的に分解して一部分が解離する経路などが正しく求められないことがあります。このような反応経路は通常、MEPから大きく逸れた軌跡を描くため、静的なポテンシャル面を調べているだけでは見つけることができません。このような固有反応座標(Intrinsic Reaction Coordinate;IRC)に基づく描像からの逸脱は、経路分岐とはまた異なる計算化学の研究課題です。
今は2変数関数を考えているので、横に別の極小点が存在することは見れば直ぐに分かりますが、化合物のポテンシャルエネルギーという多次元関数上では極小点の見落としに繋がりかねません。化学反応を正確に捉えるという観点から、ポテンシャル面上の経路分岐を検出する研究が現在盛んに行われています。
