本稿では正七角形の対角線と「高さ」について成り立つ関係式を紹介します。
正七角形の性質と対角線の関係式
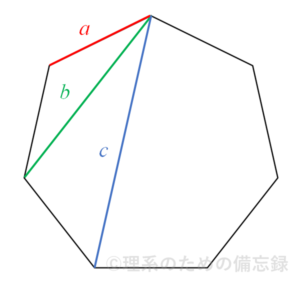
正七角形には2種類の対角線があります。下図のように、1辺の長さを$a$、短い方の対角線の長さを$b$、長い方の対角線の長さを$c$と置きます。
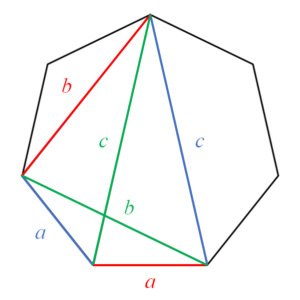
このときトレミーの定理より、配色した四角形の各辺と対角線の長さについて$$\color{green}{bc}\color{black}{}=\color{red}{ab}\color{black}{}+\color{blue}{ca}$$が成り立つので、両辺を$abc$で割って関係式$$\dfrac{1}{a}=\dfrac{1}{b}+\dfrac{1}{c}$$を得ます。これは正七角形について成り立つ最も有名な等式の一つです。この他にも様々な証明法が知られています。
※「トレミーの定理」とは、円に内接する四角形$\mathrm{ABCD}$において、辺の長さに関する等式:$$\mathrm{AC\cdot BD=AD\cdot BC+AB\cdot DC}$$が成り立つという幾何学の定理のこと。高校数学A「平面図形」の範囲で学習する定理です。
※ この等式はレンズの公式(ガウスの結像公式とも呼ばれる)と同じ構造をしていることから、”Optic equation” と名前が付いています。”Optic” とは英語で「光学の」という意味の形容詞です。
また同様に、正七角形から下図の四角形を切り出してトレミーの定理を適用することにより、以下の3つの関係式が得られます。
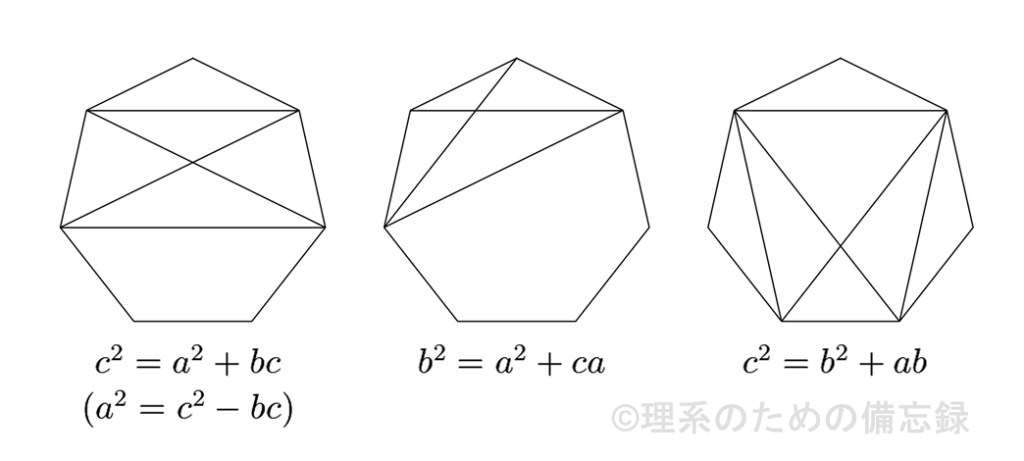
これらを組み合わせることで$$\begin{cases} b^{3}+2b^{2}c-bc^{2}-c^{3}=0 \\ c^{3}-2c^{2}a-ca^{2}+a^{3}=0 \\ a^{3}-2a^{2}b-ab^{2}+b^{3}=0 \end{cases}$$という方程式が得られるので、これらの対角線の長さと辺の長さの比($-b/c$、$c/a$、$a/b$)は3次方程式$$t^{3}-2t^{2}-t+1=0$$の解として与えられます。ただし三角関数を使わずにこの厳密解を表すことは困難です。
※ 近似値を用いると$$b=1.8019377358… \times a$$ $$c=2.2469796037… \times a$$となります。
また、外接円の半径を$R$とするとき、$$a^{2}+b^{2}+c^{2}=7 R^{2}$$という関係式が成り立ちます。これは正弦定理から示すことができるので、後で証明してみましょう。
正七角形の「高さ」と対角線
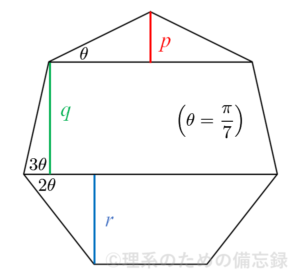
続いて、正七角形の「高さ」というものを考えます。これは正七角形のある頂点から対辺に下ろした垂線として定義される線分の長さを指します。下図は正七角形の高さを2本の対角線で分割した様子を表しています(「高さ」そのものは $p+q+r$ です)。
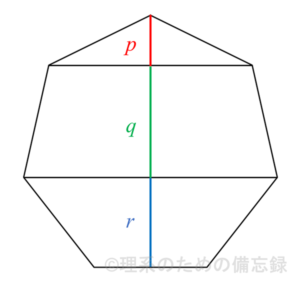
正七角形の1辺の長さが$2$のとき、配色した3本の線分について関係式$$p^2+q^2+r^2=7$$が成り立つことが知られています。美しいですね。
この証明は意外とシンプルです。下図のように $\theta=\dfrac{\pi}{7}$ と置くと、$$\begin{cases} p=2 \sin \theta \\ q=2 \sin 3\theta \\ r=2 \sin 2\theta \end{cases}$$と表せるので、示すべき関係式は$$\sin^2 \theta+\sin^2 2\theta+\sin^2 3\theta=\dfrac{7}{4} \quad \cdots (*)$$となります。
ここで半角公式を用いると$$\begin{aligned} \sin^2 \theta &=\dfrac{1-\cos 2\theta}{2} \\ \sin^2 2\theta &=\dfrac{1-\cos 4\theta}{2} \\ \sin^2 3\theta &=\dfrac{1-\cos 6\theta}{2} \end{aligned}$$となるので、$(*)$式に代入して整理すると$$\cos 2\theta + \cos 4\theta + \cos 6\theta=-\dfrac{1}{2} \quad \cdots (**)$$となります。そこで $\theta=\dfrac{\pi}{7}$ のときに$(**)$が成り立つことを示しましょう。
$\require{cancel}$色々な証明が考えられますが、ここでは少し技巧的な式変形を使って示してみます。まず$(**)$式の両辺に$\sin \theta \ (\ne 0)$を掛けて$$\cos 2\theta \sin \theta+ \cos 4\theta \sin \theta+ \cos 6\theta \sin \theta=-\dfrac{1}{2}\sin \theta$$とします。ここで左辺に積和公式$$\cos \alpha \sin \beta=\dfrac{1}{2}\{\sin (\alpha+\beta)-\sin (\alpha-\beta)\}$$を使うと、$$\small \begin{aligned} (\text{左辺}) &=\dfrac{1}{2}(\cancel{\sin 3\theta}-\sin \theta)+\dfrac{1}{2}(\cancel{\sin 5\theta}-\cancel{\sin 3\theta})+\dfrac{1}{2}(\sin 7\theta-\cancel{\sin 5\theta}) \\ &=-\dfrac{1}{2}\sin \theta +\dfrac{1}{2}\sin 7\theta \\ &=-\dfrac{1}{2}\sin \theta \quad (\because \sin 7\theta=\sin \pi=0) \\ &=(\text{右辺}) \end{aligned}$$となります。よって$(**)$式が成り立つので$(*)$式が成り立ち、関係式$$p^2+q^2+r^2=7$$の成立が示されます。
※ 正七角形の1辺の長さが$a$のときは$$p^2+q^2+r^2=\dfrac{7}{4}a^2$$が成り立ちます。
※ いまは正七角形の場合を考えていますが、正多角形の「高さ」を対角線で内分した線分について類似した等式が成り立ちます。(参考:正多角形の高さ(その2);外部リンク)
先ほど、外接円の半径を$R$とすると関係式$$a^{2}+b^{2}+c^{2}=7 R^{2}$$が成り立つことを紹介しました。

$\theta=\dfrac{\pi}{7}$ と置くと、正弦定理より $\dfrac{a}{2 R}=\sin \theta$、$\dfrac{b}{2 R}=\sin 2 \theta$、$\dfrac{c}{2 R}=\sin 3 \theta$ と表されるので、これらを$(*)$式に代入すると$$\left(\dfrac{a}{2 R}\right)^{2}+\left(\dfrac{b}{2 R}\right)^{2}+\left(\dfrac{c}{2 R}\right)^{2}=\dfrac{7}{4}$$ $$\therefore a^{2}+b^{2}+c^{2}=7 R^{2}$$となり確かに成り立っています。
※ 因みに、これは正$(2n+1)$角形について一般に成り立つ関係式の特殊な場合になっています。正$(2n+1)$角形$\mathrm{A}_{1}\mathrm{A}_{2}\mathrm{A}_{3} \ldots \mathrm{A}_{2n+1}$において対角線の長さをそれぞれ$$\overline{\mathrm{A}_{2 n+1}\mathrm{A}_{k}}=a_{k} \quad (k=1,2, \cdots, n)$$と置くと、外接円の半径を$R$として $\displaystyle \sum_{k=1}^{n} a_{k}^{2}=(2 n+1) R^{2}$ が成立します。これを証明して $n=3$ とすることで示すこともできます。

本当に正七角形の対角線の比は三角関数を使わないと解けないのですか。