最近はアメリカ大統領選挙のゴタゴタもあり、何かとTrumpが話題ですね。・・・というわけで今回は北大の前期試験からトランプが題材の確率の問題を扱ってみます(笑)。
ジョーカーを除く$1$組$52$枚のトランプのカードを$1$列に並べる試行を考える。
(1)番号$7$のカードが$4$枚連続して並ぶ権率を求めよ。
(2)番号$7$のカードが$2$枚ずつ隣り合い、$4$枚連続しては並ばない確率を求めよ。
(2015年北海道大学 前期文系第4問)
考え方

日本におけるトランプには、スペード、ハート、クラブ、ダイヤの$4$種のスート(suit:一揃い(模様の種類のこと))に分かれており、各スートには$13$の「ランク」(rank:番号)の札があります。トランプの1デッキは模様が$4$種類、数字が$13$種類(数字のみが$10$枚、絵柄付きのJ, Q, Kが$3$枚)の計$52$枚からなります。一応このことは常識の範囲ではありますが、問題文中のどこにも明示されないので予備知識として持っておかなければなりません。
(1)では$4$枚連続したカードをひとかたまりにして考えます。(2)は2枚を一組にして同様に考えます。まず先に$4$枚の番号$7$のカードを除く48枚のカードを並べ、その間に番号$7$のカードの組が入る、というように考えるのが見通し良好です。
文系数学ということもあってか、いかにも教科書に基本問題として載っていそうなタイプの問題です。本問を落とすと一気に差が付くので合格が厳しくなります。確実に仕留めたい問題です。
解答例
まず、全事象は $52!$ 通りであることに注意する。
(1)
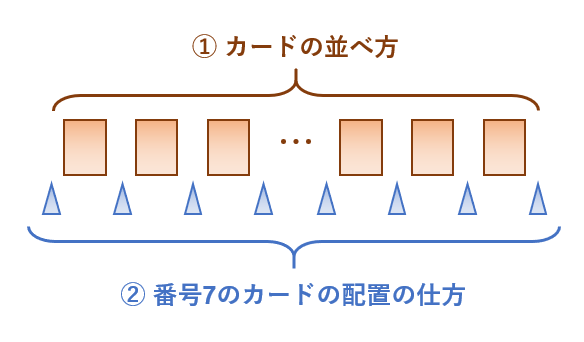
まず、番号$7$以外の48枚のカードを並べる方法①は $48!$ 通りである。
次に$4$枚連続して並んだ番号$7$のカードをひとかたまりにして考えると、$4$枚の並べ方は $4!$ 通りであり、このかたまりを$49$箇所の隙間(上図の青印)のどこに配置するのかで $49$ 通りの方法がある。よって、番号7のカードの配置の仕方②は $4! \cdot 49$ 通りである。
故に求める確率は、$$\begin{align}
& \quad \, \dfrac{48! \cdot (4! \cdot 49)}{52!} \\
&= \dfrac{4 \cdot 3 \cdot 2 \cdot 1}{52 \cdot 51 \cdot 50} \\
&= \dfrac{1}{13 \cdot 17 \cdot 25} \\
&= \color{red}{\dfrac{1}{5525}}
\end{align}$$となる。
(2)
まず、番号$7$以外の48枚のカードを並べる方法①は $48!$ 通りである。

また、番号$7$のカードを2枚をずつ組にして分ける方法が ${}_{4}\mathrm{C}_{2}$ 通り、2組のそれぞれについて並べ方が $2! \cdot 2$ 通り、$49$箇所の隙間のどこを選ぶのかで ${}_{49}\mathrm{C}_{2}$ 通りの方法がある。よって、番号7のカードの配置の仕方②は ${}_{4}\mathrm{C}_{2} \cdot 2! \cdot 2 \cdot {}_{49}\mathrm{C}_{2}$ 通りである。
故に求める確率は、$$\begin{align}
& \quad \, \dfrac{48! \cdot ({}_{4}\mathrm{C}_{2} \cdot 2! \cdot 2 \cdot {}_{49}\mathrm{C}_{2})}{52!} \\
&= \dfrac{48! \cdot \left(\dfrac{4 \cdot 3}{2 \cdot 1} \cdot 2! \cdot 2 \cdot \dfrac{49 \cdot 48}{2 \cdot 1}\right)}{52!} \\
&= \dfrac{4 \cdot 3 \cdot 49 \cdot 48}{52 \cdot 51 \cdot 50 \cdot 49} \\
&= \color{red}{\dfrac{24}{5525}}
\end{align}$$となる。

極めて典型的な確率の問題で、場合の数に慣れていれば確実に得点できます。トランプに限らず「$n$個連続して並ぶ」という事象を考える際は、連続した並びをひとかたまりにして考えるのが定石です。
$n$個連続して並ぶ「?」のかたまりを挿入する場合の数を考えてから、「?」のかたまりの中の並べ方を考える、という数え方のイメージです。もちろん、「?」のかたまりの中の並べ方を数えてから、「?」のかたまりを入れる方法の総数を数える、という手順でも全く同じです。
本問の場合は番号$7$以外の48枚のカードを並べる方法①と番号7のカードの配置の仕方②の積が、すべてのトランプを並べる方法の総数に相当します。これを全事象の総数 $52!$ 通りで割れば確率が求められます。
本問は割と単純な事象の確率を求める問題でしたが、反復試行や条件付き確率も絡めた、より複雑な設定の出題も多く見られます。順列に関する確率の問題に不安がある方は、発展的な類題も含めてよくおさらいしておきましょう。