3次関数が変曲点に関して点対称であることは広く知られています。本稿ではこの事実の証明と、いわゆる3次関数の「4等分の法則」をご紹介します。
3次関数$$y=f(x)=a x^{3}+b x^{2}+c x+d \quad(a \neq 0)$$ の曲線 $C$ は変曲点 $\mathrm{A}\small \left(-\dfrac{b}{3 a}, f\left(-\dfrac{b}{3 a}\right)\right)$ に関して対称になります。
変曲点$\mathrm{A}$が原点にくるように$C$を平行移動した曲線$C’$は$$ \small \begin{align} y &= a\left(x-\frac{b}{3 a}\right)^{3}+b\left(x-\frac{b}{3 a}\right)^{2}+c\left(x-\frac{b}{3 a}\right)+d-f\left(-\frac{b}{3 a}\right) \\ &=ax^3+\left(-\dfrac{b^2}{3a}+c\right)x \end{align}$$と整理できて、奇関数になります。したがって、曲線$C’$は原点に関して対称であることが言えるので、元の曲線 $C$ は変曲点に関して点対称となります。
これより、変曲点に関して対称な接線は平行になります。また当然ながら、2つの接点を結ぶ線分$\mathrm{AB}$の中点は変曲点に一致します。
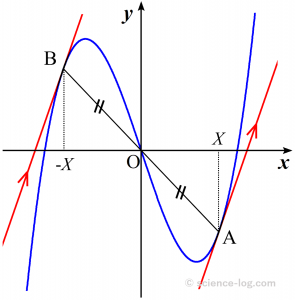
● ● ●
一般に、3次関数は変曲点を原点に合わせるように平行移動すると偶数次の項が消去できます。したがって、3次関数について何らかの性質を示したいときは、奇関数$$y=t x^{3}+u x \quad \cdots(1) \quad(t \neq 0)$$を考えれば十分です($t,u$ は実数)。
この曲線$(1)$上の点 $\left(x_{1},\, t x_{1}^{3}+u x_{1}\right)$($x_{1} \neq 0$)における接線の式は$$y=\left(3 t x_{1}^{2}+u\right)\left(x-x_{1}\right)+t x_{1}^{3}+u x_{1}$$ $$\therefore \quad y=\left(3 t x_{1}^{2}+u\right) x-2 t x_{1}^{3} \quad \cdots (2)$$となります。$(1)$、$(2)$から $y$ を消去すると$$\quad t x^{3}-3 t x_{1}^{2} x+2 t x_{1}^{3}=0$$ $$\therefore \left(x-x_{1}\right)^{2}\left(x+2 x_{1}\right)=0$$ $$\therefore x=x_{1}\ (\text {2重解}), \ -2 x_{1}$$を得ます。
以下に $x_{1}<0$ の場合の図を示します。$x_{1} \neq 0$ の場合、点$\mathrm{P}$で曲線$C$に接する直線は点$\mathrm{Q}$を交点に持ちます。
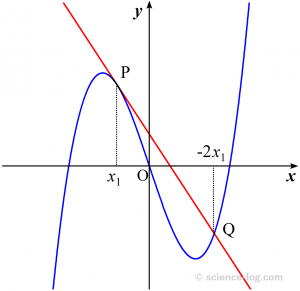
これを応用すると、いわゆる「4等分の法則」を示すことができます。
$y$軸は接点$\mathrm{P}$と交点$\mathrm{Q}$の$x$座標を1:2に分けるので、接点$\mathrm{P}$を極大・極小を与える点に合わせると以下の図のような関係が得られます。
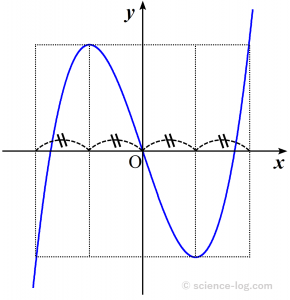
畳が横に4枚(計8枚)並んでいるような見た目ですね。これは極大・極小の存在する3次関数でしか成立しませんが、前もってこの事実を知っていれば、マーク式の問題を解く際や計算結果を検算するときに役立ちます。
3次関数にはこの他にも接線に関する色々な性質があって面白いです。
