2018年の大阪医科大学の前期試験から5次関数の問題を紹介します。
《問題》
$f(x)=\dfrac{1}{27} x^{3}(x-5)^{2}$ とする。
(1)$y=f(x)$ のグラフの概形を、極値を調べて描け。ただし、変曲点は求めなくともよい。
(2)$y=f(x)$ と $y=x$ の共有点はいくつあるか。
(大阪医科大学2018年 前期第1問)
《考え方》
次数が高いですが、微分が使えれば怖くありません。(1)は正しく増減表を掛ければOK、(2)は方程式を解くだけです。(2)では共有点の座標ではなく個数のみ訊かれていますので、中間値の定理を用いた別解も考えられます。
解答例
(1)
$$\small \begin{aligned}
f^{\prime}(x) &=\dfrac{1}{27} \cdot 3 x^{2}(x-5)^{2}+\frac{1}{27} x^{3} \cdot 2(x-5) \\
&=\dfrac{1}{27} x^{2}(x-5)(3(x-5)+2 x\} \\
&=\dfrac{5}{27} x^{2}(x-3)(x-5)
\end{aligned}$$より、増減表は以下のようになる。$$\small \begin{array}{|c||c|c|c|c|c|c|c|}
\hline x & \cdots & 0 & \cdots & 3 & \cdots & 5 & \cdots \\
\hline f^{\prime}(x) & + & 0 & + & 0 & – & 0 & + \\
\hline f(x) & \nearrow & 0 & \nearrow & 4 & \searrow & 0 & \nearrow \\
\hline
\end{array}$$よって、極大値は $f(3)=4$、極小値は $f(5)=0$ であり、グラフの概形は下図のようになる。
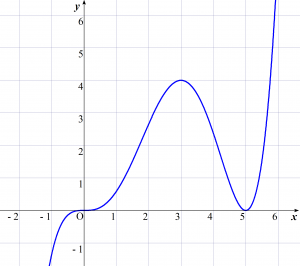
(2)
$y=f(x)$ と $y=x$ を連立すると、$$\small \dfrac{1}{27} x^{3}(x-5)^{2}=x$$ $$\small \therefore x\left\{x^{2}(x-5)^{2}-27\right\}=0$$となる。$x^{2}(x-5)^{2}=27$ のとき $x(x-5)=\pm 3 \sqrt{3}$ となるから、$$\small x^{2}-5 x \mp 3 \sqrt{3}=0$$ $$\small \therefore x=\dfrac{5 \pm \sqrt{25 \pm 12 \sqrt{3}}}{10}$$よって交点は$$\small x=0,\,\dfrac{5 \pm \sqrt{25 \pm 12 \sqrt{3}}}{10}$$と求められるから、共有点は5個である。
(答)5個
(2)別解
$y=f(x)$ と $y=x$ を連立すると、$$\small \dfrac{1}{27} x^{3}(x-5)^{2}=x$$となる。これは5次方程式であるから、この方程式の解の個数は高々5個である。いま、$$\small \begin{array}{l}
f(-1)<-1, \quad f\left(-\dfrac{1}{2}\right)>-\dfrac{1}{2} \\
f(1)<1, \quad f(3)>3 \\
f(5)<5, \quad f(6)>6
\end{array}$$となるから中間値の定理より $-1<x<-\dfrac{1}{2}$、$-\dfrac{1}{2}<x<1$、$1<x<3$、$3<x<5$、$5<x<6$ の区間に少なくとも1つ以上の解が存在している。一方で解の個数は高々5個であるから、共有点は5個と分かる。
(コメント)
5次関数はあまり見かけない気がしたので今回取り上げてみましたが、理系の問題としては易しめですね。文系に出題しても良さそうです。(2)は方程式を解いてしまう方がラクでしょう。
因みに $y=f(x)$ と $y=ax$ は $0<a<\dfrac{625}{432}$ の範囲で5個の共有点を持ちます。
