三角形の重心の存在証明、および、3辺の長さが分かっている三角形の面積を一気に求められる「ヘロンの公式」の証明問題です。珍しい出題なので対策できているかどうかでかなり差が付きそうです。
《問題》
$\triangle \mathrm{ABC}$ について、次の問に答えよ.
(1)辺$\mathrm{BC}$、$\mathrm{CA}$、$\mathrm{AB}$の中点を$\mathrm{D}$、$\mathrm{E}$、$\mathrm{F}$とすると、線分$\mathrm{AD}$、$\mathrm{BE}$、$\mathrm{CF}$は1点$\mathrm{G}$で交わり、$$\mathrm{AG}: \mathrm{GD}=\mathrm{BG}: \mathrm{GE}=\mathrm{CG}: \mathrm{GF}=2: 1$$であることを示せ.
(2)$\triangle \mathrm{ABC}$の面積を$S$、 内接円の半径を$r$、3辺の長さを$a$、$b$、$c$とすると、$$r=\dfrac{S}{l}, \quad S=\sqrt{l(l-a)(l-b)(l-c)}$$であることを示せ.ただし $2l=a+b+c$ とする.
(大阪教育大学2010年 後期第2問)
《考え方》
(1)は重心の存在証明です。中点連結定理を利用します。(2)では面積公式を余弦定理によって式変形し、目的の形まで因数分解していきます。
解答例
(1)
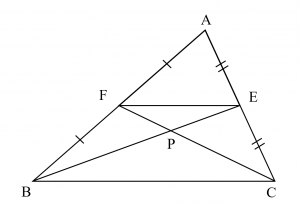
$\triangle \mathrm{ABC}$において中点連結定理より、$$\mathrm{FE} /\!/ \mathrm{BC}, \quad \mathrm{FE}=\dfrac{1}{2} \mathrm{BC}$$であるから、線分$\mathrm{BE}$と線分$\mathrm{CF}$の交点を$\mathrm{P}$するとき、$$\triangle \mathrm{BPC} \sim \triangle \mathrm{EPF}$$であり、$$\begin{align} \mathrm{BP}: \mathrm{PE} &=\mathrm{CP}: \mathrm{PF} \\ &=2: 1 \quad \cdots ①\end{align}$$となる。
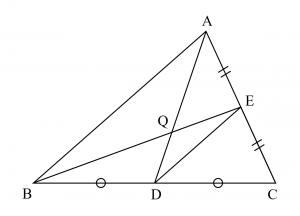
同様に、$$\mathrm{ED} /\!/ \mathrm{AB}, \quad \mathrm{ED}=\dfrac{1}{2} \mathrm{AB}$$であるから、線分$\mathrm{AD}$と線分$\mathrm{BE}$の交点を$\mathrm{Q}$するとき、$$\begin{align} \mathrm{BQ}: \mathrm{QE} &=\mathrm{AQ}: \mathrm{QD} \\ &=2: 1 \quad \cdots ②\end{align}$$となる。
このとき、2点$\mathrm{P}$、$\mathrm{Q}$はいずれも線分$\mathrm{BE}$を$2:1$に内分するから、点$\mathrm{P}$と点$\mathrm{Q}$は一致する。
したがって、この点を$\mathrm{G}$とするとき、線分$\mathrm{AD}$、$\mathrm{BE}$、$\mathrm{CF}$は1点$\mathrm{G}$で交わる。①と②より、$$\begin{align}
\mathrm{A G: G D} &=\mathrm{B G: G E} \\
&=\mathrm{C G: G F} \\
&=2: 1
\end{align}$$である。
□
(2)
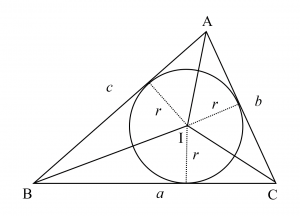
$\triangle \mathrm{ABC}$の内心を$\mathrm{I}$とすると、面積について$$\small \begin{align}
\triangle \mathrm{ABC} &=\triangle \mathrm{IBC}+\triangle \mathrm{ICA}+\triangle \mathrm{IAB} \\
&=\dfrac{1}{2}ar+\dfrac{1}{2}br+\dfrac{1}{2}cr \\
&=\dfrac{1}{2}(a+b+c)r
\end{align}$$が成り立つ。これより、$\triangle \mathrm{ABC}=S$、$2 l =a+b+c$ と置けば $S=lr$ を得る。よって$$\color{red}{r=\dfrac{S}{l}}$$である。
また、面積について$$\begin{align}
S &=\dfrac{1}{2} b c \sin A \\
&=\dfrac{1}{2} b c \sqrt{1-\cos ^{2} A}
\end{align}$$であり、余弦定理から$$\cos A=\frac{b^{2}+c^{2}-a^{2}}{2 b c}$$となるから、$$\small \begin{align}
S &=\frac{1}{2} b c \sqrt{1-\left(\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)^{2}} \\
&=\frac{1}{4} \sqrt{4 b^{2} c^{2}-\left(b^{2}+c^{2}-a^{2}\right)^{2}} \\
&=\frac{1}{4} \sqrt{\left\{2 b c+\left(b^{2}+c^{2}-a^{2}\right)\right\}\left\{2 b c-\left(b^{2}+c^{2}-a^{2}\right)\right\}} \\
&=\frac{1}{4} \sqrt{\left\{(b+c)^{2}-a^{2}\right\}\left\{a^{2}-(b-c)^{2}\right\}} \\
&=\frac{1}{4} \sqrt{(b+c+a)(b+c-a)(a+b-c)(a-b+c)}
\end{align}$$と変形できる。ここで、$2l=a+b+c$ より、$$\begin{cases}
b+c-a=2(l-a) \\
a+b-c=2(l-c) \\
a-b+c=2(l-b)
\end{cases}$$と表せるから、$$\small \begin{align}
S &=\frac{1}{4} \sqrt{2 l \cdot 2(l-a) \cdot 2(l-c) \cdot 2(l-b)} \\
&=\color{red}{\sqrt{l(l-a)(l-b)(l-c)}}
\end{align}$$となる。
□
(コメント)
ヘロンの公式を証明させる問題は稀に出題されるので、対策しておくといざという時に大きなアドバンテージになります。「$\sin$による面積公式を余弦を使う表現に変形してから因数分解する」という手順は覚えておきましょう。ベクトルによる面積公式から求めることも可能ですが、式自体が全く同じものなので手間はほとんど変わりません。
