今週から開催されている「数学夏祭り」の第4問について、問題の背景を独自の視点から考察・解説してみました。
(2020/09/07追記)
この記事が数学夏祭り問4の解説賞に選ばれました!
【問4 解説賞】
数学夏祭り 4日目【確率】@science_log【数学夏祭り】第4問(確率)の面白さについて【2020年夏】https://t.co/QIvyJmrSRW
おめでとうございます!
キャンペーンプライズをお送りします。#数学夏祭り解説 #みんなの推し解説教えて pic.twitter.com/ZtSXaMD3j0— 数学夏祭り@絶賛開催中🎆 (@mathmatsuri) September 7, 2020
第1問についてはこちらから→【数学夏祭り】第一問(整数問題)の解説【2020年夏】
第7’問についてはこちらから→【数学夏祭り】第7’問(関数方程式)について【2020年夏】
【数学夏祭り】第4問
 (数学夏祭り(2020) 第4問)
(数学夏祭り(2020) 第4問)
考え方
解き方に関しては既に多くの人が指摘している通り、基本的には数え上げでゴリ押すしかないでしょう。もちろん、$q=n-p$ が素数になるような組み合わせを効率よく見つける方法はいくつか考えられます。
例えば、偶数$n$それぞれについて素数$p,\,q$を考えるのではなく、表などを作って和が80以下になるような奇素数$p,\,q$の組の個数を調べる方が効率的です。発想の転換ですね。
80以下の奇素数は、
3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79
の22個が存在します。これらから2つの素数$p,\,q$を選び、和 $p+q$ が偶数$n$に一致する組の総数を数えて $n/2$ で割れば$P(n)$が求められます。
また、愚直に数え上げを実行するにしても、$3$以上の奇素数はすべて $6k \pm 1$ の形で表せることを上手く利用しましょう。表を描くにせよグラフを描くにせよ、無駄な筆記や計算は極力避けるよう心掛けるべきです。
本問は力業で解決可能なのでExcel等を使うのが一番手っ取り早いでしょう。今回も例によってPythonのスクリプトを末尾に掲載しておきます*1。シラミ潰しに探索すると、以下のようになります(都合により約分していません)。
P(6) = 1/3 = 0.33333…
P(8) = 2/4 = 0.5
P(10) = 3/5 = 0.6
P(12) = 2/6 = 0.33333…
P(14) = 3/7 = 0.42857…
P(16) = 4/8 = 0.5
P(18) = 4/9 = 0.44444…
P(20) = 4/10 = 0.4
P(22) = 5/11 = 0.45454…
P(24) = 6/12 = 0.5
P(26) = 5/13 = 0.38461…
P(28) = 4/14 = 0.28571…
P(30) = 6/15 = 0.4
P(32) = 4/16 = 0.25
P(34) = 7/17 = 0.41176…
P(36) = 8/18 = 0.44444…
P(38) = 3/19 = 0.15789…
P(40) = 6/20 = 0.3
P(42) = 8/21 = 0.38095…
P(44) = 6/22 = 0.27272…
P(46) = 7/23 = 0.30434…
P(48) = 10/24 = 0.41666…
P(50) = 8/25 = 0.32
P(52) = 6/26 = 0.23076…
P(54) = 10/27 = 0.37037…
P(56) = 6/28 = 0.21428…
P(58) = 7/29 = 0.24137…
P(60) = 12/30 = 0.4
P(62) = 5/31 = 0.16129…
P(64) = 10/32 = 0.3125
P(66) = 12/33 = 0.36363…
P(68) = 4/34 = 0.11764…
P(70) = 10/35 = 0.28571…
P(72) = 12/36 = 0.33333…
P(74) = 9/37 = 0.24324…
P(76) = 10/38 = 0.26315…
P(78) = 14/39 = 0.35897…
以上より、$P(n)$が最小となるのは$$\color{red}{n=68}$$であり、このとき$$\color{red}{P(68)=\dfrac{2}{17}}$$と求められます。機械の力に頼らずに求める場合はシラミ潰しでも良いですが、もう少し工夫してスマートに解答しましょう。
以下、本問の背景について解説します。
グラフによる考察
この問題設定で $n=100$ までを考えると、$P(n)$のグラフ(青色の折れ線グラフ)は以下のようになります。横軸が$n$、縦軸が$P(n)$です。
確かに $n=68$ で最小(極小)になっていることが見て取れますね。
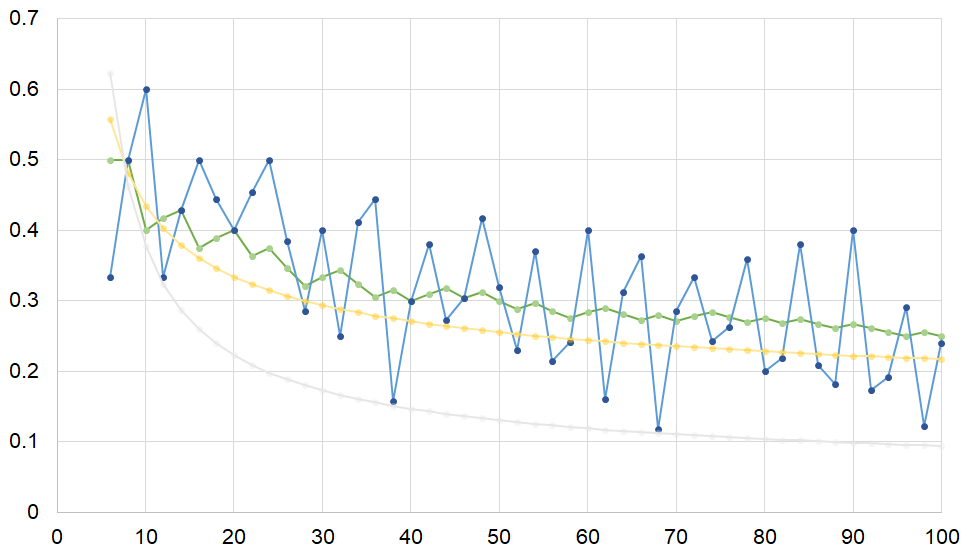
緑色の折れ線は $\dfrac{\pi(n)}{n}$($\pi(n)=$「$n$を超えない素数の個数」)、黄色の曲線が $\dfrac{1}{2\ln n}$、灰色の曲線が $\dfrac{2}{(\ln n)^2}$ を表しています。ここで、$\ln n$ は自然対数 $\log_e n$ と同じものです。
$P(n)$のグラフは乱雑に波打っていて、ここから何らかの規則性を導き出すのは難しそうですね。このグラフを見ると、本問に対しては効率的な解法が無さそうであることが直感できます。
ところで、この問題を一般化するとどうなるのでしょうか? 本問では$80$が$n$の上限ですが、もっと広い範囲で考えてみます。
$n=1000$ までの範囲では$P(n)$のグラフは次のようになります。濃い黄色の曲線は $\dfrac{1}{\ln n}$ のグラフです。
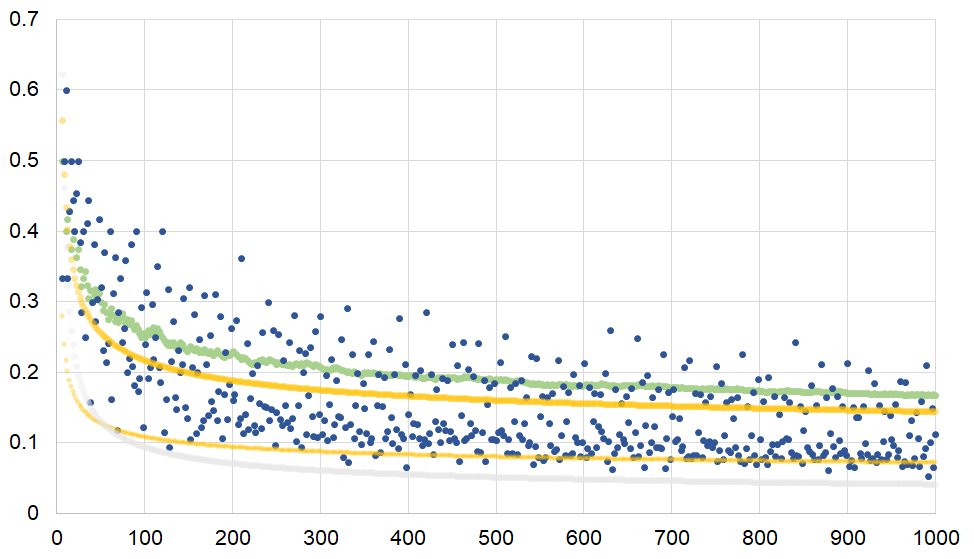
何となくプロットが2層に分かれているように見えます。
さらに $n=10000$ まで範囲を拡げると、$P(n)$のグラフは次のようになります。薄桃色の曲線は $\dfrac{2}{(\ln n)^2}$ のグラフです。
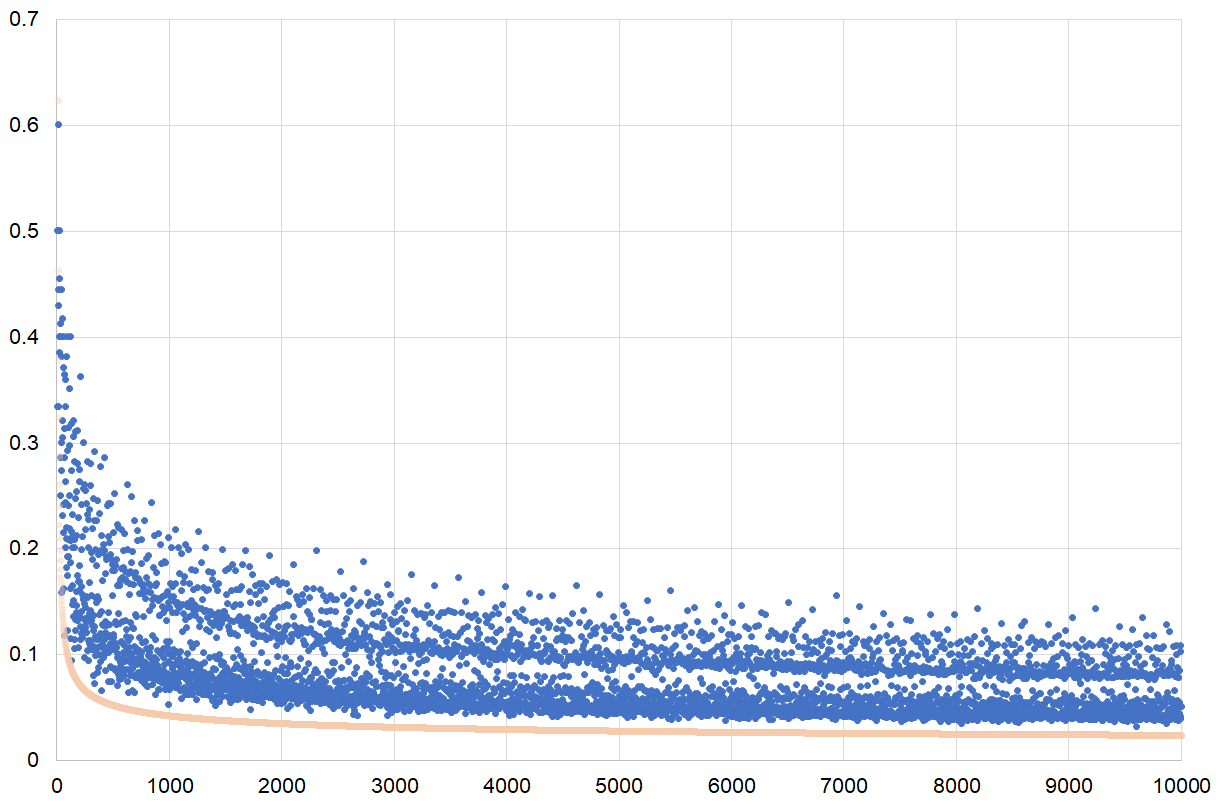
これを見ると分かるように、どうやら$P(n)$の値は$n$によって2つの層に分けられそうです。上の層は$P(n)$が大きい、つまり$p,\,q$の組が素数になりやすいことを意味しており、下の層では$p,\,q$の組が素数になりにくいことを意味しています。
ゴールドバッハ予想と素数定理
ところで、偶数と素数に関する命題としては次のものが有名です。
「$2$より大きいすべての偶数は、$2$つの素数の和となる」
これを「ゴールドバッハ予想」と言います。ゴールドバッハ(1690~1764)はプロイセン東部(現在のカリーニングラード)出身の数学者で、有名な数学者であるオイラーなどとも交流していました。ゴールドバッハはオイラーとの書簡のやり取りの中で上記の予想について触れていますが、この予想は当時から今に至るまで誰にも証明されておらず、数論の未解決問題として現代でも盛んに研究されているテーマです。
なぜいきなりゴールドバッハ予想が出てくるのかと言うと、実は今回の第4問の背景にはこの予想が隠れているからです。今回取り組んだ方の中にはゴールドバッハ予想との関連性に気が付いた方も多かったのではないでしょうか。
そして、問題文ではあからさまには触れられていませんが、この問題で重要となるもう一つのポイントは「素数の数とその分布」です。
素数の分布についてはガウスやルジャンドルによって予想された「素数定理」というものが知られています。これは要するに$x$以下の素数の数を$\pi (x)$とすると$$\pi (x) \approx \dfrac {x}{\ln x}$$と近似できるというもので、これにより$x$以下の範囲におおよそ $\dfrac {1}{\ln x}$ の割合で素数が存在することが導かれます。
これを既知とすると、$m$ と $n-m$ が同時に素数になる確率は一般に、$$\dfrac{1}{\ln m} \dfrac{1}{\ln (n-m)}$$と近似的に表せるので、$m\,(\leqq n/2)$ について和をとると $m$ と $n-m$ が同時に素数になるような場合の数は$$\displaystyle \sum_{m=3}^{n / 2} \dfrac{1}{\ln m} \dfrac{1}{\ln (n-m)} \approx \dfrac{n}{2(\ln n)^{2}}$$と近似できます。これより、そのような組が存在する割合、つまり今回の確率$P(n)$は$$P(n) \approx \dfrac{1}{2(\ln n)^{2}}$$と近似できます。
※ ここで、$m$ と $n-m$ が素数になること自体は独立な事象ではないので、確率が積の形になるという仮定は厳密には不正確であることに注意して下さい。以上の議論は$n$が十分大きい場合ではある程度妥当と言えます。
理論的には $P(n) \approx \dfrac{1}{2(\ln n)^{2}}$ なのですが、やはり近似の精度が悪く、この式は$P(n)$をかなり過小評価してしまいます。そこで少し調べてみると、$4$倍した $\dfrac{2}{(\ln n)^{2}}$ だと$P(n)$を下から上手く押さえられることが分かります。実際、$n=10000$ までのグラフを見ても、上手く$P(n)$を評価できていることが観察できます。
※ $n=68$ とすると$$\dfrac{2}{(\ln n)^{2}} \approx 0.112332…$$となり、$\dfrac{2}{17}=0.117647…$ とかなり近い値になっています。ただしこれはどちらかというと偶然に近い気もしますが…。
最後にプロットの分布について触れておきます。
「ゴールドバッハの彗星」
皆さんは「ゴールドバッハの彗星」というものを聞いたり目にしたりしたことがあるでしょうか?
横軸を「正の偶数$n$」、縦軸を「$n$を2つの奇素数の和に分割する方法の数 $g(n)$(Goldbach Partition*2)」としてプロットしたグラフは以下のようになります。点の分布の様子が「ほうき星」に似ていることから、「ゴールドバッハの彗星(Goldbach’s comet)」と呼ばれています。
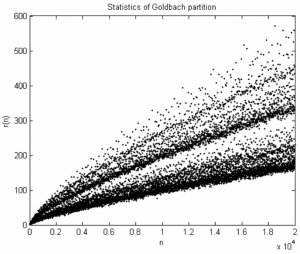 ゴールドバッハの彗星
ゴールドバッハの彗星
(”Fractal in the statistics of Goldbach partition” より引用)
ゴールドバッハの彗星はプロットが幾つかの層に分かれて見えるのが特徴で、これらの層は偶数$n$の剰余類と関係があります。実は今回の$P(n)$のプロットもこれに類似したプロットになっています。
$n=10000$ までの確率$P(n)$のグラフについて、$n$を$3$で割った余りが$0$のときは赤、$1$のときは青、$2$のときは緑として再度プロットすると以下のようになります。
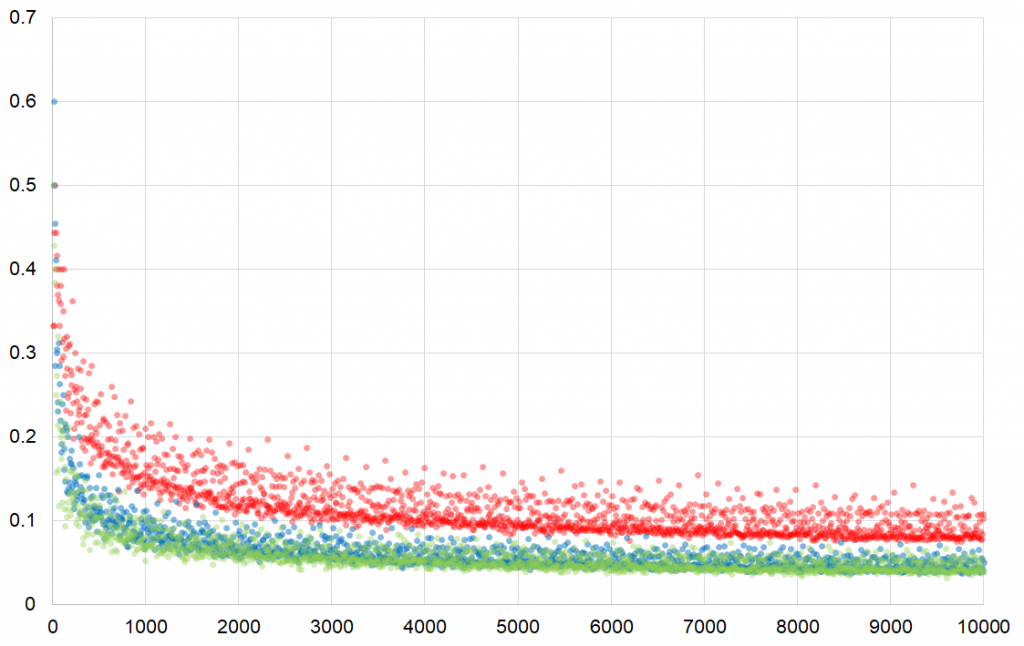
見事に層がくっきり分かれているのが見て取れます。$n$が大きくなるにつれて混みあっていて見にくいので逆数をとると、次のようになります。
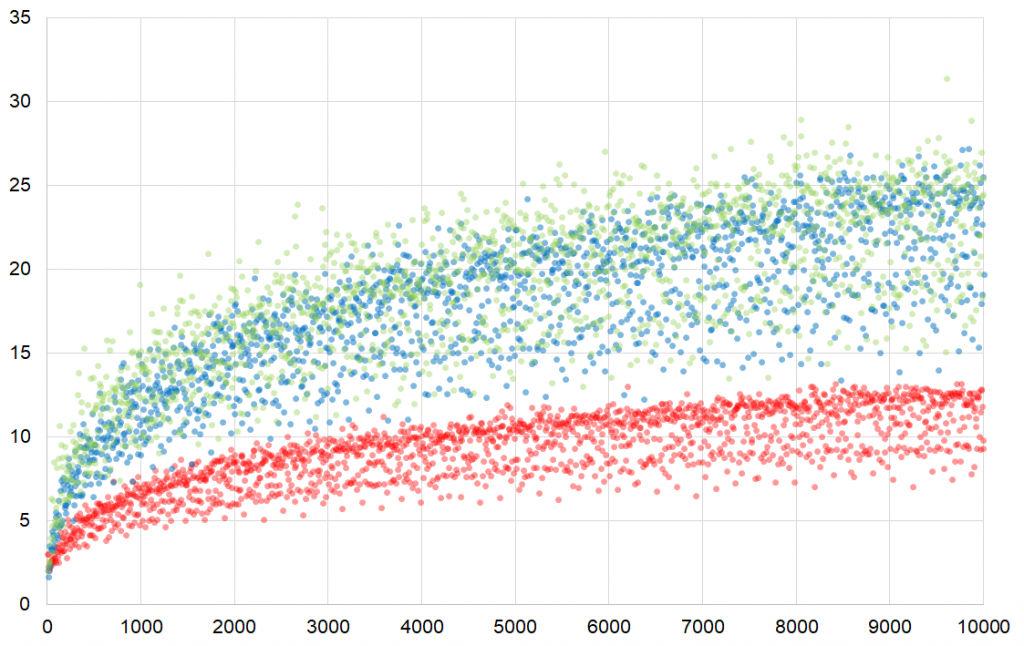
本家のゴールドバッハの彗星とは縦軸のオーダーが異なりますが、$\dfrac{1}{P(n)}$ のグラフでも同様に「ほうき星」のような形になっています。綺麗ですね!
$n=100$ までのグラフからは規則性が全く見えませんでしたが、このグラフからは、偶数$n$を$3$で割った余りが$0$のとき(赤)は$P(n)$が大きくなりやすく、$3$で割った余りが$2$のとき(緑)は$P(n)$が小さくなりやすいことが定性的に言えそうです。実際に、第4問の答えとなった $n=68$ は$3$で割った余りが$2$となる整数です。
ゴールドバッハの彗星でも、分割数$g(n)$が小さくなる傾向があるのは$3$で割った余りが$2$となる偶数$n$の場合です。つまり、$n \equiv 2 \pmod{3}$ となるときは $n=p+q$ と表せる奇素数$p,\,q$の組が少なくなるので、当然 $n-p\,(=q)$ が素数となるような素数$p$の数も少なくなり、結果的に本問の$P(n)$に相当する確率(というよりこの場合は「割合」と言った方が適切かもしれません)が小さくなるのです。
というわけで、今回の確率の問題は「ゴールドバッハ予想」や「素数定理」が背景にある問題だったのでした。
ここまで色々と紹介してきた内容は、問題を解く上ではそれほど役に立たない知識かもしれませんが、問題の背景を理解すれば「単なる数え上げのつまらない問題」から「数学の奥深い所からやってきたキュートな問題」に見方が変わるはずです。そういった広がりのある楽しみを提供するのも作問者や解説者の使命の一つなのだと思います。
今回の問題やこの記事が少しでも皆さんの数学心に響いたら幸いです。最後までお読み頂きありがとうございました!
先ほど$P(n)$を分数表示したときに約分していませんでしたが、実は分子の値はオンライン整数列辞典OEISのA035026として登録されています。これは$2n$を2つの奇数素数の和に分解する方法の総数A002372と関わりが深い(というかほとんど同じ)数列であり、今回の第4問はゴールドバッハ予想に造詣の深い方が作問されたのではないかと思います。
「数学夏祭り」も今日で5日目。本日は解析分野から難問が出るらしいので楽しみですね!
*1 Pythonを使えば以下のようなプログラムで組み合わせが全通り求められ、確率$P(n)$が計算できます。
p = [2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83]
N = 3
while 2*N <= 80:
i = 0
times = 0
while i <= len(p) and p[i] <= 2*N:
if 2*N-p[i] in p:
times = times + 1
i = i + 1
print("P("+str(2*N)+") = ",times," /",N," = ",times/N)
N = N + 1
*2 偶数$n$を2つの奇素数の和に分割する方法の数 $g(n)$ は “Goldbach Partition” と呼ばれる数列で、今回の確率$P(n)$について$$P(n)=\dfrac{g(n)}{n/2}$$が成り立ちます。$g(n)$ は $\dfrac{n}{(\ln n)^2}$ のオーダーをもつため、$P(n)$ は $\dfrac{1}{(\ln n)^2}$ のオーダーとなることが言えます。これは上記のグラフで確認した通りですね。

“【数学夏祭り】第4問(確率)の面白さについて【2020年夏】” への2件の返信