「正方形の頂点を結ぶ最短のグラフは何か」という最小シュタイナー木問題が背景にある問題です。本問は数Ⅲの知識で解答可能です。
《問題》
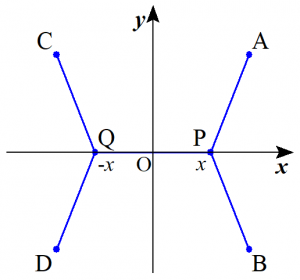
座標平面に4点$\mathrm{A}(1,1)$、$\mathrm{B}(1,-1)$、$\mathrm{C}(-1,1)$、$\mathrm{D}(-1,-1)$がある。実数$x$が $0 \leqq x \leqq 1$ の範囲にあるとき、2点$\mathrm{P}(x,0)$、$\mathrm{Q}(-x,0)$を考える。このとき、5本の線分の長さの和$$\mathrm{AP}+\mathrm{BP}+\mathrm{PQ}+\mathrm{CQ}+\mathrm{DQ}$$が最小となるような$x$の値を求めよ。ただし、$x=0$ のときは $\mathrm{PQ}=0$ とする。
(早稲田大学2015年 教育(理系)第1問(2))
《考え方》
5本の線分の長さの和を$x$の関数で表し、微分法で最小値を求めましょう。$x=\sin \theta$($0 \leqq \theta \leqq \dfrac{\pi}{2}$)などと置いても良いですが、結局数Ⅲの微分法は必要になります。
● ● ●
解答例
$$\small \begin{align}
& \quad \ \mathrm{AP}+\mathrm{BP}+\mathrm{PQ}+\mathrm{CQ}+\mathrm{DQ} \\
&=2(\mathrm{OP}+2 \mathrm{PA}) \\
&=2\{x+2 \sqrt{(x-1)^{2}+1}\}
\end{align}$$ここで $f(x)=x+2 \sqrt{(x-1)^{2}+1}$ と置くと、$$\small \begin{aligned}
f^{\prime}(x) &=1+2 \cdot \frac{2(x-1)}{2 \sqrt{(x-1)^{2}+1}} \\
&=\frac{\sqrt{(x-1)^{2}+1}-2(1-x)}{\sqrt{(x-1)^{2}+1}}
\end{aligned}$$見やすさのために $t=\sqrt{(x-1)^{2}+1}$ と置き換えると、$$\small \begin{aligned}
f^{\prime}(x) &=\frac{(x-1)^{2}+1-4(1-x)^{2}}{t\{t+2(1-x)\}} \\
&=\frac{1-3(1-x)^{2}}{t\{t+2(1-x)\}} \\
&=\frac{\{1-\sqrt{3}(1-x)\}\{1+\sqrt{3}(1-x)\}}{t\{t+2(1-x)\}}
\end{aligned}$$となる。
$1-x>0$、$t+2(1-x)>0$ であることに注意する。ここで、$1-\sqrt{3}(1-x)=0$ のとき $x=1-\dfrac{1}{\sqrt{3}}$ であり、
$1-\sqrt{3}(1-x)<0$ のとき、つまり $0<x<1-\dfrac{1}{\sqrt{3}}$ のとき、$f^{\prime}(x)<0$となり、
$1-\dfrac{1}{\sqrt{3}}<x<1$ のとき $f^{\prime}(x)>0$ となる。
よって、増減表は次のようになる。$$\begin{array}{|c||c|c|c|c|c|}
\hline x & 0 & \cdots & \small{1-\dfrac{1}{\sqrt{3}}} & \cdots & 1 \\
\hline f^{\prime}(x) & & – & 0 & + & \\
\hline f(x) & & \searrow & & \nearrow & \\
\hline
\end{array}$$よって$f(x)$は$$x=\color{red}{1-\dfrac{1}{\sqrt{3}}}$$のとき最小となる。
(※5本の線分の長さの和の最小値は $2(1 + \sqrt{3}\,)$)
(コメント)
本問は最小シュタイナー木問題が背景にある問題です。 これは最短連結問題や最短ネットワーク問題などと呼ばれることがあります。与えられた幾つかの点をすべて連結させるグラフを考えます。ここで言う「グラフ」というのは「$y=f(x)$ のグラフ」といった意味ではなく、点(ノード)を直線や曲線(エッジ)で結んだ「木」(tree) というグラフ理論的な意味の用語です。本問の場合は正方形の各頂点$\mathrm{A}$~$\mathrm{D}$と内部の点$\mathrm{P}$、$\mathrm{Q}$が「ノード」、これらを結ぶ5本の線分が「エッジ」に対応します(※内部の点$\mathrm{P}$、$\mathrm{Q}$は元々自明に存在する点ではなく、これらは最小シュタイナー木に新たに追加された点(シュタイナー点)であり、わざとノードに含めないこともあります)。
正方形の最小シュタイナー木は上記で見たような図形となります。何のヒントも与えられていない場合だと、単純に対角線が最小の連結グラフになる気がしてしまいますが、実はそうではありません。1辺が$1$の正方形の2本の対角線は $2\sqrt{2} \approx 2.828$ であり、先ほど求めた5本の線分からなる木の全長は $1+\sqrt{3} \approx 2.732$ となるからです。
三角形の場合の最小シュタイナー木は、フェルマー点と各頂点をつなぐ線分となります。これを題材とした問題が2013年の東大理科第4問に出題されています。
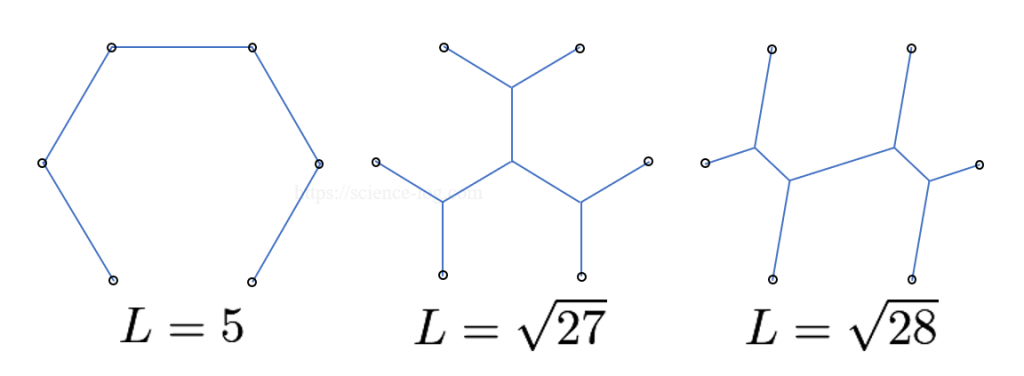
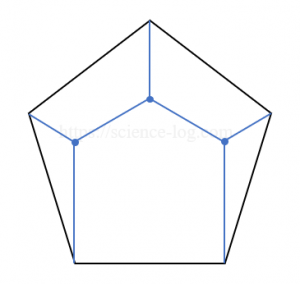
また、正5角形の場合は以下のようになります。この全長を解析的に求められるのかについては寡聞にして知りません。
正6角形の場合は以下のようになります。正$n$角形($n$は$6$以上)では最小シュタイナー木の全長は $n-1$ となり、内部にシュタイナー点を取るよりも周を辿る方が経路が短くなることが知られています。