本稿では化学反応の議論する上で重要となる反応速度論の知識について整理する。速度論の内容は大学教養レベルの数学を含んでいるが、高校生でも理解できるように解説していく。
§化学反応のダイナミクス
化学反応を解析する際、濃度や結合様式、平衡などが考慮されるが、時間という因子を考慮するときに速度論の知識が必要となる。化学反応は一般にある一定の方向に進行するが、それは組成の割合が常に一定ということを意味しない。化学反応の平衡定数が分かっていても反応の進み方が分かる訳ではなく、あくまでも反応の「行き先」の見当が付くというだけに過ぎない。実際の反応においては時々刻々と組成の割合が変化しており、一般的な反応の時間的な追跡は容易ではない。次のような簡単な反応でも微分方程式に関する知識が必要となり、速度論的な解析には数学の知識が必要となる。$$\mathrm{A} \overset{k}{\to} \mathrm{P}$$これは、反応物分子$\mathrm{A}$が一定の確率で生成物分子$\mathrm{P}$に変化する反応である。これが逐次反応や逆反応を考慮しなければならない系になると濃度の時間変化の複雑さはより一層増していく。
§反応速度の定義
ここで反応速度の定義についておさらいしておこう。$$\alpha\,\mathrm{A}+\beta\,\mathrm{B} \rightleftarrows \gamma\,\mathrm{C}+\delta\,\mathrm{D}\tag{1.1}$$この化学反応に対する正反応の速度$R_f$は以下のように表すことができる。$$R_f=k_f[\mathrm{A}]^{\alpha}[\mathrm{B}]^{\beta}\tag{1.2}$$ここで$k_f$は比例定数である。逆反応の速度$R_b$は同様に以下のように表すことができる。$$R_b=k_b[\mathrm{C}]^{\gamma}[\mathrm{D}]^{\delta}\tag{1.3}$$したがって$(1.1)$の化学反応における全体の反応速度$r$は$$\begin{align} r &=R_f-R_b \\ &=k_f[\mathrm{A}]^{\alpha}[\mathrm{B}]^{\beta}-k_b[\mathrm{C}]^{\gamma}[\mathrm{D}]^{\delta} \tag{1.4}\end{align}$$と表すことができる。化学平衡とは正反応の速度と逆反応の速度が釣り合って見かけ上反応が進まない状態を意味するから、$(1.4)$式より、平衡においては$$k_f[\mathrm{A}]^{\alpha}[\mathrm{B}]^{\beta}-k_b[\mathrm{C}]^{\gamma}[\mathrm{D}]^{\delta}=0$$ $$\therefore \dfrac{k_f}{k_b}=\dfrac{[\mathrm{C}]^{\gamma}[\mathrm{D}]^{\delta}}{[\mathrm{A}]^{\alpha}[\mathrm{B}]^{\beta}} \tag{1.5}$$という関係が成り立つ。$(1.5)$式はある定数であり、この定数こそが「平衡定数$K$」と呼ばれているものの正体である。要するに平衡定数とは正反応の反応速度定数$k_f$と逆反応の反応速度定数$k_b$の比である。これより、平衡定数を求めるには$k_f$と$k_b$が分かっていればよいことが理解できる。
§反応速度の導出(一次反応)
それでは早速、冒頭で紹介した一次反応の例で反応速度を考察してみよう。$$\mathrm{A} \overset{k}{\to} \mathrm{P} \tag{2.1}$$この反応は$\mathrm{A}$がある一定の確率で生成物$\mathrm{P}$に変化する反応で、反応速度は反応物$\mathrm{A}$の濃度にのみ依存する。以下の図は分かりやすくするために1原子分子としているのでイメージ図に過ぎないが、逆反応を考えない限り反応速度は$\mathrm{A}$の濃度$[\mathrm{A}]$のみで記述できる。
この反応全体の速度は反応物$\mathrm{A}$の消費速度に等しいことから、以下の微分方程式が成立する。$$-\dfrac{d[\mathrm{A}]}{dt}=k[\mathrm{A}]\tag{2.2}$$「消費速度」なので負号を付ける必要があることに注意しよう。また、あらわに表記してはいないが、ここで$[\mathrm{A}]$は時刻$t$の関数となっている。
さて、これは標準的な変数分離型の微分方程式である。以下のような式変形で解を求めることができる。$$\dfrac{1}{[\mathrm{A}]}d[\mathrm{A}]=-k\,dt\tag{2.3}$$ $$\therefore \int^{[\mathrm{A}]}_{[\mathrm{A}]_0} \dfrac{1}{[\mathrm{A}]}d[\mathrm{A}]=-k\int^{t}_{0}dt\tag{2.4}$$ $$\therefore \ln\dfrac{[\mathrm{A}]}{[\mathrm{A}]_{0}} =-kt\tag{2.5}$$ $\ln$は高校生にとっては見慣れないかもしれないが、自然対数 $\log_e$ の略記である。化学のみならず科学全般においては自然対数を$\ln$、常用対数を単に$\log$と書く習慣がある。この辺りは高校数学の記法と混同する恐れがあるので要注意である。
$(2.5)$式の対数を外して、$$\dfrac{[\mathrm{A}]}{[\mathrm{A}]_{0}}=e^{-kt}\tag{2.6}$$ $$\therefore [\mathrm{A}]=[\mathrm{A}]_{0}e^{-kt}\tag{2.7}$$を得る。生成物$\mathrm{P}$の初濃度を$0$とすれば関係式$$[\mathrm{A}]+[\mathrm{P}]=[\mathrm{A}]_{0}\tag{2.8}$$が常に成立するから、時刻$t$における生成物$\mathrm{P}$の濃度$[\mathrm{P}]$は$$\begin{align}[\mathrm{P}] &=[\mathrm{A}]_{0}-[\mathrm{A}] \\ &=[\mathrm{A}]_{0}(1-e^{-kt}) \tag{2.9}\end{align}$$と求められる。青線を$[\mathrm{A}]$、赤線を$[\mathrm{P}]$として時刻に関してプロットすると以下のようになる。
この場合、反応物$\mathrm{A}$の半減期$\tau_{1/2}$は$(2.7)$式を用いて$$[\mathrm{A}]=\dfrac{1}{2}[\mathrm{A}]_{0}\tag{2.10}$$を解くことにより$$\tau_{1/2}=\dfrac{1}{2k[\mathrm{A}]_{0}}\tag{2.11}$$と求められる。なお、反応物や生成物の濃度の時間追跡が正確に行えるのであれば半減期だけを特別視する必要は無く、反応物$\mathrm{A}$の濃度が$\dfrac{1}{e}$に減少する時間を化学種$\mathrm{A}$の「寿命」(life time)或いは「時定数」(time constant)と呼び、$\tau$と書く。上記のような一次反応であれば$\tau$は反応速度定数の逆数で表される($(2.12)$式)。$$\tau=\dfrac{1}{k}\tag{2.12}$$一次反応でなくても反応速度定数の逆数は反応速度の比を見積もる目安として利用されることが多い。
§反応速度の導出(二次反応)
次に$$2\mathrm{A} \overset{k}{\to} \mathrm{P} \tag{3.1}$$と書き表せる反応について調べてみよう。これは2分子の$\mathrm{A}$がある一定の確率で出会うことで生成物$\mathrm{P}$に変化する反応と解釈でき、逆反応を考えない限り反応速度は一次反応と同様、$\mathrm{A}$の濃度$[\mathrm{A}]$のみで記述できる。
この反応では左辺と右辺で物質量が変わるのでやや難しく感じられるかもしれない。反応物$\mathrm{A}$の消費速度に関する微分方程式を立てることができれば後は計算するだけでよいから、まずは微分方程式を正しく立式することが目標となる。
反応には2分子の$\mathrm{A}$が必要となるから、微分方程式は$$-\dfrac{d[\mathrm{A}]}{dt}=2k[\mathrm{A}]^2\tag{3.2}$$となる。ここで、右辺を単に$k[\mathrm{A}]^2$としてしまわないように気を付けよう。1回の反応につき$\mathrm{A}$は2分子消費されるので、$2$を乗じる必要がある。
$(3.2)$の微分方程式は同様に変数分離により解を求めることができる。$$-\dfrac{1}{[\mathrm{A}]^2}d[\mathrm{A}]=2k\,dt\tag{3.3}$$ $$\therefore -\int^{[\mathrm{A}]}_{[\mathrm{A}]_{0}} \dfrac{1}{[\mathrm{A}]^2}d[\mathrm{A}]=2k\int^{t}_{0}dt\tag{3.4}$$ $$\therefore \dfrac{1}{[\mathrm{A}]}-\dfrac{1}{[\mathrm{A}]_{0}} =2kt\tag{3.5}$$ $$\therefore [\mathrm{A}]=\dfrac{[\mathrm{A}]_{0}}{1+2k[\mathrm{A}]_{0}t}\tag{3.6}$$を得る。生成物$\mathrm{P}$の初濃度を$0$とすれば、化学反応の量論比より、関係式$$[\mathrm{P}]=\dfrac{1}{2}([\mathrm{A}]_{0}-[\mathrm{A}])\tag{3.7}$$が常に成立するから、時刻$t$における生成物$\mathrm{P}$の濃度$[\mathrm{P}]$は$$\begin{align}[\mathrm{P}] &=\dfrac{1}{2}([\mathrm{A}]_{0}-[\mathrm{A}]) \\ &=\dfrac{[\mathrm{A}]_{0}}{2}\left(1-\dfrac{1}{1+2k[\mathrm{A}]_{0}t}\right) \tag{3.8}\end{align}$$と求められる。青線を$[\mathrm{A}]$、赤線を$[\mathrm{P}]$として時刻に関してプロットすると以下のようになる。
ここで、$[\mathrm{A}]_{0}=1$、$k=1$ として$[\mathrm{A}]$の時間変化を一次反応と二次反応で比較してみると、一次反応では$$[\mathrm{A}]=e^{-t}\tag{3.9}$$となり、二次反応では$$[\mathrm{A}]=\dfrac{1}{1+2t}\tag{3.10}$$となる。これを同じ $t$-$[\mathrm{A}]$ 平面にプロットすると以下のようになる。
青線が一次反応($(3.9)$式)、紫線が二次反応($(3.10)$式)である。反応初期は二次反応の方がよく進行し、$\mathrm{A}$の濃度が減少していくと二次反応よりも一次反応の方がよく進行することが知られているが、この現象は速度論により数学的に説明することができるのである。
§反応速度の導出(一般の二次反応)
最後に$$\mathrm{A}+\mathrm{B} \overset{k}{\to} \mathrm{P} \tag{4.1}$$と書き表せる反応について調べてみよう。これはそれぞれ1分子の$\mathrm{A}$と$\mathrm{B}$がある一定の確率で出会うことで生成物$\mathrm{P}$に変化する反応と解釈できる。逆反応を考えない限り、反応速度は2分子の$\mathrm{A}$の場合と同様、濃度$[\mathrm{A}]$、$[\mathrm{B}]$を含む二次の項で記述できる。
したがって反応物$\mathrm{A}$の消費速度に関する微分方程式は$$-\dfrac{d[\mathrm{A}]}{dt}=k[\mathrm{A}][\mathrm{B}]\tag{4.2}$$となる。$\mathrm{A}$、$\mathrm{B}$の消費速度は等しいと仮定できるので、ある時刻$t$における$\mathrm{A}$の濃度と$\mathrm{B}$の濃度は常に一致する。これより関係式$$[\mathrm{A}]_{0}-[\mathrm{A}]=[\mathrm{B}]_{0}-[\mathrm{B}]\tag{4.3}$$が導かれる。$(4.3)$式より、$(4.2)$式の$[\mathrm{B}]$を消去すると$$-\dfrac{d[\mathrm{A}]}{dt}=k[\mathrm{A}]([\mathrm{A}]-[\mathrm{A}]_{0}+[\mathrm{B}]_{0})\tag{4.4}$$を得る。
$[\mathrm{A}]_{0}=[\mathrm{B}]_{0}$ のときは$(3.2)$式に一致して同様に計算できるので、$[\mathrm{A}]_{0} \ne [\mathrm{B}]_{0}$ のときを考えよう。$(4.4)$式は$$\dfrac{d[\mathrm{A}]}{[\mathrm{A}]([\mathrm{A}]-[\mathrm{A}]_{0}+[\mathrm{B}]_{0})}=-k\,dt\tag{4.5}$$ $$\therefore \left(\dfrac{1}{[\mathrm{A}]}-\dfrac{1}{[\mathrm{A}]-[\mathrm{A}]_{0}+[\mathrm{B}]_{0}}\right)\dfrac{d[\mathrm{A}]}{[\mathrm{B}]_{0}-[\mathrm{A}]_{0}}=-k\,dt\tag{4.6}$$と変形できるので、これを両辺積分して、$$\therefore \ln\dfrac{[\mathrm{A}]}{[\mathrm{A}]_{0}}-\ln\dfrac{[\mathrm{A}]-[\mathrm{A}]_{0}+[\mathrm{B}]_{0}}{[\mathrm{B}]_{0}}=-([\mathrm{B}]_{0}-[\mathrm{A}]_{0})kt\tag{4.7}$$を得る。これを$[\mathrm{A}]$について整理すると$$[\mathrm{A}]=\dfrac{[\mathrm{A}]_{0}([\mathrm{A}]_{0}-[\mathrm{B}]_{0})}{[\mathrm{A}]_{0}-[\mathrm{B}]_{0}e^{^{([\mathrm{B}]_{0}-[\mathrm{A}]_{0})kt}}}\tag{4.8}$$と求められる。よって生成物$\mathrm{P}$の初濃度が$0$のとき、$\mathrm{P}$の濃度は$$[\mathrm{P}]=[\mathrm{A}]_{0}\left(1-\dfrac{[\mathrm{A}]_{0}-[\mathrm{B}]_{0}}{[\mathrm{A}]_{0}-[\mathrm{B}]_{0}e^{^{([\mathrm{B}]_{0}-[\mathrm{A}]_{0})kt}}}\right)\tag{4.9}$$で与えられる。これは$$[\mathrm{P}]=[\mathrm{A}]_{0}[\mathrm{B}]_{0}\left(\dfrac{1-e^{^{([\mathrm{B}]_{0}-[\mathrm{A}]_{0})kt}}}{[\mathrm{A}]_{0}-[\mathrm{B}]_{0}e^{^{([\mathrm{B}]_{0}-[\mathrm{A}]_{0})kt}}}\right)\tag{4.10}$$と書き直してもよい。これより、最終的な$\mathrm{P}$の濃度は$\displaystyle \lim_{t \to \infty}e^{^{([\mathrm{B}]_{0}-[\mathrm{A}]_{0})kt}}$の極限の値によって決まることが分かる。$[\mathrm{A}]_{0}<[\mathrm{B}]_{0}$ のときは $\displaystyle \lim_{t \to \infty}e^{^{([\mathrm{B}]_{0}-[\mathrm{A}]_{0})kt}}=\infty$ なので $[\mathrm{P}] \to [\mathrm{A}]_{0}$ が成り立ち、$[\mathrm{A}]_{0}>[\mathrm{B}]_{0}$ のときは $\displaystyle \lim_{t \to \infty}e^{^{([\mathrm{B}]_{0}-[\mathrm{A}]_{0})kt}}=0$ なので $[\mathrm{P}] \to [\mathrm{B}]_{0}$ が成り立つことが分かる。
※$(4.9)$式や$(4.10)$式は見掛けからは判断しにくいが、実際は2つの定数$[\mathrm{A}]_{0}$、$[\mathrm{B}]_{0}$に関して対称な式である。反応式$(4.1)$においては特に$\mathrm{A}$、$\mathrm{B}$を区別していないので、$[\mathrm{P}]$の式は対称式となる必要がある。
また、$[\mathrm{A}]_{0}\ll[\mathrm{B}]_{0}$ のときは$\mathrm{B}$の濃度変化が$\mathrm{A}$の濃度変化に比べて無視できるほど小さくなる($\mathrm{A}$に比べて$\mathrm{B}$が無尽蔵に存在する場合)ので、$$[\mathrm{B}]\approx[\mathrm{B}]_{0}$$と近似でき、$(4.2)$式は$$-\dfrac{d[\mathrm{A}]}{dt}=(k[\mathrm{B}]_{0})[\mathrm{A}]\tag{4.11}$$となる。$k[\mathrm{B}]_{0}$は定数であるから新たに$k’$などと置けば、微分方程式は$$-\dfrac{d[\mathrm{A}]}{dt}=k'[\mathrm{A}]\tag{4.12}$$と書き直せて、$\mathrm{A}$の一次反応と全く同様になる。このような反応を特に「擬一次反応」と呼び、濃度$[\mathrm{A}]$は$$[\mathrm{A}]=[\mathrm{A}]_{0}e^{-[\mathrm{B}]_{0}kt}\tag{4.13}$$で近似できる。初濃度の差が指数関数のオーダーで効いてくるため、$[\mathrm{B}]_{0}=10[\mathrm{A}]_{0}$ 程度の差であっても擬一次反応として扱うことができる。
§より複雑な反応の速度論
冒頭でも触れた通り、逐次反応や逆反応を考慮しなければならない系では単純な微分方程式が得られず、解析的に解くことが難しい場合も出てくる。このような場合は反応速度の解析解を厳密に求めるのではなく、定常状態近似などを用いて議論することになる。
次回の記事では逐次反応や逆反応の概念を紹介し、定常状態近似について解説することにする。
(参考文献)
・化学マスター講座「物理化学」丸善株式会社 第1版第1刷
・マッカーリ・サイモン「物理化学(下)分子論的アプローチ」東京化学同人 第1版第9刷

 図1.一次反応のイメージ
図1.一次反応のイメージ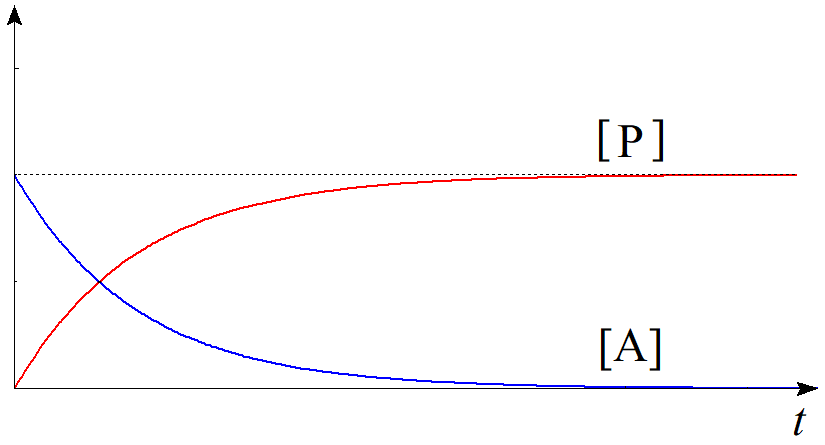 図2.一次反応における濃度の時間変化
図2.一次反応における濃度の時間変化 図3.二次反応のイメージ
図3.二次反応のイメージ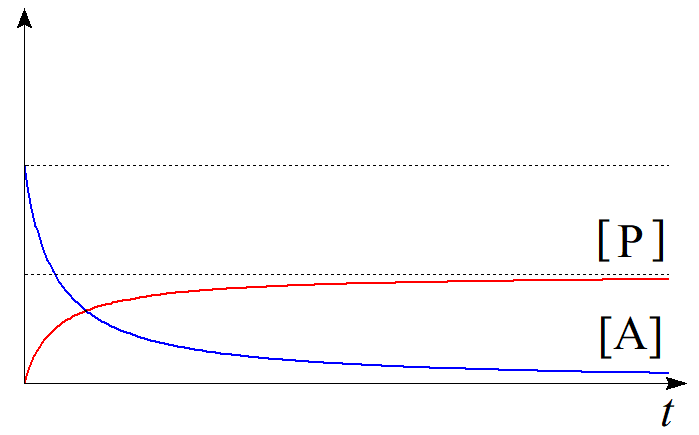 図4.二次反応における濃度の時間変化
図4.二次反応における濃度の時間変化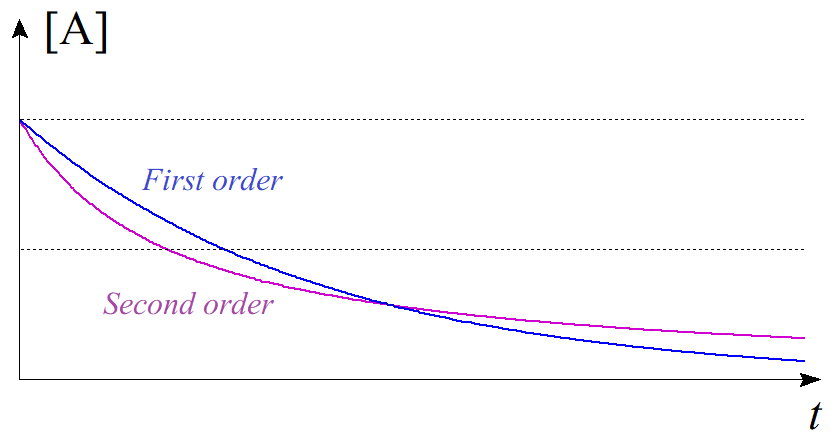 図5.一次反応と二次反応の比較
図5.一次反応と二次反応の比較 図6.一般の二次反応のイメージ
図6.一般の二次反応のイメージ